
glava04
.pdf
Раздел II
МАГНЕТИЗМ
Глава 4
Магнитное поле
§ 33
Магнитное поле и его характеристики
Важнейшей особенностью магнитного поля является то, что оно действует
только на движущиеся в этом поле электрические заряды. Характер взаимодей-
ствия магнитного поля на ток различен в зависимости от формы проводника, по которому течет ток, от расположения проводника и от направления тока.
При исследовании магнетического поля используется замкнутый плоский контур с током,
размеры которого малы по сравнению с расстояниями до токов, образующих магнитное поле. Ориентация контура в пространстве характеризуется направлением нормали к контуру. В качестве положительного направления нормали принимается направление,
связанное с током правилом правого винта.
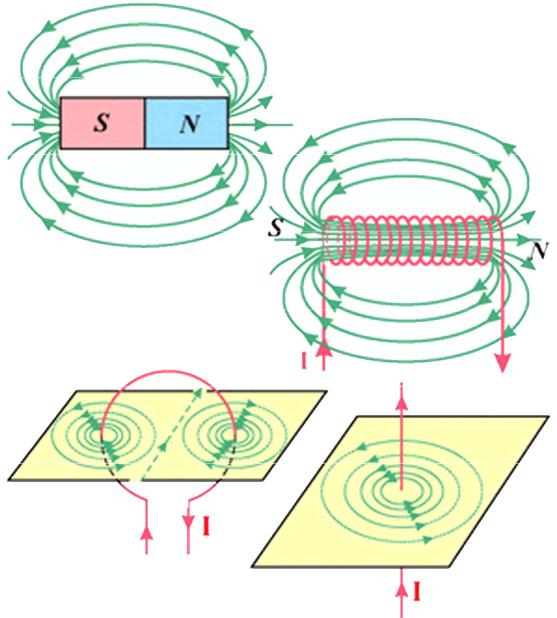
Магнитное поле оказывает на рамку с током ориентирующие действие, поворачивая его определенным образом. Вращающий момент сил, действующий на рамку с током определяется выражением
R |
(33.1) |
M =[pm ×B], |
|
или его величина |
|
M = pmBsin α , |
|
где |
|
pm = ISn |
(33.2) |
магнитный момент рамки с током, |
|
B = Mmax pm – магнитная индукция. |
|
R |
R |
Магнитный момент короткой катушки состоящей из N витков равен pm |
= NISn. |
Магнитная индукция B в данной точке однородного магнитного поля опреде-
ляется максимальным вращающим моментом Mmax , действующим на рамку с магнитным моментом pm , равным единице, когда нормаль к рамке n перпенди-
кулярна направлению поля.
Так как магнитное поле является силовым, то его можно изображать с помощью
линий магнитной индукции.
Магнитное поле макротоков описывается вектором напряженности H .
Для однородной изотропной среды вектор магнитной индукции связан с векто-
ром напряженности следующим соотношением
B = μ0μH . |
(33.3) |

Задача 1. Найдите силу тока в тонком круговом витке, если радиус витка
100 мм, а его магнитный момент 0,06 А×м2.
Дано: |
СИ |
Решение |
R =100 мм |
0,1 м |
Величина вектора магнитный момент тонкого кругового |
p = 0,06 А×м2 |
|
витка с током определяется по формуле |
|
|
p = IS , |
I = ? |
|
|
|
|
|
где S = πR2 – площадь кругового витка. С учетом этого получаем
p = IπR2 .
Из этого равенства выразим силу тока
I = p .
πR2
Подставим в полученное выражение числовые значения
I = |
0,06 А×м2 |
» 1,9 А. |
||
3,14 |
×(0,1м)2 |
|||
|
|
|||
Задача 2. Рамка радиуса 10 см, содержащая 100 витков проволоки, нахо-
дится в магнитном поле с индукцией 0,01 Тл. По виткам течет ток 0,5 А. Опреде-
лите угол, который составляет нормаль рамки с направлением индукции магнит-
ного поля, если на рамку действует вращающий момент 13,6 мН×м.
Дано: |
СИ |
Решение |
R =10 см |
0,1 м |
Величина вращающего момента, |
N =100 |
|
действующая на рамку с током во |
B = 0,01Тл |
|
внешнем магнитном поле, определяется формулой |
I = 0,5 А |
|
M = pmBsin α, |
M =13,6 мН×м |
0,0136 Н×м |
где pm – величина магнитного момента рамки с то- |
|
|
|
a = ? |
|
ком, которая определяется выражением |
|
|
pm = NIS . |
|
|
В этой формуле S = pR2 – площадь поверхности рамки. Выражения для pm и S
подставим в формулу для вращающего момента и получим следующее равенство
M = NIpR2Bsin a .
Из полученной формулы выразим синус угла
sin a = |
M |
|
|
|
||
|
. |
|
|
|
||
pR2NIB |
|
|
|
|||
Подставим числовые значения |
|
|
||||
sin a = |
|
|
0,0136 Н×м |
» 0,866 |
или α = 60°. |
|
|
×(0,1 м)2 |
×100 ×0,5 А×0,01Тл |
||||
3,14 |
|
|
||||
Задача 3. Рамка с площадью поперечного сечения 50 см2 содержит 100
витков проволоки и находится в магнитном поле с индукцией 0,1 Тл. По виткам течет ток 1 А. Определите максимальный вращающий момент, действующий на
рамку.
Дано: |
СИ |
Решение |
|
S = 50 см2 |
0,005 м2 |
Максимальный вращающий момент |
|
N =100 |
|
действует на рамку с током в том случае, |
|
B = 0,1 Тл |
|
когда угол между векторами индукции магнитного поля |
|
I =1 А |
|
R |
|
|
B и магнитного момента рамки pm равен 90°. |
В этом |
|
|
|
|
|
Mmax = ? |
|
случае формула для величины вращающего момента |
|
|
|
имеет вид |
|
Mmax = pmB,
где величина магнитного момента pm рамки с током определяется выражением pm = NIS .
Подставим это равенство в формулу для Mmax
Mmax = NISB.
Рассчитаем числовое значение максимального вращающего момента рамки
Mmax = 100 ×1 А×0,005 м2 ×0,1 Тл = 0,05 Н×м = 50 мН×м .
§ 34
Закон Био-Савара-Лапласа
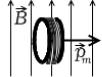
Закон Био-Савара-Лапласа для проводника с током I , элемент dl которого создает в некоторой точке
А создает индукцию поля dB, записывается в виде
R |
|
R |
|
|
||
μ0μ I[dl × r] |
|
|
||||
dB = |
, |
(34.1) |
||||
4π |
r3 |
|
||||
|
|
|
||||
где dl – вектор, по модуля равный длине dl |
элемента |
|||||
проводника и совпадающий по направлению с током; r
– радиус-вектор, проведенный из элемента dl проводника в точку А поля; r –
модуль радиус-вектора r .
Направление dB перпендикулярно dl и r , т.е. перпендикулярно плоско-
сти, в которой они лежат, и совпадает с касательной к линии магнитной индук-
ции. Это направление можно найти по правилу правого винта: направление вращения головки винта дает направление dB, если поступательное движение
винта соответствует направлению тока в элементе.
Модуль вектора dB определяется выражением
dB = |
μ0μ Idlsin α |
, |
(34.2) |
||
4π |
|
||||
r2 |
|||||
|
|
|
|||
где α – угол между векторами dl |
и r . Магнитное поле в точке А, наводимое от |
||||
всего проводника, найдем проинтегрировав выражение (34.2)
B = ∫ dB .
l
Для магнитного поля, как и для электрического справедлив принцип супер-
позиции: вектор магнитной индукции результирующего поля, создаваемого не-
сколькими токами или движущимися зарядами, равен векторной сумме магнит-
ных индукций складываемых полей, создаваемых каждым током или движущим-
ся зарядом в отдельности:
B = ∑Bi . |
(34.3) |
i

1. Магнитное поле прямого тока – тока, текущего по тонкому прямому проводу бесконечной длины. В
произвольной точке А, удаленной от оси проводника на расстояние R , векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей.
В качестве переменной интегрирования выберем угол α, выразив через него все остальные величины. Из рисунка следует, что
r = |
R |
, dl = |
rdα |
|
sin α |
sin α |
|||
|
|
(радиус дуги CD вследствие малостиdl равен r , поэтому угол FDC можно счи-
тать прямым). Подставив эти выражения в (34.2), получим, что магнитная индук-
ция, создаваемая одним элементом проводника, равна
dB = |
μ0μ |
Isin αdα . |
|
|
(34.4) |
|||||
|
|
|
|
|||||||
|
|
4πR |
|
|
|
|
|
|
||
Так как угол α для всех элементов тока изменяется в пределах от 0 до π, то |
||||||||||
согласно (34.3) и (34.4), |
|
|
|
|||||||
B = |
∫dB = |
μ |
μI |
π |
μ |
μ2I |
или |
|||
0 |
|
∫sin αdα = |
0 |
|
||||||
|
|
|
|
|
4π |
0 |
4πR |
|
||
|
|
|
|
|
|
|
|
|
|
|
B = |
μ0μ I |
. |
|
|
|
|
(34.5) |
|||
2π |
R |
|
|
|
|
|||||
Магнитное поле прямого тока конечной длины в точке отстоящей от проводника на расстоянии R можно найти по выражению
B = |
|
dB = |
μ0μI α2 |
sin αdα = |
μ0μI |
− cos α2 ) или |
||
∫ |
4π |
∫ |
(cos α1 |
|||||
|
|
|
|
4πR |
|
|||
|
|
|
|
|
α1 |
|
|
|
B = |
μ0μ I |
(cos α1 |
− cos α2 ) |
|
|
|||
4π |
R |
|
|
|||||
|
|
|
|
|
|
|||
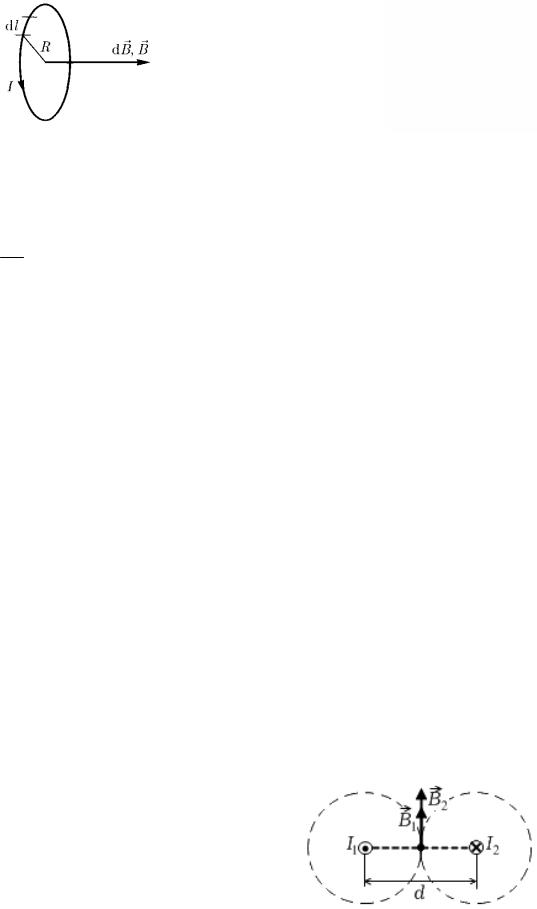
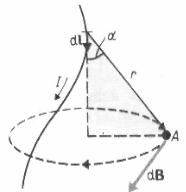
2. Магнитное поле в центре кругового проводника с током. Как следует
из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления – вдоль нормали от витка. Поэтому сложение векторов dB
можно заменить сложением их модулей. Так как все
элементы проводника перпендикулярны радиус-вектору ( sin α = 1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R , то,
согласно (34.2),
dB = μ0μ I dl . 4π R2
Тогда
|
m0m I |
2πR |
|
m0mI |
|
I |
|
|||
B = ∫dB = 4p |
× |
|
∫0 |
dl = |
|
2pR = mm0 |
|
или |
||
R2 |
4pR2 |
2R |
||||||||
B = μμ0 |
I |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2R |
|
|
|
|
|
|
|
|
|
Задача 1. По двум бесконечным параллельным проводам, находящимся на расстоянии 20 см друг от друга, текут в противоположных направлениях токи 10
А каждый. |
Вычислите величину магнитной индукции в точке, расположенной |
|||
посередине между проводами. |
||||
Дано: |
|
СИ |
|
Решение |
|
|
|||
d = 20 см |
|
0,2 м |
|
Как видно из рисунка, вектор магнитной индукции |
I1 = I2 = 10 А |
|
|
каждого из проводников в точке, расположенной между |
|
|
|
|
|
ними, направлен вертикально вверх. По принципу супер- |
B = ? |
|
|
|
|
|
|
|
|
позиции имеем |
B = B1 + B2 . |
|
|
||
С учетом направления векторов B1 и B2 получаем
B = B1 + B2 .
Величины векторов индукции магнитного
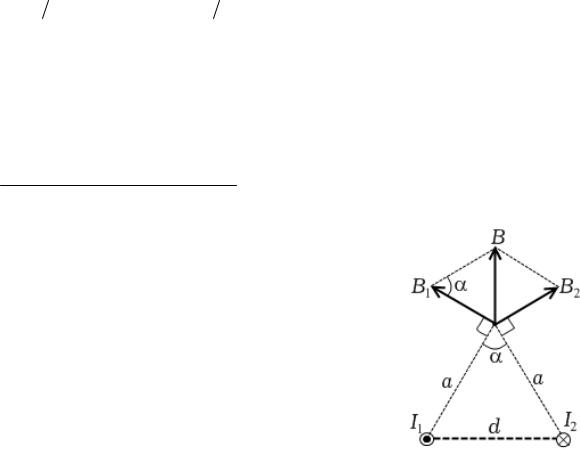
поля от каждого из проводников найдем по формуле (34.5)
B = μ0 |
I1 |
= |
μ0I1 и B = μ0 |
I2 |
= |
μ0I2 . |
|||
|
|
||||||||
1 |
2π d 2 |
πd |
2 |
2π d 2 |
πd |
||||
|
|
|
|
|
|
|
|
||
Тогда суммарная величина магнитной индукции в указанной точке равна
B = μ0I1 + μ0I2 = μ0 (I1 + I2 ) .
πd πd πd
В полученное выражение подставим числовые значения
B = 4 ×3,14 ×10−7 Гн/м×(10 А +10 А) = 4 ×10−5 Тл = 40 мкТл . 3,14 ×0,2 м
Задача 2. По двум бесконечным параллельным
проводам, находящимся на расстоянии 10 см друг от друга, текут в противоположных направлениях токи 5 А
каждый. Вычислите величину магнитной индукции в точке, удаленной от обоих проводов на одинаковое расстояние 10 см.
Дано: |
СИ |
Решение |
d =10 см |
0,1 м |
Индукция магнитного поля проводника I1 в указан- |
a =10 см |
0,1 м |
ной на рисунке точке равна B , а ее направление определя- |
|
|
1 |
I1 = I2 = 5 А |
|
ется по правилу правого винта. Аналогично находим на- |
|
|
|
B = ? |
|
правление индукции B2 проводника I2 . |
|
|
|
Согласно принципу суперпозиции магнитных полей |
||
B = B1 + B2 . |
|
|
|
Величины векторов B1 и B2 определяются выражениями |
|||
B = μ0I1 и B = μ0I2 . |
|||
1 |
2pa |
2 |
2pa |
|
|
||
Из условия задачи следует, что
B1 = B2
Как видно из рисунка и условия задачи, треугольник, в двух вершинах ко-
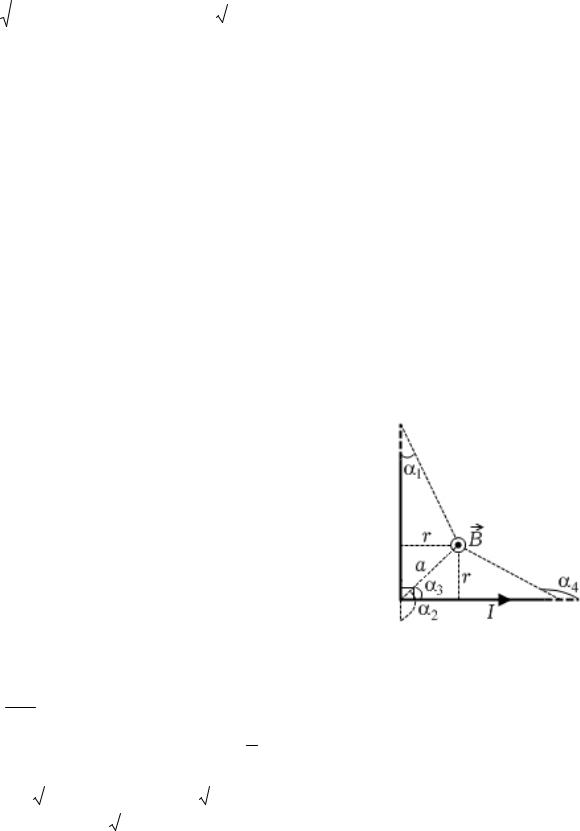
торого лежат проводники I1 и I2 , и треугольник, образованный векторами B1 , B2
и B, являются подобными и равносторонними, т.е.
|
|
|
|
= B = B = |
μ0I1 |
. |
|||||||
B = B2 + B2 − 2B B cos α = B |
|||||||||||||
2 − 2 cos 60° |
|||||||||||||
|
|||||||||||||
|
1 |
2 |
1 |
2 |
1 |
1 |
2 |
2πa |
|||||
|
|
|
|||||||||||
Подставим числовые значения в полученное выражение |
|
|
|
||||||||||
B = |
4 ×3,14 ×10−7 |
Гн/м×5 А |
= 10−5 Тл = 10 мкТл . |
|
|
|
|||||||
2 |
×3,14 ×0,1м |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||
Задача 3. По длинному проводу, согнутому под прямым углом, течет ток 10
А. Найдите магнитную индукцию в точке, лежащей на биссектрисе этого прямого
угла, на расстоянии 5 см от его вершины.
Дано: |
|
СИ |
Решение |
I =10 |
А |
|
Вектор магнитной индукции B в указанной точке с уче- |
a = 5 см |
0,05 м |
том направления силы тока в проводнике направлен перпен- |
|
|
|
|
|
B = ? |
|
|
дикулярно плоскости рисунка на нас. |
|
|
|
|
Для нахождения величины индукции магнитного
поля B разобьем проводник на два прямолинейных участка в точке изгиба. Тогда величина магнитной индукции может быть найдена по принципу суперпозиции
B = B1 + B2 .
Величина поля от первого участка определяется
выражением
B1 = μp0I (cos a1 - cos a2 ) , 4 r
где α1 = 0 , α2 =135° и r = asin 45° = a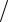

 2 . С учетом этого получаем
2 . С учетом этого получаем
B = m0I |
2 |
(1- (- |
1 |
)) = m0I( |
2 |
+1) . |
||
|
|
|
||||||
1 |
4pa |
2 |
4pa |
|||||
|
||||||||
Величина поля от второго участка проводника определяется формулой
B2 = μp0I (cos a3 - cos a4 ) , 4 r
где α3 = 45° и α4 = 180° . С учетом этого получаем
|
= |
μ0I |
2 |
1 |
|
− (−1)) = |
μ0I( |
2 |
+1) |
||
B2 |
4πa |
( |
|
|
|
. |
|||||
|
|
|
|||||||||
|
|||||||||||
|
|
2 |
|
|
4πa |
||||||
В результате подстановки выражений для B1 и B2 в первую формулу для
B получим
B= μ0I(
 2 +1) . 2πa
2 +1) . 2πa
Вполученную формулу подставим числовые значения
B= 4 ×3,14 ×10−7 Гн/м×10 А×(
 2 +1) » 9,7 ×10−5 Тл = 97 мкТл .
2 +1) » 9,7 ×10−5 Тл = 97 мкТл .
×3,14 ×0,05 м
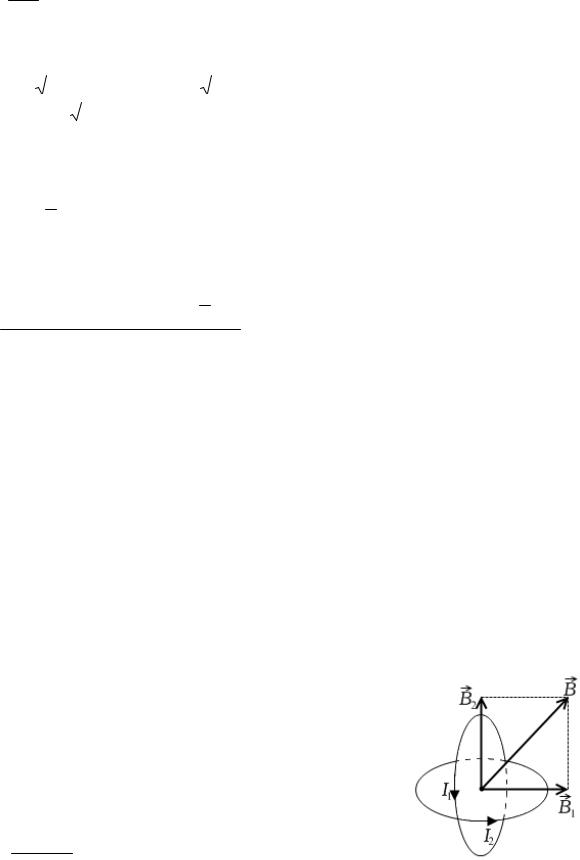
Задача 4. Два круговых витка расположены в двух взаимно-
перпендикулярных плоскостях так, что центры этих витков совпадают. Радиус каждого витка 5 см, по ним текут одинаковые токи 10 A. Найдите магнитную ин-
дукцию в центре витков.
Дано: |
СИ |
|
Решение |
R = 5 см |
0,05 м |
Как видно из рисунка, виток, по которому течет ток |
|
I1 = I2 = 10 А |
|
I , в центре наводит магнитное поле индукцией B , а ви- |
|
|
|
1 |
1 |
|
|
|
|
B = ? |
|
ток с током I2 – |
поле индукцией B2 . Направления этих |
|
|
||
|
|
|
|
векторов определяются по правилу правого винта. Тогда суммарное магнитное поле в центре витков определим по принципу суперпозиции
B = B1 + B2 .
Величину вектора B найдем по теореме Пифагора
B = 
 B12 + B22 ,
B12 + B22 ,
где величины векторов B1 и B2 определяются по формулам
