Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ухтинский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

часть 1

.pdf

Скачиваний:

Добавлен:

02.03.2016

Размер:

545.64 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

Знак «+» подтверждает, что на этом участке газ получает количество теплоты.

Газ получает количество теплоты Q1 всего:

Q	i	V		P P i 2			P V			V		20 56 76 103	( Дж) .
Q		V	2	P P i 2			P V		3	V	2	20 56 76 103	( Дж) .
1	2		2	2	1	2	2		3		2
	2					2
2. Газ отдаёт количество теплоты								Q		охладителю на 2х участках: Q				на
									2				34

участке 3→4 (изохорный процесс) и Q41 4→1 (изобарный процесс), т.е.:

Q2 Q34 Q41 .

Количество теплоты, отданное газом на участке 3→4:

T T

R T

Q mc Т m

2 M

V P

P P

3 2

учтён закон Шарля:

, формула (3) и что

P P .

Подставим численные значения:

Q34 52 3 4 103 30 103 ( Дж) ,

знак «–» подтверждает, что на этом участке газ отдаёт количество теплоты.

Количество теплоты, отданное газом на участке 4→1:

Q mc T		T i 2 R T T ,
41	P 1	4	2	1 4
			2

учтём формулу (1), распишем T4 , применим формулу (3) и что P4 P1 и

P2 P3 :

	i 2			P V P				i 2			P V P V P					i 2
Q				1 1		4							1 1	1	3 2			P V V ,
Q			R				T			R								P V V ,
41		2					3		2						R		2		1 1 3
		2			R P				2			R P			R		2
						3								3
Подставим численные значения:
Q41		7	12 103 1 42 103							( Дж) .
		2

Знак «–» подтверждает, что на этом участке газ отдаёт количество теплоты.

Газ отдаёт количество теплоты Q2 охладителю всего:

Q		i	V	P P			i 2	P V V			30 42 72 103	( Дж) .
		2
	2		3	4		2	2	1	1	3
Знак			«–»		не		интересует,		он	уже учтён, важен		модуль, т.е.

Q2 72 103 Дж .

3. Работа замкнутого цикла вычисляется как разница между полученным и отданным теплом (можно каждый участок рассмотреть в отдельности, т о- гда работа цикла будет равна алгебраической сумме работ участков):

A Q1 Q2 .

Подставим численные значения: А 76 72 4 103 ( Дж) .

4. Термический КПД любого цикла:

Q1 Q2 A .

Q1 Q1

Подставим численные значения:

764 0,0526 5,26% .

Ответ: Q1 76кДж, Q2 72кДж, А 4кДж, 5,26% .

Рекомендуемое задание № 3

Идеальный газ, совершающий цикл Карно, 23 количества теплоты Q1 , полу-

ченного от нагревателя, отдаёт охладителю. Температура T2 охладителя равна 280К . Определить температуру T1 нагревателя.

Дано:		СИ:	Решение:
Дано:		СИ:	Решение:
Q2	2		P	1 Q1
	2			1 Q1
	3 Q1			2
T2	280К			2
T2	280К			4
T1	?			4
T1	?			Q2 3

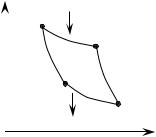
Цикл Карно (рис.2): рис.2

1→2 – изотермическое расширение 3→4 – изотермическое сжатие 2→3 – адиабатное расширение 4→1 – адиабатное сжатие

КПД цикла Карно представим двояко – через количество теплоты и температуры:

Q1	Q2	1		Q2
		1
	Q1			Q1
	Q1			Q1	.
T1	T2		T2		.
T1	T2	1	T2
		1
T1			T1
T1			T1

Приравняем правые части:

1 Q2	1 T2	Q2	T2	,
Q	T	Q	T
1	1	1	1

тогда температура нагревателя:

T	Q1	T	Q1 T2		3	T .
	Q2		2		2
1		2		Q1		2
			3

Подставим численные значения: T1 32 280 420(K).

Ответ: T1 420K.

Рекомендуемое задание № 4

Газ совершает цикл Карно. Абсолютная температура нагревателя в 3 раза выше, чем температура охладителя. Нагреватель передал газу Q1 41,9кДж теплоты. Какую работу совершил газ?

Дано:

Си:

Решение:

Q1 41,9кДж

41,9 103 Дж

КПД цикла Карно представим двояко –

T1 3T2

через количество теплоты и температуры:

A ?

T1 T2

Приравняем правые части:

тогда работа совершённая газом:

Q .

Подставим численные значения:

2 41,9 103

27,93 103 ( Дж).

Ответ: А 27,93кДж.

Рекомендуемое задание № 5

Идеальный газ совершает цикл Карно. Температура T1 нагревателя равна 470К , температура T2 охладителя равна 280К . При изотермическом расширении газ совершает работу A 100 Дж . Определить термический к.п.д. цикла, а также количество теплоты Q2 , которое газ отдает охладителю при изотермическом сжатии.

	Дано:	СИ:	Решение:
	Дано:	СИ:	Решение:
T1	470К		P	1 Q1
T2	280К			1 Q1
T2	280К			2
A12 100 Дж				2
A12 100 Дж				4

1.	?
1.	?			Q2 3
2.	Q2 ?			Q2 3
2.	Q2 ?
				рис.3	V
					V

Цикл Карно (рис.3):

1. КПД цикла Карно:

T1 T2 .

Подставим численные значения:

470 280 0,404 4,04% . 470

2.1й способ. Процесс 3→4 – изотермическое сжатие, т.е. изменение внутренней энергии U 0 , тогда количество теплоты полученное:

Q1 Q12 A12 U A12 .

КПД цикла Карно, с учётом выше написанного:

1 Q2 1 Q2 ,

Q1 A12

тогда количество теплоты, отданное охладителю:

Q2 1 A12 . Подставим численные значения:

Q2 (1 0,404) 100 59,6( Дж) .

2й способ. КПД цикла Карно:

1 Q2 1 T2 ,

Q1 T1

тогда количество теплоты, отданное охладителю:

Q	2	T2	Q	T2	A .

		T1	1	T1	12

Подставим численные значения: Q2 280470 100 59,6( Дж).

Ответ: 0,404, Q2 59,6 Дж.

Рекомендуемое задание № 6

Идеальный газ совершает цикл Карно. Работа A1 изотермического расширения газа равна 5 Дж . Определить работу A2 изотермического сжатия, если термический к.п.д. цикла равен 0,2 .

Дано:

СИ:

Решение:

A1 A12

5 Дж

КПД Цикла Карно:

0,2

A34 A2

учли, что при изотермическом расширении всё

тепло идёт на совершение работы, т.е. Q1

A1 и Q2

(см. задача 5, с.74).

Отсюда работа при изотермическом сжатии:

A2 1 A1 . Подставим численные значения:

А2 1 0,2 5 4( Дж).

Ответ: А2 4 Дж.

Рекомендуемое задание № 7

Кислород массой m 2кг увеличил свой объём в n 5 раз один раз изотермически, другой - адиабатически. Найти изменения энтропии в каждом из указанных процессов.

		Дано:		СИ:	Решение:
		Дано:		СИ:	Решение:
m 2кг					Изменение энтропии выражается общей фор-
	32 10 3		кг		мулой:
			моль		S1 S2 S1			2	dQ .
V2		n 5			S1 S2 S1				dQ .
V2		n 5						1	T
								1
					1. Изотермический процесс.
	V				1. Изотермический процесс.
1					1й способ. Вынесем за знак интеграла посто-
1.		T const			1й способ. Вынесем за знак интеграла посто-
2.		Q 0			янную величину – температуру:
						1	2 dQ Q .
Si ?					S	1
Si ?					S
					T 1			T
					T 1			T

Первое начало термодинамики для конечного состояния системы, с учётом того, что изменение внутренней энергии равно нулю:

Q U A A PdV m R T M V

2й способ.

S1 2	m	R dV	m	R lnV2 .
	M		M
1		V		V1

Подставим численные значения:

dV m R T lnV2 .

M V1

		2 8,31								3				Дж
S1						ln5		0,5194 10			1,609	835,9	836		.
S1		32 10 3				ln5		0,5194 10			1,609	835,9	836	К	.
		32 10 3												К
2. Адиабатический процесс ( dQ 0 ). Изменение энтропии:
S2	1		dQ		0		0.
S2	1		dQ				0.
		1	T	T
Ответ: S1				836				Дж ,	S2 0..
								К

Рекомендуемое задание № 8

Найти изменение S энтропии при изобарическом расширении азота ма ссой m 4г от объёма V1 5л до объёма V2 9л .

Дано:		Си:
P const
m 4г		4 10 3 кг
28 10 3	кг
28 10 3	моль
	моль
i 5
V1 5л		5 10 3 м3
V2 9л		9 10 3 м3
S ?

Решение:

Изменение энтропии:

S 2 dQP i 2				m
S 2 dQP i 2				M
	1	T	2	M
	i 2	m	R ln T2 .
	2	M	R ln T2 .
	2	M	T
			1

R 2 dT

1 T

Учли, что элементарное количество теплоты при постоянном давлении:

dQP m cP dT	i 2	m	R dT ,
	2	M

а удельная теплоёмкость при постоянном да влении:

cP	i 2	R	.
	2
		M

Используя закон Гей-Люссака найдём отношение конечной и начальной те м- ператур:

V1	V2	T2	V2	,
T	T	T	V
1	2	1	1

тогда изменение энтропии:

S	i 2	m	R ln	V2	.
S	2	M	R ln	V	.
	2	M		V
				1

Подставим численные значения:

S	5 2	4 10 3	8,31	ln	9 10 3	7	1	8,31 ln	9	8,31	ln1,8
	2	28 10 3			5 10 3	2	7		5	2

4,155 0,588 2,44 Дж .

Ответ: S 2,44 ДжК .

Рекомендуемое задание № 9
Найти изменение S энтропии при превращении массы	m 10г льда
(t 200 C ) в пар (tп 1000 C ).

	Дано:				Си:
m 10г					10 2 кг
t	200 C				253К
1
t2	00 C				273К
t3	1000 C				373К
cлёд 2100				Дж
cлёд 2100		кг К
		кг К
335 103				Дж
				кг
cвода 4200				Дж
cвода 4200			кг К
			кг К
r 2,26 106				Дж
				кг
S ?

Решение:

Изменение энтропии состоит из сумм изменений энтропии: 1 – нагрев льда, 2 – плавление льда, 3 – нагрев воды, 4 – испарение воды.

S Sледнагр Sледплав Sводанагр Sводаисп .

Изменение энтропии при нагреве льда:

2	dQ	T2	dT		T
Sледнагр	T	m c	T	m cльда ln	2	.

1		T1			T
					1

Подставим численные значения:

S нагр 10 2	2100 ln 273	1,6	Дж .
лед	253		К
	253		К

Изменение энтропии при плавлении льда:

плав	2	dQ	Qплав	m
S лед	1				,
		T	T	T2

где – удельная теплота плавления. Подставим численные значения:

S	плав	10 2	335 103		Дж	.
S	лед			12,271		.
	лед		273		К
			273		К

Изменение энтропии при нагреве воды:

нагр	T3	dT		T3
Sвода	m c		m cводы ln		.
Sвода	m c	T	m cводы ln	T	.
	T2	T		T
				2

Подставим численные значения:

S нагр 10 2	4200 ln 373	13,11	Дж .
вода	273		К
	273		К

Изменение энтропии при испарении воды:

исп 2	dQ	Qпар	mr
Sвода				,
Sвода	T	T	T3	,
2	T	T	T3
2

где r – удельная теплота испарения. Подставим численные значения:

исп	10 2 2,26 106		Дж
Sвода	373	60,59	К	.
	373		К

Тогда изменение энтропии всего:

S 1,6 12,27 13,11 60,59 87,58 88

Дж .

Ответ: S 88 Дж .

Рекомендуемое задание № 10

Найти изменение

энтропии при изотермическом расширении массы

m 6г водорода от давления P1

100кПа до давления P2

50кПа .

Дано:

Си:

Решение:

m 6г

6 10 3 кг

Изменение энтропии при изотермическом процес-

T const

се:

2 10 3 кг

dQ .

100кПа

Па

50кПа

5 10

Па

Первое начало термодинамики для конечно-

го состояния системы, с учётом того, что измен е-

S ?

ние внутренней энергии равно нулю и давление

выразим из уравнения Менделеева - Клапейрона:

Q U A A PdV

R T

R T ln

Применим закон Бойля-Мариотта и выразим отношение объёмов:

P V P V

тогда изменение энтропии:

R Т

R ln

Подставим численные значения:

6 10 3

8,31 ln 2 3 8,31 0,693 17,28 17,3

Дж .

2 10 3

Ответ: S 17,3

Дж .

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.03.2016644.61 Кб77Христорождественская UNIT1.doc
#
02.03.201652.26 Кб18художественное конструирование заочка.docx
#
19.07.201958.37 Кб5Ценообразование.doc
#
01.04.20251 Mб0Ч6.docx
#
01.04.2025107.49 Кб1Часть 1(1 вариант) .docx
#
02.03.2016545.64 Кб67часть 1.pdf
#
02.03.2016463.44 Кб45часть 2.pdf
#
01.04.2025210.94 Кб0часть 4.1..doc
#
01.04.2025292.86 Кб0Часть 5.doc
#
01.04.2025828.42 Кб2Часть 5.doc
#
01.04.2025101.38 Кб1Часть 6.doc