5.Сполучення.

Означення. Сполученням з n елементів по m елементів називають будь-яку m-елементну підмножину n-елементної множини.

Звідси випливає, що сполучення з n елементів по m елементів - це всі m-елементні підмножини n-елементної множини, причому різними підмножинами вважаються ті, склад яких відрізняється хоч би одним елементом. Підмножини, які відрізняються між собою лише порядком слідування елементів, не є різними. Отже, комбінації на відміну від розміщень, - це невпорядковані підмно­жини даної множини.

Кількість всіх сполучень з n елементів по m елементів поз­начають символом 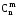(читають: "число комбінацій зn по m" або "це із n по m). С - перша буква французького слова combinasion - комбінація. Для сполучень mn.

Для обчислення числа сполучень з n елементів по m елемен­тів існує декілька формул.

Теорема 5. Для довільних натуральних n i m (mn) має місце формула

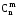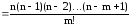= (1)

Доведення. Спочатку утворимо всі можливі неупорядковані m-елементні підмножини n-елементної множини, їх число дорівнює 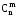. Потім з кожної одержаноїm-елементної підмножини перестанов­кою її елементів одержимо всі упорядковані m-елементні підмножи­ни, яких буде у m! раз більше, бо кожну m-елементну підмножину можна упорядкувати m! способами. Отже, дістанемо

=m!,

а звідси =

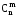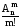
Цю теорему можна довести іншими способами, зокрема методом мате­матичної індукції.

Формулу (1) для числа комбінацій можна записати в іншому вигляді. Якщо чисельник і знаменник її помножити на (n-m)!, то дістанемо:

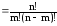(2)

Число 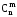має ряд цікавихi важливих у практичних застосу­ваннях властивостей, які подамо у вигляді теорем.

Теорема 6. Для довільних натуральних n і m (mn) справджує­ться рівність

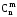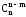=(3)

Доведення. Рівність (3) безпосередньо випливає з формули (2). Справді,

=

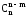
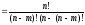
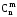
Теорема 7. Для довільних натуральних m i n (mn) справджу­ється рівність

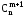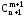+ = (4)

Доведення. Використаємо формулу (2):

++=

==

=.

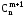
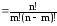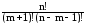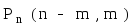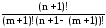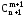Наслідок 1. Формулу (4) при розв'язуванні задач зручно ін­коли використовувати в такому вигляді:

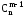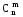+ =, (5)

яка є наслідком формули (4).

Формулу (5) називають ще формулою Паскаля.

Наслідок 2. Число комбінацій з nелементів по m елементів виражаєть­ся через: а) число розміщень в n елементів по m елементів форму­лою

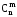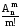=-наслідок з (1);

б) число перестановок формулою

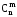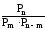=- наслідок з (2).

Наслідок 3. Нехай множина М складається з двох елементів а і b. Тоді число перестановок з n елементів, в яких елемент а повторюється n-m разів, а елемент b повторюється m разів, дорівнює

=.

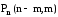
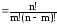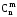Отже, число комбінацій з n елементів по m дорівнює числу перестановок з повтореннями складу (n-m,m).

Приклад.1. Скількома способами можна вибрати з 20 осіб делегацію в складі 4 осіб?

Розв'язання. Різними вважатимемо ті делегації, які відрізняються хоча б одним членом. Кількість способів вибрати з 20 осіб делегацію в складі 4 осіб дорівнює числу комбінацій з 20 елементів по 4:

=

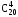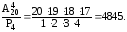
Відповідь. 4845.

Приклад. Скількома способами збори акціонерів з 100 осіб можуть обрати президію з 5 осіб, у тому числі голову і секретаря?

Роз’язання:

1 спосіб. Кількість способів обрання голови і секретаря з 100 осіб дорівнює числу розміщень з 100 по 2 без повторень, тобто:

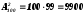
Кількість способів обрання ще трьох членів президії дорівнює числу сполучень з 98 осіб по три, тобто:

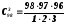
Всього кількість способів обрання президії дорівнює добутку

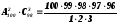
2 спосіб. Кількість способів обрання президії з 5 осіб на зборах, де присутні100, осіб дорівнює числу сполучень з 100 по 5 без повторень, тобто:

Потім президія з 5 осіб обирає з свого складу голову і секретаря. Кількість способів обрання голови і секретаря з 5 осіб дорівнює числу розміщень з 5 по 2 без повторень, тобто:

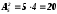
Всього кількість способів обрання президії дорівнює добутку

Відповідь.

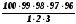
Означення. Сполученням з повтореннями з n елементів по m елементів називається будь-який m-елементний набір виду (а₁,а₂,…,а_m), де кожний з елементів а₁,а₂,…,а_m належить до одного з n типів.

З означення випливає, що сполучення з повтореннями є не впо-рядкованими множинами, тому розташування елементів в набо­рах-множинах не має значення. Різні комбінації з повтореннями відрізняються одна від одної елементами, що до них входять, при цьому кожний елемент може входити в комбінацію декілька разів. Тому для сполучень з повтореннями може бути як m n, так i n<m, на відміну від сполучень без повторень, де завжди mп.

Наприклад, з двох елементів а і b можна скласти такі комбі­нації з повтореннями з двох елементів по три елементи (n<m):

ааa, ааb, bbа, bbb,

а з трьох елементів а, b, с по два елементи (n>m) такі:

аа, аb, ас, bb, bс, сс.

Оскільки комбінації з повтореннями є неупорядкованими мно­жинами, то кожна така комбінація однозначно визначається тим, скільки елементів кожного типу в неї входить.

Наприклад, якщо маємо елементи трьох сортів, то комбінація з повтореннями з трьох елементів по п'ять елементів повністю визначається, якщо вказано, що вона містить два елементи першого типу, не містить жодного елемента другого типу і містить три елементи третього типу. Таку комбінацію можна умовно записати так (2,0,3); з цього запису видно, скільки елементів кожного ти­пу входить в дану комбінацію. Запис іншої комбінації (1,2,2) по­казує, що в цю комбінацію входить один елемент першого типу і по два елементи другого і третього типів. Відмітимо, що в даному випадку кожна комбінація складається з п'яти елементів, що є су­мою всіх елементів, що входять у комбінацію.

Кількість усіх комбінацій з n елементів по m елементів з повтореннями будемо позначати символом 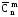. Для його знаходження користуються такою теоремою.

Теорема 8. Число різних можливих сполучень з повтореннями і з n елементів по m елементів при довільних натуральних n іm об­числюється за формулою

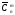
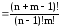(1)

Доведення. Сполучення з повтореннями з n елементів по m елементів можна записати, користуючись тільки цифрами 0 і 1. Це можна зробити так: спочатку запишемо стільки одиниць, скільки елементів першого типу входить у комбінацію, потім напишемо нуль, після нього напишемо стільки одиниць, скільки елементів другого типу входить у комбінацію, потім знову нуль і т.д., тоб­то нуль ставиться між двома групами одиниць елементів двох різних типів. Якщо елементи якого не будь типу зовсім не входять у дану комбінацію, то пишемо підряд два нулі. Наприклад, якщо розгляда­ються комбінації з чотирьох елементів а, b, с, d по шість, то запис (100110111) відповідає такій комбінації {а,с,с,d,d,d}, а запис (110111001) зображує таку комбінацію {а,c,c,d,d,d}.

Впорядкована множина, складена з одиниць і нулів, відповід­на сполученню з повтореннями з n елементів по m елементів, буде мати рівно m одиниць і n-1 нулів, бо кількість одиниць дорівнює числу елементів у сполученні, а число нулів на одиницю менше числа типів елементів, оскільки нуль вживається лише для розділення типів елементів. Тому мiж так утвореними впорядкованими множинами з нулів та одиниць i сполученнями з повтореннями вста­новлюється взаємно однозначна відповідність. Але оскільки кожна така впорядкована множина складається з m одиниць і n-1 нулів,. то кількість усіх сполучень з повтореннями з n елементів по m елементів дорівнюй кількості різних способів упорядкування (n+m-1)-елементної множини, що містить m одиниць і n-1 нулів, тобто

==

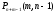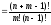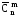
Наслідок. Якщо зіставити одержану формулу з формулою сполучень без повторень з n+m-1 елементів по n-1 елементу, тобто з формулою

=

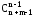
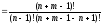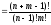
то побачимо, що праві частини цих формул однакові, тому

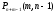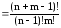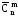==== (2)

Отже, число сполучень з повтореннями з n елементів по m елементів дорівнює числу сполучень без повторень з n+m-1 елементів по n-1 елементів.

Приклад 1. У поштовому відділенні продаються листівки 8 різних видів. Скількома способами можна купити в ньому 10 листівок?

Розв'язання. Оскільки порядок покупки листівок не істотний, а купити їх не можна всі різними (10>8), то маємо сполучення з повтореннями з 8 елементів по 10 елементів. Число їх дорівнює

=

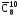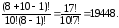
Відповідь. 19448.

Приклад 2.Шість пасажирів сідають на вокзалі в електропотяг, який складається з5 вагонів. Скільки можливих способів посадки пасажирів у вагони, якщо істотним є лише кількість пасажирів?

Розв’язання. Тут маємо сполучення з повтореннями з 5 елементів по 6. Число їх дорівнює

=

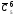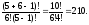
Відповідь. 210.

Схема розвязання комбінаторних задач