4. Перестановки.

Означення. Перестановками з n елементів називаються розмі­щення з n елементів по n елементів.

Перестановки є окремим ви­падком розміщень. Оскільки перестановка містить всі n елементів множини, то різні перестановки відрізняються одна від другої тільки порядком елементів. Можна сказати, що перестановка - це кількість різних способів, якими можна упорядкувати n елементну множину.

Число перестановок з n елементів позначають символом Р_n (Р - перша буква французького слова реrmutation - перестановка).

Оскільки за означенням Р_n =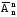,то формули для обчислення числа перестановок з n елементів можна безпосередньо одержати а форму­ли числа розміщень з n елементів по m елементів, замінивши в них m на n:

Р_n =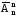=n(n-1)(n-2)…321=n!

або Р_n =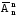= 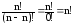(1)

Отже, справедлива теорема

Теорема 3. Число перестановок з n елементів дорівнює добутку всіх натуральних чисел від 1 до n:

Р_n=123 … (n-1)n=n!

Звідси маємо, що у множині, яка містить n елементів, вста­новити певний порядок слідування елементів, тобто упорядкувати n-елементну множину можна n! способами.

Теорему 3 можна довести незалежно від розміщення. Розглянемо всі можливі перестановки з n елементів і полічимо, скільки в них на першому місці один i той же елемент. Якщо поставити названий елемент перед кожною перестановкою а інших елементів, то одержи­мо всі можливі перестановки, які починаються з даного елемента. Отже, число всіх перестановок з n елементів, які починаються з даного елемента, дорівнює Р_n-1. Але тоді число всіх перестановок з n елементів буде дорівнювати

Р_n= n Р_n-1, (2)

бо кожний з n елементів може бути першим.

Користуючись формулою (2), можна далі довести теорему 3 ме­тодом математичної індукції.

1) формула (1) вірна при n=1, бо один елемент може знаходи­тись лише на першому місці, тобто Р₁=1.

2) Припустимо, що формула (1) вірна при n=k, тобто, що

Р_k = k! =12 … k

3) Доведемо, що формула (1) вірна тоді і при n=k+1, тобто, що Р_k+1 = (k+1)! =123 … k(k+1).

Дійсно, за формулою (2)

Р_k+1 = (k+1) Р_k =12 … k(k+1).

4) На основі принципу математичної індукції випливає, що формула (1) вірна для будь-якого натурального значення числа n.

Приклад 1. Скількома способами можна поставити на полиці 6 різних книг?

Розв'язання. Число таких способів дорівнює числу перестановок з шести елементів без повторення, тобто

Р₆ = 12 3 4 5 6 = 720 (способами).

Відповідь. 720.

Приклад 2. Скількома способами можна розташувати пшеницю, жито, овес і ячмінь на чотирьох полях?

Розв’язання. Число таких способів дорівнює числу перестановок з чотирьох елементів без повторення.

Р = 12 3 4 = 24

Відповідь.24 способа.

У розглянутих перестановках без повторення число перестановок з n елементів дорівнює n!. Але якщо серед даних n елементів є однакові, то перестановки , які утворюються одна з одної переставленням однакових елементів, нічим не відрізняються; том цьому випадку кількість різних перестановок буде меншою ніж n!

Означення. Кожний упорядкований n-елементний набір з елементів множини М=(а₁,а₂,…,а_k), - в якому елемент а₁ повторюється n₁ раз, елемент а₂ повторюється n₂ раз, i т.д., елемент а_k повторюється n_k раз, причому n₁+n₂+…+n_k= n називається перестановкою з повтореннями з n nелементів.

Кількість усіх перестановок з повтореннями з n елементів, які відповідають означенню, позначають символом

Р_n(n₁,n₂,…, n_k),

де 1kn.

Теорема 4. Число Р_n(n₁,n₂,…, n_k),всіх перестановок довжи­ною n=n₁+n₂+…+n_k з повтореннями з елементів а₁,а₂,…,а_k, які повторюються відповідно n₁,n₂,…, n_k раз, обчислюється за форму­лою

Р_n(n₁,n₂,…, n_k) = 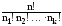(3)

Доведення. Кожна з перестановок містить n елементів. Якби всі елементи були різними, то мали б Р_n=n!. Але оскільки не всі елементи різні, то ряд перестановок будуть однаковими. Зокрема без зміни елементи а₁ можна переставляти між собою n₁! способа­ми, елемент а₂=n₂! способами і т.д,, елемент а_k=n_k! способами. Тому за правилом добутку в кожній перестановці з повтореннями можна переставляти елементи , не змінюючи перестановки n₁!n₂! … n_k! способами. Отже,

Р_n(n₁,n₂,…, n_k) n₁!n₂! … n_k!=n!,

а звідси

Р_n(n₁,n₂,…, n_k) =

Приклад 1. Абонент пам'ятає, що потрібний йому шестицифровий но­мер телефону починається з цифри 3 і містить три п'ятірки і дві дев'ятки. Проте розташування цифр він не пам'ятає. Скільки спроб повинен вробити абонент, щоб набрати потрібний номер?

Розв'язання. Маємо перестановки з повтореннями, всього спроб

буде

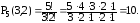
Відповідь. 10.

Приклад 2. Скількома способами можна розділити 10 акцій одного підприємства і 15 акцій іншого між п’ятьма особами?

Розв’язання. Використаємо метод перегородок. Спочатку з’ясуємо, скількома способами можна розділити 10 акцій одного підприємства між п’ятьма особами. Для цього добавимо до 10 акцій 4 перегородки, і розглянемо всі 14 елементів: 10 акцій і 4 перегородки. Кожній такій перестановці відповідає свій спосіб розподілу: перша особа отримує акції, що попали від початку зліва до першої перегородки, і друга – всі акції, що є між першою і другою перегородками і так далі. Отже, кількість розподілів 10 акцій між п’ятьма особами дорівнює числу перестановок з 14 елементів з повтореннями, тобто

Аналогічно, кількість способів розподілу 15 акцій іншого підприємства між п’ятьма особами дорівнює числу перестановок з 19 елементів з повтореннями (15 акцій і 4перегородки), тобто

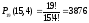
Тоді за правилом добутку, оскільки кожний з розподілів акцій першого підприємства можна комбінувати з кожним способом розподілу акцій двох підприємств між п’ятьма особами буде дорівнювати

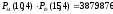
Відповідь. 3879876 способів.