3. Розміщення

Означення. Кожна упорядкована m-елементна підмножина n-елементної множини, називається розміщенням з n елементів по m еле­ментів.

З означення випливає, що nm0 і що розміщення з n елемен­тів по m елементів - це всі m-елементні підмножини, які відріз­няються між собою або складом елементів або порядком їх сліду­вання.

У комбінаторних задачах необхідно вміти підраховувати число всіх розміщень з n елементів по m елементів.

Для позначення числа розміщень з n елементів по m елементів вживають спеціальний символ 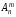(читається: "число розміщень зn по m" або "А із n по m"). А - перша буква французького слова аrrangement, що означає в перекладі розміщення, зведення до поря­дку.

Зрозуміло, що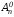=1, бо існує лише одна підмножина n-елементної множини, яка не містить елементів (порожня множина). У загальному випадку має місце таке твердження.

Теорема 1. Число розміщень з n елементів по m елементів до­рівнює добутку m послідовних натуральних чисел від n до n-m+1 включно, тобто

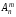= n(n-1) (n-2) … (n-m+1), m>0 (1)

Доведення. Число розміщень з n елементів по m елементів до­рівнює числу всіх m-елементних упорядкованих підмножин n-елементної множини. Перший елемент підмножини можна вибрати n спо­собами. Другий елемент підмножини можна вибрати n-1 способами, оскільки другим елементом можна взяти будь-який елемент множини, крім уже вибраного першим. Кожний із способів вибору першого елемента може об'єднуватись з кожним із способів вибору другого, тому існує n(n-1) способів вибору перших двох елементів для n-елементної упорядкованої підмножини.

Після вибору перших двох елементів залишається n-2 можли­востей вибору третього елемента, і знову, як і раніше, кожна а цих можливостей може комбінуватись з будь-якою із можливостей вибору перших двох елементів, тобто вибір перших трьох елементів можна здійснити n(n-1)(n-2) способами і т.д.

Останній m-й елемент m-елементної упорядкованої підмножини n-елементної множини можна вибрати n-m+1 способом, оскільки до вибору m-го елемента залишилось n-(m-1) елементів.

Отже, число розміщень з n елементів по m елементів дорівнює

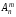= n(n-1) (n-2) … (n-m+1),

що й треба довести.

Цю теорему можна довести Іншими способами, зокрема методом математичної індукції.

Формулу (1) можна записати в іншому вигляді, використовуючи поняття n-факторіала. Дійсно, домножимо і розділимо добуток, що стоїть у правій частині формули (1), на (n-m)!

Дістанемо

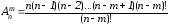
або 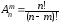(2)

Формула (2) має деякі переваги перед формулою (1) у практичному використанні.

Формула (1) виводилась у припущенні, що m>0, а формулою (2) мож­на користуватись і при m=0, оскільки вона і в цьому випадку дає вірний результат:

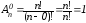
Нагадаємо, що 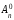=1, а порожня множина є єдиною підмножиною будь-якої множини.

При виведенні формули (1) також припускалось, що n0, тоб­то, що дана множина не порожня. Якщо n=0, то розглядається по­рожня множина. Оскільки порожня множина має тільки одну підмножину (саму себе), то

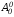=1

Враховуючи, що 0!=1, то формула (2) дає вірний результат і при n=0:

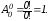
Приклад 1. Розклад одного дня містить 5 різних пар. Знайти кількість можливих розкладів, якщо вивчається 9 дисциплін.

Розв'язання. Маємо розміщення з 9 елементів по 5 без пов­торень, їх кількість дорівнює

=98765=15120

Відповідь. 15120.

У розміщеннях без повторень не має однакових елементів у виборці: після вибору першого елемента для вибору другого еле­мента залишається на одиницю менше можливостей i т.д.

Означення. Розміщенням з повтореннями з n елементів по m елементів називається будь-який упорядкований m-елементний набір виду (а₁,а₂,…,а_m), де а₁,а₂,…,а_m - елементи множини М=(а₁,а₂,…,а_n), в якому хоч би один елемент повторювався.

Число всіх розміщень з повтореннями з n елементів по m елементів позначають символом 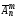. На відміну від розміщень без пов­торень, де mn, для розміщень з повтореннями може бути і m>n. Особливістю розміщень з повторенням е те, що після вибору першого елемента а₁ (М_i, записавши його на першому місці набору, його повертають у множину М, тобто число елементів множини М за­лишається сталим для вибору другого, третього і т.д. m-го еле­мента набору. Повторивши цю операцію m разів, дістаємо деяке розміщення з повтореннями з n елементів по m елементів. Тому розміщення з повтореннями з n елементів по m елементів ще нази­вають впорядкованими m-вибірками з n-елементної множини.

Теорема 2. Число розміщень з повтореннями з n елементів по m елементів обчислюють за формулою

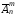= n^m , (3)

де m і n - натуральні числа.

Доведення. Перш за все відмітимо, що розміщення з повторен­нями з n елементів по m елементів можна одержати з розміщень по (m-1) елементу приєднанням ще одного елемента. Оскільки до кож­ного розміщення по (m-1) елементів можна приєднати будь-який з n елементів, то кожне розміщення по (m-1) елементу породжує n різ­них розміщень по m елементів, тобто

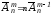. (4)

Тепер доведення формули (3) проведемо методом математичної ін­дукції по m.

1) При m=1 число розміщень дорівнює n:

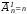
2) Припустимо, що формула (3) вірна для деякого m=k, тобто, що

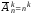
3) Доведемо, що при цьому формула (3) вірна також і для m=k+1,

тобто, що

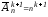
.Дійсно, користуючись формулою (4), знайдемо:

.

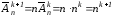4) Вимоги математичної індукції виконуються, тому формула (3) вірна для будь-якого натурального значення m.

Наслідок. Число підмножин n-елементної множини дорівнює 2ⁿ. Дійсно, нехай маємо множину М=(а₁,а₂,…,а_n), елементи якої пе­ренумеровані. Кожну підмножину множини М можна подати у вигляді упорядкованої n- елементної множини, елементами якої є нулі і одиниці, причому одиницю ставимо на тому місці, на якому знахо­диться певний елемент множини М, а нуль тоді, коли елемент мно­жини М не входить у підмножину. Наприклад, якщо М=(а₁,а₂,a₃,а₄), то набір (0;1;1;0) показує, що маємо підмножину (а₂,a₃), набір (0;0;0;0) - порожня множина, а набір (1;1;1;1) - це вся множина М.

Звідси випливає, що знайти число підмножин n-елементної множини М - це все одно, що знайти число перестановок з n елементів з повтореннями, 2-елементної множини (0;1). За формулою (1) число таких перестановок дорівнює 2ⁿ.

Приклад 2. До шестицифрових номерів телефонів входять цифри від О до 9. Скільки абонентів може обслуговувати телефонна станція?

Розв'язання. Оскільки цифри в номерах можуть повторюватись, то кількість шестицифрових номерів телефонів дорівнює числу роз­міщень з 10 елементів по 6 з повторенням, тобто

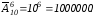
Відповідь. 1000000 абонентів.

Приклад 3. У селі проживає не менше 1000 жителів. Довести, що принаймні двоє з них мають однакові ініціали.

Розв’язання. В українському алфавіті 29 букв, які можуть бути ініціалами людини. Кількість всіх можливих різних пар ініціалів дорівнює числу розміщень з 29 букв з повтореннями, тобто

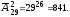
Відповідь. 841 різних пар ініціалів.