
- •Введение
- •12. Поверхностные интегралы.
- •12.2. Поверхностный интеграл 2-го рода.
- •13. Элементы теории поля
- •13.1. Некоторые понятия теории поля
- •13.2. Формула Грина.
- •13.3. Формула Остроградского-Гаусса.
- •13.4. Формула Стокса.
- •13.5. Оператор Гамильтона.
- •13.6. Специальные поля.
- •14.2.Основные действия над К.Ч.
- •14.5.Функции комплексного переменного.
- •14.8. Интегрирование ФКП.
- •14.9. Ряды с комплексными членами.
- •14.11.Вычеты и их применение.
- •15. Операционное исчисление.
- •15.3. Основные теоремы.
- •15.4. Обратное преобразование Лапласа.
- •16. Элементы математической физики
- •16.1. Основные понятия.
- •16.2. Классификация уравнений матфизики.
- •16.3. Вывод основных уравнений.
- •16.6. Метод характеристик.
- •16.6. Метод разделения переменных.
- •14.Теория функций комплексного переменного.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
Далее получаем при а – комплексном, |
равном α + β i |
: L( e(α +βi)t ) = |
||||||||||||||||||
1 |
|
= |
p −α |
|
+i |
|
ω |
|
|
|
|
. Теперь т.к. e(α +βi)t = |
|
|
||||||||
|
p − (α |
+ β |
i) |
( p −α) |
2 |
+ β |
2 |
( p −α) |
2 |
+ |
β |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
eαtt (Cosω t+iSinω t), |
|
то |
по равенству |
|
комплексных чисел получаем |
eαt Cosβ t |
||||||||||||||||
имеет |
изображением |
F(p)= |
p |
−α |
|
|
|
|
и аналогично |
eαt Sinβ t |
имеет |
|||||||||||
( p −α) |
2 |
+ β |
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
β
изображением F(p)= ( p −α)2 + β 2 .
15.3. Основные теоремы.
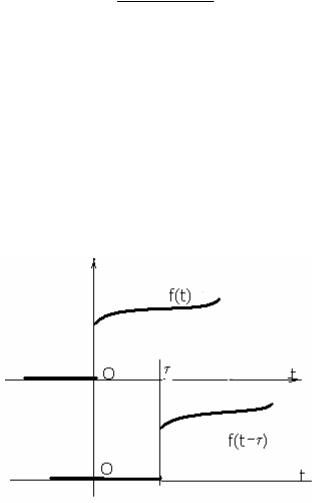
Теорема запаздывания. L(f(t-τ )) = e-p τ F(p) при τ >0.
Доказательство. L(f(t-τ )) = ∞∫e−pt f (t − τ )dt = |
τ∫e−pt f (t − τ )dt + |
0 |
0 |
+ ∞∫e−pt f (t −τ )dt .Первое слагаемое равно нулю (см. Рис 15.2). Во втором
τ
слагаемом сделаем замену t-τ =u , dt=du и пределы от t=0 до t =∞ и получим
∞∫e−pt f (t − τ )dt =0+ |
∞∫e−p(u+ τ ) f (u)du == |
∞∫e−p τ e−pu f (u)du == e−p τ |
∞∫e−pu f (u)du = e-p τ F(p). |
0 |
0 |
0 |
0 |
Рис 15.2. К теореме запаздывания.
Если же τ <0 , то получаем L(f(t+τ )) = ∞∫e−pt f (t + τ )dt и при замене t-τ =u ,
|
|
|
0 |
|
|
|
dt=du получаем пределы τ <u<∞ и интеграл ∞∫e−p(u− τ ) f (u)du = e p τ |
∞∫e−pu f (u)du = |
|||||
|
|
|
τ |
|
|
0 |
e p τ |
∞∫e−pu f (u)du = e p τ |
∞∫e−pu f (u)du − e p τ |
τ∫e−pu f (u)du = e-p τ |
(F(p) - e p τ |
τ∫e−pt f (t)dt ). Это |
|
|
τ |
0 |
0 |
|
0 |
|
фактически обобщает первый случай, т.к. при t<- |
τ имеем f(t)=0 и второе |
|||||
слагаемое в скобке выпадает. |
|
|
|
|
||
|
Комментарий. Следует быть внимательным при решении примеров. Если |
|||||
не оговорено “ …с применением теоремы запаздывания…“, то следует работать обычными приемами. Разберите решение Примера 15.3.
50
51
Помимо этого теорема запаздывания удобна при поиске изображений импульсных функций. См. решение примера 15.4.
Пример 15.3. Найдите изображение для f(t)=(t-2)2 непосредственно и пользуясь теоремой запаздывания.
Решение. L((t-2)2)=2!/p3+2/p2+1/p – использовано свойство линейности. L((t-2)2)=e-2p2!/p3 -если следовать теореме запаздывания. В первом случае использовано представление f(t) 1(t) =t2 1(t)+2t 1(t) +1(t), а во втором f(t-2)1(t-2) = (t-2)2 1(t-2), а потому и ответы разные.
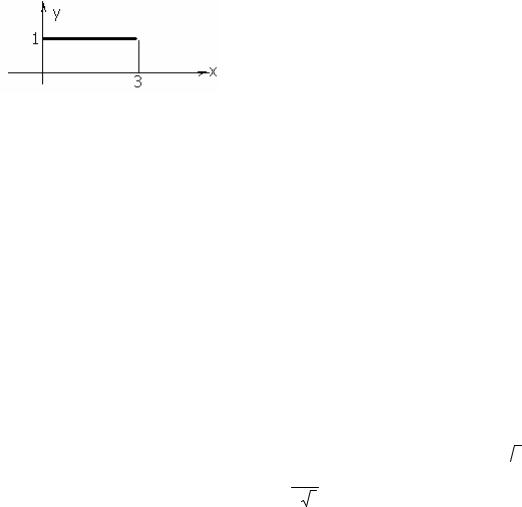
Пример 15.4. Найдите изображение для прямоугольного импульса высотой 1 и длиной 3.
Решение. Легко видеть, что импульс можно записать так 1(t)-1(t-3) (т.е. как разность единичной функции Хевисайда и ее же, сдвинутой на τ=3). Использовать линейность и теорему запаздывания и получить изображение для
1 |
-e |
-p 1 |
= |
1−e− p |
||
импульса F(p)= |
|
|
|
p . |
||
p |
|
p |
||||
Рис 15.3. К примеру 15.4.
Теорема о дифференцировании оригинала. Если f(t) непрерывна вместе со своей производной на [0; ∞) и если f `(t) – оригинал, то L(f `(t))=pF(p)-f(+0), где
f(+0) – правосторонний предел.
Доказательство. L(f `(t))= ∞∫e−pt f `(t)dt = ∞∫e−pt df (t) =e-ptf(t) |
|
∞ |
+p ∞∫e−pt f (t)dt = |
|
|
||||
0 |
0 |
|
0 |
0 |
|
||||
|
|
|||
=pF(p)-f(+0), т.к. интеграл во втором слагаемом уже известен, f(t) растет на бесконечности не быстрее экспоненты, а в нуле получаем по НьютонуЛейбницу f(0).
Следствие. Если f(t) непрерывна и дифференцируема вместе со своими производными на [0; ∞) и если f(n)(t) – оригинал, то L(f(n) (t))=p(n)F(p)-pn-1f(+0)-
pn-2f `(+0)-…-f(n-1) (+0). Доказательство по индукции. L(f `(t))=p(pF(p)-f(+0))- -f `(+0) и т.д.
Комментарий. Производные обязательно должны быть оригиналами! В противном случае могут быть неприятности . Например f(t)=  t - оригинал, но
t - оригинал, но
ее производная – уже не оригинал ( 21 t имеет разрыв 2-го рода в точке 0).
Это, пожалуй, самое ценное свойство прямого преобразования Лапласа, т.к. инженер-электрик сразу превращает задачу Коши для линейного Д.У. (наиболее распространенная задача ТОЭ) в обыкновенное линейное алгебраическое уравнение с неизвестным изображением решения. Подробнее об этом позже.
51
52
Эта теорема показывает ослабление устойчивости системы при введении в нее дифференцирующих звеньев.(См. следствие из теоремы существования и замедление стремления к нулю изображения производной. С точки зрения прикладника сравни поведение вагона с интегрированной (сплошной ) осью и поведение автомобиля на скользкой дороге, у которого колеса дифференцированы (вращаются независимо)).
И еще. В приложениях чаще всего f(0)=0. И поэтому комплексное число p при умножении выступает в пространстве изображений как оператор дифференцирования оригинала в пространстве оригиналов – еще одна интерпретация комплексного числа .
Теорема об интегрировании оригинала. Если f(t) |
оригинал с |
||
изображением F(p), то изображением |
∫t |
f (u)du является F(p)/p. |
|
|
0\ |
|
|
Доказательство. Из оценки |
подынтегральной функции |
ыв прямом |
|
преобразовании Лапласа следует, что ∫t f (u)du =ф(t) – тоже оригинал. Пусть его
0\
изображение равно Ф(p). Нам известно, что производная от интеграла с переменным верхним пределом равна подынтегральной функции в верхнем пределе. Тогда по теореме дифференцирования оригинала получаем
L(ф(t))=pФ(p)-ф(0). Но ф(0)= ∫0 f (u)du =0. И получаем pФ(p)= F(p). Откуда и
0\
следует верность теоремы.
Комментарий. По индукции из этой теоремы следуют изображения для целой степени tn . L(tn)=n!/p n+1 .
При введении в систему элементов интегрирования, система ‘усиливает’ устойчивость(См. предыдущий комментарий).
Правило затухания(смещение в изображении). Теорема. Если f(t)
оригинал с изображением F(p), то e-at f(t) имеет изображением F(p-a).
Доказательство. L(e-at |
f(t))= |
∞∫e−pt e−at f (t)dt = ∞∫e−( p−a)t f (t)dt = |
F(p-a). О чем |
||
предполагалось ранее. |
|
0 |
0 |
|
|
|
|
|
|
|
|
Дифференцирование |
изображения. |
Теорема. Если |
f(t) |
оригинал с |
|
изображением F(p), то –tf(t) имеет изображением F’(p). |
|
|
|||
Доказательство. F’(p)= (∞∫e−pt e−at f (t)dt)'p = ∞∫(e−( p−a)t f (t))'p dt = ∞∫e−pt (−t) f (t)dt , что |
|||||
|
0 |
|
0 |
0 |
|
является изображением –tf(t) по определению.
Изображение свертки функций. Определение. Сверткой функций f(t) и ф(t) называют выражение, обозначаемое f(t)*ф(t) и вычисляемое по правилу
∫t |
f (t − τ )ф(τ )d τ = ∫t |
f (τ )ф(t −τ )d τ . |
0 |
0 |
|
Как видим, свертка обладает некоим свойством симметрии.
Теорема. Изображением свертки оригиналов будет произведение свертываемых функций.
52
53
Доказательство. Отметим, что свертка оригиналов будет сама оригиналом, т.к. под интегралом окажется произведение ограниченных
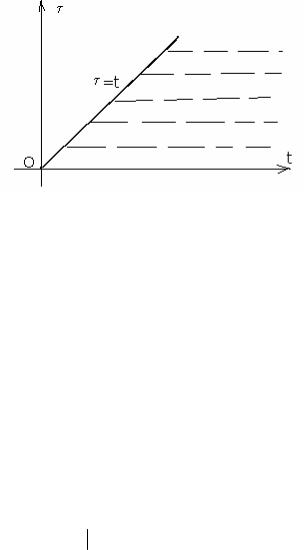
функций. Теперь предстоит вычислить L(f(t)*ф(t))= L( ∫t f (t − τ )ф(τ )d τ )=
|
|
|
0 |
∞ |
t |
|
Сменим порядок интегрирования в этих интегралах, |
∫e−pt ∫ f (τ )ф(t −τ )dτ dt . |
|||
0 |
0 |
|
|
руководствуясь Рис 15.4. Из рисунка видно, что интеграл по переменной τ распространен от 0 до прямой τ =t. А интеграл по переменной t - от нуля до бесконечности. При смене порядка для охвата заштрихованной области
потребуется изменение τ от 0 до бесконечности, а t - от τ до бесконечности. Предварительно занесем множитель e-pt под знак внутреннего интеграла, т.к. множитель не зависит от τ .
Рис 15.4. К теореме о свертке.
∞ ∞ |
|
∞ |
∞ |
|
В |
Получим новый интеграл ∫ ∫e−pt f (τ )ф(t −τ )dt dτ = ∫ f (τ ) ∫e−pt ф(t −τ )dt dτ . |
|||||
0 0 |
|
0 |
0 |
|
|
этом интеграле сделаем замену |
t-τ =u c пределами |
для u |
от 0 |
до |
|
∞ |
∞ |
|
∞ |
∞ |
|
= |
бесконечности. Получим ∫ f (τ ) ∫e−p(u+τ ) ф(u)du dτ = ∫ f (τ )e−pτ dτ ∫e−pu ф(u)du |
||||||
0 |
0 |
|
0 |
0 |
|
|
=F(p)Ф(p).
Из формулы для изображения свертки получают набор формул Дюамеля. Для этого следует взять производную от свертки по переменной t и результат приравнять к выражению для изображения производной
((f(t)*ф(t)))’=( ∫t |
f (t − τ )ф(τ )d τ )’t |
=pF(P)Ф(p)-( ∫t |
f (t − τ )ф(τ )d τ ) |
|
t=o = |
|
|||||
|
|||||
0 |
|
0 |
|
|
|
pF(P)Ф(p), т.к. последнее слагаемое равно нулю в точке t=0. Но слева производная от интеграла с параметром t по этому параметру равна
t
∫ ft' (t − τ )ф(τ )d τ ) t=o +f(0)ф(t). Получаем окончательно : изображением для
0
∫t |
ft' (t − τ )ф(τ )d τ ) |
|
t=o +f(0)ф(t) будет pF(P)Ф(p). |
|
|||
|
|||
0 |
|
|
|
Изображение импульсной функции. Пусть задана функция
|
|
при t < 0 и t < τ , |
f(t)= |
0 |
|
|
≠ 0 при t [0; τ ] |
53
