1

Математика для самообразования БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ

КАФЕДРА “ВЫСШАЯ МАТЕМАТИКА”

ЮДЕНКОВ Ю.Т.

Лекции по математике технического вуза

Сводный курс. Часть 3. Поверхностные интегралы. Теория поля. Теория функций комплексного переменного. Операционное исчисление.

Элементы математической физики.

Пособие разработано на основе лекций, читаемых на протяжении ряда лет студентам специальности АЭП (электропривод)

по дисциплине “ Высшая математика.”

2007 г.

Введение

Часть 3 курса лекций по математике технического ВУЗа является продолжением аналогичного курса лекций часть 1 и 2, которые включили в себя классические разделы математики : линейную и векторную алгебры, аналитическую геометрию, введение в математический анализ, дифференциальное исчисление функций одного и нескольких переменных, интегральное исчисление (определенный, неопределенный, несобственные, криволинейные и кратные интегралы), дифференциальные уравнения и теорию рядов.

12. Поверхностные интегралы.

Предполагается, что известны понятия одно- и двусторонних поверхностей и основных понятий теории поля. Используемые сокращения: ДИ – двойной интеграл, ПОВ-1

-изучаемый интеграл.

12.1.Поверхностный интеграл 1-го рода.

1

2

n

участке разбиения выберем точку Mk . Составим сумму ∑f (M k ) sk и вычислим

k =1

ее предел, когда размер частей разбиения стремится к ную, а их число к бесконечности.

Если существует указанный предел независимо от способа разбиения S на части и выбора точки Mk на каждой части, то такой предел назовем ПОВ-1 и

обозначим ∫∫f (M )ds .

S

Комментарий. Отметим внешнее сходство полученного интеграла с двойным. Отличие в том, что подынтегральная функция в ПОВ-1 зависит от трех переменных (является стационарным трехмерным скалярным полем). И еще – интегрирование в ДИ производится по плоской области, а в ПОВ-1 – по криволинейной поверхности S. Это становится заметным только в процессе вычисления.

Из способа получения ПОВ-1 следуют его основные свойства, полностью совпадающие со свойствами ДИ. Так же по типу совпадает и формулировка теоремы существования ПОВ-1.

Если S замкнутая , то ПОВ-1 записывают так ∫∫f (M )ds .

S

Для вычисления ПОВ-1 его следует свести к уже известному ДИ. Для этого используют рассуждения, которые применялись при вычислении площади поверхности с помощью ДИ. (см. раздел 13). Т.к. элемент ds равен

являются координатами нормали к поверхности, то заменяют ds одним из отношений. В подынтегральной функции из уравнения поверхности S находят переменную, которая не входит в элементы интегрирования. И тогда ПОВ-1

будет представлен для вычисления однои из двойных интегралов

∫∫f (M )ds = ∫∫f (x, y, z(x, y)) 1+ (zx' )2 + (z'y )2 dxdy =

Физически ПОВ-1 можно истолковать как массу неоднородной поверхности. Если же f(M)=1, то ПОВ численно дает площадь поверхности S.

Во всех случаях предполагается, что S однозначно проектируется на координатные плоскости. В противном случае следует разбить S на части, удовлетворяющие этим требованиям и воспользоваться свойствами интеграла.

12.2. Поверхностный интеграл 2-го рода.

Пусть задана двусторонняя поверхность S c границей Г. Пусть направление внешней нормали в любой точке М согласовано с движением по границе Г(правилом правого буравчика – если двигаться по внешней стороне поверхности вдоль границы, то точки , лежащие на внешней стороне, всегда располагаются слева от движения см.17.1.).

2

3

Пусть в каждой точке пространства, окружающего эту поверхность( и, следовательно, на самой поверхности) задано векторное поле

подынтегральная функция – скаляр, такой интеграл реален. С другой стороны,

→

величину пр→ F (M )ds можно истолковать как поток(количество, масса) поля n

→

F (x, y, z) , протекшего через площадку ds в направлении внешней нормали.

направлении внешней нормали к поверхности. Правую часть этого равенства называют поверхностный интеграл 2-го рода (далее везде ПОВ-2). В этой

→

записи имеется одна условность – вектор ds символический – его длина равна

→

ds, а направление совпадает с направлением нормали n к внешней стороне поверхности S. Если учесть , что координатами нормали являются

выражение под знаком ПОВ-2 не принято записывать в скобках, хотя интегрирование распространяется фактически на все слагаемые.

Для вычисления ПОВ-2 поступают так: записывают вместо одного выражения от трех слагаемых сумму трех разных интегралов

каждом из интегралов из уравнения S получают одну из трех переменных как функцию аргументов интегрирования ; последним действием учитывают взаимное расположение нормали к S и нормали к плоскости аргументов интегрирования и , при тупом угле между нормалями, перед интегралом меняют знак на противоположный.

Из схемы получения ПОВ-2 и его вычисления следует, что его свойства повторяют свойства определенного с одним отличием – при смене стороны

3

4

интегрирования весь интеграл меняет знак. Это не противоречит физическому понятию потока и согласовано с ним. Если интегрировать по одной стороне поверхности, то получаем отток среды через поверхность. Если же интегрировать по другой стороне, то происходит приток среды.

между ПОВ-1 специального вида и ПОВ-2.

13.Элементы теории поля

13.1.Некоторые понятия теории поля

Определение. Если в каждой точке М некоторого пространства задана величина U, то говорят, что в этом пространстве задано поле U.

Записывают этот факт так U=U(M). Фактически понятие поля – это физический термин для функции нескольких переменных.

Поведем простейшую классификацию полей : если U скаляр, то поле

→

называют скалярным; если поле векторное, то его обозначаютF (М).

Поля можно классифицировать по размерности: одномерные , если поле зависит от одной переменной; двумерные (плоские), если поле зависит от двух переменных; трехмерные (пространственные), если поле зависит от трех переменных.

Если среди аргументов функции имеется время, то поле называют нестационарным. Если зависимости от времени нет , то поле стационарное.

В теории поля часто работают с линиями и поверхностями. Во многих случаях их ориентируют. Ориентирование линии производят указанием направления движения на линии. Ориентирование поверхности выглядит несколько сложнее.

Поверхности могут быть односторонними или двусторонними.

Пусть имеется поверхность S с границей Г. Проведем нормаль к поверхности в некоторой точке М. Если теперь двигаться по выбранной внешней стороне поверхности вдоль границы Г, и точки поверхности остаются слева от движущегося, то говорят, что направление движения по границе согласовано (иначе поверхность правоориентирована).

Если в некоторой точке поверхности S провести нормаль к ней и затем двигать ее по внешней стороне , не пересекая границы и не отрывая от поверхности, и при этом нормаль в той же точке поверхности не принимает противоположного направления, то говорят, что поверхность двусторонняя.

Примером односторонней поверхности будет лист Мебиуса и бутылка Клейна.

13.2. Формула Грина.

Существует обобщенная связь между КРИ-2 по замкнутому контуру и ДИ по области, которая ограничена эти контуром. Эту связь устанавливает формула Грина.

4

5

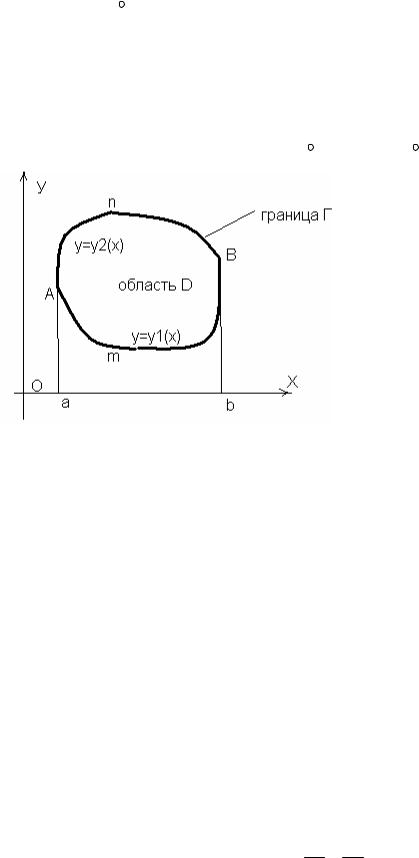
Теорема. Если функции P(x;y) и Q(x;y) непрерывны вместе со своими частными производными в односвязной области D с границей L , то

Рис 13.1. К выводу формулы Грина.

Аналогичное доказательство можно сделать для второго слагаемого под знаком ДИ.

Из доказательства следует условие независимости КРИ-2 от пути интегрирования. Поясним термин “независимость от пути интегрирования”.

P(x; y)dx +Q(x; y)dy

Пусть нам задан некоторый КРИ-2 ∫P(x; y)dx +Q(x; y)dy . Пусть путь L –

L

это кривая AmB на Рис 17.1. Пусть мы вычислили этот же интеграл , но по пути AnB. Если при этом окажется , что результаты равны, независимо от выбора

линии, соединяющей тоски А и В, то говорят, что ∫P(x; y)dx +Q(x; y)dy не

L

зависит от пути интегрирования. Это же утверждение эквивалентно утверждению ∫ P(x;y)dx+Q(x;y)dy=0. В самом деле, один участок общего

AmBnA

контура мы пройдем в положительном направлении, а второй – в отрицательном. В сумме будет нуль, т.к. исходные равны (не зависели от пути).

Во многих случаях доказать второе легче первого.

Теорема. Для того, чтобы ∫P(x; y)dx +Q(x; y)dy не зависел от пути

L

интегрирования необходимо и достаточно, чтобы ддPy = ддOx .

5