
- •Введение
- •12. Поверхностные интегралы.
- •12.2. Поверхностный интеграл 2-го рода.
- •13. Элементы теории поля
- •13.1. Некоторые понятия теории поля
- •13.2. Формула Грина.
- •13.3. Формула Остроградского-Гаусса.
- •13.4. Формула Стокса.
- •13.5. Оператор Гамильтона.
- •13.6. Специальные поля.
- •14.2.Основные действия над К.Ч.
- •14.5.Функции комплексного переменного.
- •14.8. Интегрирование ФКП.
- •14.9. Ряды с комплексными членами.
- •14.11.Вычеты и их применение.
- •15. Операционное исчисление.
- •15.3. Основные теоремы.
- •15.4. Обратное преобразование Лапласа.
- •16. Элементы математической физики
- •16.1. Основные понятия.
- •16.2. Классификация уравнений матфизики.
- •16.3. Вывод основных уравнений.
- •16.6. Метод характеристик.
- •16.6. Метод разделения переменных.
- •14.Теория функций комплексного переменного.

14
системой координат z M(x, y) . C другой стороны z можно поставить в соответствие радиус-вектор на той же плоскости, проведенный из начала координат в точку z. Если при этом учесть, что в математике принято рассматривать свободные векторы, то возможности интерпретации существенно расширятся. Этим представляется возможность удобного манипулирования разными понятиями в разных ситуациях. С другой стороны, усложняется возможность начального усвоения некоторых соотношений, изучаемых по разным литературным источникам, т.к. часто неизвестно, на какую именно интерпретацию опирается при рассуждениях автор данной книги. По возможности (там, где это не является само собой разумеющимися) будем эти моменты отражать.
Исходя из указанных соображений, получаем две формы записи для
комплексного числа z=x+iy=rCosф +rSinф=r(cosф+iSinф), где |
|
(1) |
|
r=¦z¦= x2 + y2 = Re2 |
z + Im2 z - модуль z, ф=arctg(y/x)=argz |
- |
аргумент |
комплексного числа - |
два новых понятия. При этом договоримся: |
r |
- всегда |
положительная величина (расстояние от начала координат до точки z), определяемая однозначно; ф - угол между положительным направлением оси Ох и направлением на точку z, отсчитанный против часовой стрелки. (здесь следует быть внимательным, т.к. разные авторы предполагают различные направления отсчета и поэтому рабочие формулы могут отличаться). Это значит, аргумент определяется с “точностью” до слагаемого 2kπ. При этом дополнительное слагаемое может появиться в совершенно неожиданных местах, “удобных” для работы в данной ситуации.
Если использовать формулы Эйлера: 0,5(eiy+e-iy ) = Cosy и 0,5(eiy-e-iy
)/i=Siny,то получим |
|
z=x+iy=rCosф +rSinф=r(cosф+iSinф)=re iф |
(2) |
Комментарий. В (2) могут использоваться различные из форм записей для действительной и мнимой частей, модуля и аргумента комплексного числа.
14.2.Основные действия над К.Ч.
Определим основные действия над комплексными числами.
Равенство. z1=z2 |
<==> x1 = x2 , |
(3) |
|
y1 = y2. |
|
Как видно, это - самое простое определение. Можно, конечно,
договориться (так оно и подразумевается по умолчанию - default) считать
равными комплексные числа, если их модули равны, а аргументы отличаются
на 2kπ. Это будет несколько сложнее, т.к. гораздо проще рассматривать две
совпадающие точки плоскости.
Сопряжение. z* сопряжено z, если |
Re z* = Re z, |
(3a) |
|
||
|
Im z* = Im z. |
|
14

15
Суммирование. z=z1+z2 |
x = x1 |
+ x2 |
, |
(4) |
<==> |
+ y2. |
|||
|
y = y1 |
|
||
Легко истолковать действие суммирования . Это одно из : - построение суммы двух векторов;
- сдвиг точки z1 на вектор z2 (или сдвиг точки z1 на вектор z2);
- комплексное число в операции сложения выступает как оператор параллельного переноса. Использовать это в зависимости от ситуации.
Умножение. z=z1*z2 <==> |
|
|
z |
|
= |
|
z1 |
|
|
|
z2 |
|
, |
(5) |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
+arg z2. |
||||
|
arg z = arg z1 |
|
||||||||||||
Как видим, умножение проще определять, если рассматривать экспоненциальную форму числа z.
z = z1z2 = r1r2 ei(φ1 +φ2 ) .
Легко истолковать действие умножения:
- деформация вектора z1 на величину | z2| с одновременным поворотом полученного на угол argz2 против часовой стрелки; комплексное число в операции умножения выступает как оператор деформации и поворота.
Возведение в натуральную степень. Определим, используя экспоненциальную форму и обобщение умножения. Получаем
zn = |
|
z |
|
n ei(arg z+2kπ) =r (Cos(nф) +iSin(nф)). |
(6) |
|
|
|
|
|
|
|
|
|
|||||
|
|
Если возводят в отрицательную целую степень, то это выполняют в |
|||||||
последовательности: сначала используют запись |
z−n = |
1 |
, |
затем в |
|||||
zn |
|||||||||
|
|
|
|
|
|
|
|
||
знаменателе используют возведение в натуральную степень и потом действие деления как обратное относительно умножения. Получают
z−n = |
|
z |
|
−n ei(− arg z+2kπ) =r (Cos(-nф) +iSin(-nф)). |
(6а) |
|
|
||||
Извлечение корня из комплексного числа |
|
||||
Используем определение : корнем степени |
n из комплексного |
||||
числа z назовем такое комплексное w, для которого wn=z. |
|
||||
Из определения следует : |w|n =|z| и argz+ 2kπ=n argw. Отметим, что слагаемое 2kπ можно расположить с любой стороны от знака равенства. Но в
данной |
ситуации удобно |
это сделать слева, |
т.к. корень |
|
извлекают |
из |
|||||||||
“известного” |
|
|
числа |
z. |
Из |
полученных |
соотношений следует |
: |
|||||||
n z = w = n |
z |
и |
arg n |
z = arg w = arg z + 2kπ , а потому получаем формулу |
|||||||||||
|
|
|
|
|
arg z+2kπ |
|
n |
|
|
|
|
|
|
||
|
n |
|
|
z ei |
|
|
|
|
|
|
|
|
|||
Муавра |
z = n |
|
|
. |
Для |
которой можно |
принять |
геометрическое |
|||||||
|
n |
||||||||||||||
истолкование |
: |
корень степени n из z - это n вершин правильного |
|||||||||||||
многоугольника, вписанного в окружность радиуса |
n z с центром в начале |
||||||||||||||
координат. При этом одна из вершин находится на направлении |
|
arg z |
. |
|
|||||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
15

16
14.3.Понятие о расширенной комплексной плоскости.
Рис 14.1.Сфера Римана на комплексной плоскости.
Пусть на плоскости с введенной системой декартовых координат расположена сфера радиуса 1 так, что точкой касания сферы и плоскости является точка S(южный полюс) - начало координат. Точка на сфере, расположенная на диаметре, который проходит через S , будет N (северный полюс). Возьмем на плоскости произвольную z. Соединим ее с N . В таком случае мы получим соответствие точек плоскости и точек сферы. Сферу называют сферой Римана, а соответствие - проекциями Меркатора. Отметим, что взаимно-однозначного соответствия не будет, если не договориться о точке N. Тогда рассуждаем так: если удалять z по плоскости от точки S в любом направлении и по любому пути, то соответствующая ей точка на сфере будет приближаться к северному полюсу N.
Введем понятие ∞-удаленной точки так - это точка, которой на сфере Римана соответствует северный полюс S. При таком соглашении между точками сферы Римана и точками комплексной плоскости (плоскости хОу) устанавливается взаимно-однозначное соответствие. Это значит, что любой точке на плоскости с введенной ∞-удаленной точкой на сфере Римана соответствует единственная точка и наоборот. Комплексную плоскость с введенной ∞-удаленной точкой называют расширенной комплексной плоскостью.
Отметим интересные факты , вытекающие из такого соответствия. Вопервых, обнаруживается, что это совсем не противоречит реалиям, т.к. находясь на южном полюсе, мы всегда смотрим на север. Т.е. |0|=0 и arg0 - любое. Это соответствует понятию нулевого вектора. Если же находиться на северном полюсе (в ∞-удаленной точке), то мы всегда смотрим на юг. А это означает, что
| ∞-удаленной точки |= ∞, а arg( ∞-удаленной точки) - любой. Интересно, что образом прямой на плоскости при таком соответствии
является окружность, которая проходит через северный полюс. Прямым пересекающимся в данной точке плоскости, соответствует две окружности, которые пересекаются в двух точках, одна из которых ∞-удаленная точка.
16

17
Параллельным прямым соответствуют две окружности , касающиеся в ∞-удаленной точке.
Т.о. в дальнейшем не будем делать принципиального различия между прямыми и окружностями, т.к. предполагаем во многих случаях, что расширенная плоскость представляет собой сферу, что часто более удобно(по крайней мере, если приходится рассматривать поведение некоторых объектов достаточно далеко от нашего местоположения).
14.4. Понятие области, границы, окрестности.
Пусть Е - некоторое множество в расширенной комплексной плоскости. Определение. Точку z называют внутренней для Е, если существует
достаточно малый круг, все точки которого принадлежат Е.
Определение. ε - окрестность точки zo - это ε - окрестность точки zo окружности с центром в zo и радиусом ε.
Определение. ε - окрестность ∞-удаленной точки - это внешность круга достаточного большого радиуса и центром в начале координат.
Определение. zo - граничная для Е, если в любой ε - окрестности точки zo имеются как точки из Е, так и точки , не принадлежащие Е.
Определение . zo - внешняя для Е, если существует ε - окрестность точки zo , в которой нет точек , принадлежащие Е.
Определение. Область D - это множество точек комплексной плоскости С, таких что:
-состоит только из внутренних точек D;
-любые две точки D можно соединить между собой непрерывной линией, целиком состоящей из точек D.
Определение. Область D ограничена, если она целиком располагается в окружности конечного радиуса и центром в начале координат.
Определение. Область D замкнута, если кроме внутренних точек ей принадлежат и граничные.
Границей может быть линия, разрез, точка.
Определение. Число частей границы, не имеющих общих точек - порядок связности области.
Рис 14.2. Области и границы (слева – односвязная область; справа – ограниченная замкнутая, двусвязная область с разрезом)
14.5.Функции комплексного переменного.
Определение. Если любому z по закону f(z) ставится в соответствие одно или несколько комплексных w, то говорят, что задана ФКП.
17

18
Обозначают это w=f(z). Но, ввиду возможности записать всякое комплексное в различных видах, имеется целый “букет” для записи ФКП.
w=f(z)=u+iv=f(x+iy)=u(x;y)+iv(x;y)=u(r,ф) +iv(r;ф)=|w|eiragw =u(|w|;argw) + iv(|w|;argw) и т.д. Они используются по необходимости. В этом трудность изучения теории ФКП. Иногда вместо w задают запись в виде системы
u =u(x; y),v = v(x; y).
Пример 14.1. Записать некоторые возможные выражения для w=z2 .
Решение. |
Задана |
|
функция, т.к. w=u+iv=(x+iy)2 |
= (x2-y2)+i(2xy). Отсюда |
|||||||||||||||||||
|
|
|
|
= |
x |
2 |
− |
y |
2 |
; Или иначе |
|
= |
Re w |
= |
x |
2 − |
y |
2 |
; |
u = |
w Cos arg w; |
или |
|
получаем u |
|
|
|
|
u |
|
|
|
|
или |
( ( |
|
|||||||||||
|
|
|
|
v = 2xy. |
|
|
|
v = Im w = 2xy. |
|
|
v = |
(w(Cos arg w. |
|
||||||||||
|
2 |
Cos2arg z; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
u = r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
v = r2Cos2arg z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Комментарий. |
|
Фактически |
w=f(z) |
- |
это |
известное нам |
отображение |
|||||||||||||||
одного множества на другое. В данном случае одной комплексной плоскости на другую комплексную плоскость. Чаще всего образ и прообраз изображают на одной и той же комплексной плоскости.
Определение. Пусть w=f(z) определена в окрестности точки zo . Ее
называют непрерывной в zo, если |
lim w = 0 |
. Или иначе f (z) → f (zo ) ≠ ∞. |
|
z → 0 |
|
Теорема. Для того , чтобы f(z) была непрерывна в zo необходимо и достаточно, чтобы в этой точке были непрерывны ее действительная и мнимая
части. |
|
|
|
|
|
Доказательство. |
Оно |
следует |
из |
очевидной |
записи |
w(z) = u(x; y) + iv(x; y) . |
|
|
|
|
|
Необходимость. Пусть w непрерывна в z=(х;у). Тогда существует предел слева, равный нулю. Но тогда существуют пределы выражений , записанных справа и, ввиду равенства комплексных чисел, эти пределы равны нулю. Следовательно, u и v непрерывны в той же точке.
Достаточность. Пусть u и v непрерывны в z=(х;у). Тогда существуют пределы выражений , записанных справа и они равны нулю. Поэтому существует предел слева, равный нулю. И значит w непрерывна в той же точке.
Элементарными ФКП будем называть функции :
-линейную - f(z)=az+b, где a,b некоторые комплексные константы;
-экспоненту - f(z)=ez;
-дробнолинейную функцию f(z)= czaz ++ db , ac ≠ bd;
-комплексный логарифм f(z)=Lnz;
-степенную функцию f(z)=zn=|z|nenz
-комплексные гармоники f(z)=Sinz=(eiz-e-iz)/(2i)=-0,5i(eiz-e-iz);
f(z)=cosz=(eiz+e-iz)/2=0,5(eiz+e-iz);
и др.
18

19
Следствия.
Все элементарные функции непрерывны в своей области определения. Сумма , разность, произведение, частное непрерывных функций
непрерывны.
Пример 14.2. Решите уравнение Cosz=3.
Решение. Имеем eiz+e-iz=6. Откуда получаем ei2z-6eiz+1=0. Сделаем замену еiz=t. И получим решение квадратного уравнения. Далее получаем еiz= 3 ± 2 2
2
Откуда |
iz=Ln( 3 ± 2 2 ) |
. |
Далее |
z=-iLn( 3 ± 2 |
2 ) |
= |
- |
i(ln| 3 ± 2 2 |+iarg( 3 ± 2 2 ))= 2kπ +iln| 3 ± 2 2 | и |
получаем две |
серии |
точек |
||||
плоскости z расположенных на двух |
горизонталях у=ln( 3 ± 2 2 ) |
через |
|||||
промежутки 2π вдоль оси Ох.. |
|
|
|
|
|
|
|
14.6. Производная ФКП и аналитические функции.
|
Определение. |
Если |
существует |
конечный |
предел |
||
lim |
f (z + z) − f (z) |
,независимый от того, как z |
стремится к нулю, |
то этот |
|||
z |
|||||||
|
|||||||
z → 0
предел называют производной от ФКП и обозначают w’=f’(z).
Теорема существования. Для того, чтобы w=f(z) имела производную, необходимо и достаточно, чтобы были непрерывны и дифференцируемы по обоим аргументам ее действительная и мнимая части и были выполнены
|
∂u |
= ∂v |
|
|||
условия |
|
∂x |
∂y |
. |
||
|
||||||
|
|
∂u |
= − |
∂v |
|
|
|
|
∂y |
|
|
∂x |
|
|
|
|
|
|
||
Комментарий. Эти условия были получены сразу несколькими математиками и потому их часто называют условиями Коши-Римана-Эйлера- Д’Аламбера . Мы их будем записывать аббревиатурой КРЭДА.
Доказательство. (Мышкис А.Д.) Имеем по определению
w’= |
dw |
= = |
du +idv |
= |
u 'x dx +u 'y dy +i(v'x dx +v'y |
dy) |
. |
dz |
dx +idy |
dx +idy |
|
||||
|
|
|
|
|
Чтобы полученное было верно при любом пути стремления z к zo потребуем сначала чтобы dy=0 и dx-->0. Тогда получаем w’=u’x+iv’x . Если же потребовать, чтобы dх=0 и dу-->0, тогда получим w’= v’y -iu’у . Для получения единственного результата из равенства комплексных чисел получаем условие КРЭДА.
Пример 14.3. Вычислите, если возможно, производную функции f(z)=az+b .
Решение. Вычислим сначала Re(az+b) и Im(az+b). Для этого преобразуем саму функцию (a1+ia2)(x+iy)+b1+ib2=a1x-a2y+b1+i(a2x+a1y+b2). Откуда получаем
19
|
|
|
|
|
|
20 |
u = a x −a y +b , |
Теперь проверим выполнения условий КРЭДА. |
|||||
|
1 |
|
2 |
1 |
||
v |
= a2 x + a1 y +b2. |
|
||||
|
u ' |
|
= a = v' |
, |
для любой точки комплексной плоскости. |
|
Имеем : |
|
x |
1 |
y |
|
|
u 'y = −a2 = −v'x . |
|
|||||
Условия |
КРЭДА выполнены. Производная существует и может быть |
|||||
вычислена по одной из ранее приведенных формул. Она равна w’= u’x +i v’x = a1
+i a2 =a или v’y -i u’y = a1 +i a2 =a.
Следствие. Производную можно находить по любой из формул, полученных на основании КРЭДА : w’= u’x +i v’x = v’y +i v’x = u’x -i u’y =
=v’y -i u’y = и т.д.
Определение. Функцию, имеющую производную в данной точке, называют дифференцируемой в этой точке.
Определение. Функцию, имеющую производную в области, называют аналитической в области.
Сравнив два определения, мы видим их существенную разницу. Поясним это с утилитарной позиции - функция будет аналитической в точке, если она имеет производную в точке и в некоторой окрестности этой точки. Последнего не требуется для дифференцируемой функции.
Пример 14.4. Вычислите, если возможно, производную функции
f(z)=zRez |
|
|
|
Решение. Вычислим сначала Re(zRez)= |
и Im(zRez). |
Для |
этого |
преобразуем саму функцию (x+iy)x=x2+ixy. Откуда получаем u= |
x2, |
v=xy |
|
Теперь проверяем условия КРЭДА u’x=2х; v’y=х; u’y=0; v’x=y. Условия КРЭДА выполняются только в одной точке (0;0). Производная в этой точке равна 0. В других точках производной нет. И потому функция дифференцируема в этой точке, но нигде не аналитична.
Определение. Точки, в которых ФКП аналитична , называют правильными (точками регулярности).
Комментарий. Учебники по ТФКП могут носить в заголовках термин “...аналитических функций... или “...функций комплексного переменного...”. Следует относиться к этому спокойно. Как было видно ФКП обобщают функции со специальными свойствами - аналитические. Для начинающего и специалиста-прикладника следует просто это учитывать.
Отметим основные свойства аналитических функций.
Теорема. Производная аналитической функции будет функцией аналитической.
Доказательство. Пусть w’= u’x +i v’x = v’y +i v’x = u’x -i u’y . Для аналитичности вновь полученной функции требуется , чтобы u’’xx=(u’x)’x= =(v’y)’x =v’y’x. Но это (v’х)’у=v’x’y .А смешанные производные равны . Аналогично для второго соотношения из КРЭДА.
Для аналитических функций справедливы известные теоремы о производных: (f+ф)’=f’+ф’; (cf)’=cf’; (fф)’=f’ф+fф’; и т.д. для дроби, для сложной функции и обратной.
20

21
Можно построить простой алгоритм вычисления производной ФКП:
-проанализировать ФКП на предмет элементарности; если она элементарна, то вычислить производную по известным правилам; если f(z) трудно отнести к элементарным, то перейти к следующему пункту;
-выделить Re(f(z)) и Im(f(z));
-вычислить частные производные , необходимые для проверки КРЭДА;
-проверить, где выполняются и выполняются ли условия КРЭДА;
-там, кде условия КРЭДА выполняются вычислить производную по одной из удобных формул.
С понятием аналитической функции связано понятие гармонической функции.
Определение. Функция, имеющая в D непрерывные частные до второго
порядка включительно и удовлетворяющая уравнению Лапласа ∂2 u + ∂2 u = 0,
∂x2 ∂y2
называется гармонической.
Комментарий. Не следует путать понятие гармонической функции и гармоники.
Пример 14.5. Функция exCosy - является гармонической, что легко проверить.
Теорема. Если w=f(z)=u+iv аналитична, то u(x;y) и v(x;y) - гармонические функции.
Доказательство. Т.к. w аналитична, то справедливы соотношения
∂u |
= ∂v |
|
∂ |
|
|
(∂u) = |
∂ |
(∂v ) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∂x |
∂y |
.Поэтому |
|
∂x |
∂x |
|
∂x ∂y |
. Если подставить значения |
|||||||||||
|
|
|
|
||||||||||||||||
|
∂u |
= − |
∂v |
|
|
∂ |
( |
∂u |
) = |
∂ |
(− |
∂v |
) |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∂y |
∂x |
|
|
∂y |
∂y |
∂y |
∂x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
левых частей последних равенств в уравнение Лапласа, то и получим требуемое. Аналогичное верно для v(x;y).
Определение. Две гармонические функции, связанные по КРЭДА называют сопряженными гармоническими.
Комментарий. Не всякие две гармонические сопряженные формируют аналитическую.
Примером сопряженных гармонических являются поле потенциалов и поле эквипотенциалей.
Теорема. Для сопряженных гармонических u и v справедливы соотношения: ∫udx − vdy =∫vdx + udy =0 .
c |
c |
Доказательство. По формуле Грина для КРИ-2 проверим условие равенства нулю каждого интеграла. Проверка приводит к соотношениям КРЭДА, которые верны для u и v.
Пример 14.6. Восстановите действительную часть аналитической функции, если известна сопряженная ей мнимая часть v=x2-y2+xy.
21
22
Решение. Находим v’y=-2y+x . Но это равно u’x . А потому u= ∫(2y + x)dx + C(y) =2xy+0,5x2+C(y). Но u’y=-v’x. Получаем 2x+C’y(y)=-2x+y.
Из этого равенства получаем C’y(y)=-y. Откуда C(y)=-y2 . Получаем окончательно сначала действительную часть u=2xy+0,5x2-y2 . А затем и
w=2xy+0,5x2-y2+i(x2-y2+xy).
Аналитические функции тесно связаны с векторными полями. Согласно
→ |
→ |
определению потенциального поля a оно обладает свойством rot a =0. Возьмем произвольную u(x;y) и вычислим gradU= U и это поле потенциальное. Причем U - его потенциал. При этом rot(gradU)= U=0=u’’xx+u’’yy , т.е. соответствует определению гармонической функции. Иначе говоря, гармоническую функцию можно истолковать как потенциал плоского поля. При этом линии u(x;y)=C можно рассматривать как эквипотенциали, а линии v(x;y)=C , где v сопряженная для u - как как силовые линии, т.к. они ортогональны в точках пересечения. В самом деле, grad U=u’xi+U’yj - перпендикулярен U=C; а grad V=V’xi+V’yj перпендикулярен V=C. Следовательно, градиенты перпендикулярны, если учесть условия КРЭДА.
Обобщаем: аналитическая W=u+iv - это комплексный потенциал (силовое поле) с силовыми линиями u=C и эквипотенциалями v=C.
Установим еще геометрический смысл модуля и аргумента производной
аналитической |
функции. |
Сначала |
|f(z)| = lim |
|
|
f |
|
|
= lim |
|
|
w |
|
. |
Отсюда |
|||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
z |
|
|
|
|
z |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z → 0 |
|
|
|
|
|
|
||||||
следует, что |
|
|
w |
|
=|f(z)| |
|
|
z |
|
. Т.е. модуль производной аналитической функции |
||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
- это коэффициент деформации комплексной плоскости в |
точке |
z при |
||||||||||||||||||||||||
отображении w=f(z). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Теперь для аргумента производной получаем arg w=argf ‘z)= |
|
|||||||||||||||||||||||||
=arglim |
f =arg |
|
w -arg |
|
|
z. Это |
значит, |
что |
|
аргумент |
производной |
|||||||||||||||
z→0 |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
аналитической функции указывает величину угла поворота комплексной плоскости в точке z при отображении w=f(z).
Определение. Отображение комплексной плоскости, сохраняющее величину угла поворота и величину коэффициента деформации кривых, проходящих через данную точку, называют конформным.
14.7. Задачи на конформные отображения и отображения элементарными функциями.
Этот раздел можно без потерь пропустить тем, кто не соприкасается с операциями в гидрогазоили электродинамики, или не связан с вопросами расчета полей.
Мы знаем, что для аналитической в области ФКП w=f(z) имеет место : argf’(z) – указывает на величину угла поворота комплексной плоскости в
данной точке при отображении w=f(z); величина этого угла поворота
22

23
сохраняется для ВСЕХ кривых (линий), проходящих через ДАННУЮ точку (деформация «в малом» - свойство консервативности углов);
| w’| - указывает на величину деформации (растяжение или сжатие в «малом» ) комплексной плоскости в данной точке; естественно, что все кривые, проходящих через ДАННУЮ точку, деформируются одинаково.
Определение. Отображение расширенной комплексной плоскости @z называется конформным в точке z, если бесконечно малые дуги ВСЕХ кривых, проходящих через эту точку, деформируются и поворачиваются одинаково.
Т.о. отображение, осуществляемо аналитической функцией комплексного переменного – конформное отображение.
Свойства таких отображени используют в практичеких приложениях теории аналитических ФКП.
На практике встречаются два вида задач.
1-я задача: Найти (получить, вывести) такую w=f(z), которая однолистно (однозначно) и конформно отображает область D в область G.
Эта задача не всегда имеет решение, т.к., например, многосвязную область не отобразишь в односвязную.
2-я задача: Найти (изобразить, построить) такую G, в которую данная w=f(z) отображает заданную D.
При решении этих задач использую некоторые теоремы о ФКП. Теорема существования. Если D и G произвольные, односвязные,
отличные от @z и от расширенной @z с одной (любой) выколотой точкой, то существует однолистное и коформное отображание w=f(z) такое, что D переходит (превращается ) в G.
Отметим, что теорема указывает только на существование, а, следовательно, возможностей отобоазить может быть достаточно много. И всегда имеется возможность выбрать более удобное или более простое с практической точки зрения отображение.
Для выбора такого единственного отображение применяют так называемое нормирование для w=f(z). Суть нормирования заключается в задании некоторых дополнительных условий, накладываемых на искомое отображение. Примеры таких условий : задают образы одной внутренней и одной граничной точки области D; задают образы трех упорядоченных точек границы D (упорядоченность – указание, какая из точек следует за какой); задают в zo D значение wo=f(zo) и argf’(zo)=фо и т.д.
Из этих замечаний следует, что для “хорошего” отображения D в G достаточно научиться отображать каждую из них на нечто стандартное, а затем произвести суперпозицию (наложение) отображений и получить требуемое отображение.
Теорема о принципе соответствия границ. Пусть односвязные D и G
ограничены соответственно линиями (контурами) l и L. Причем положительные
обходы согласованы. Пусть f(z) аналитическая вD =D+ l (замкнутой, т.е. включающей границу l области) отображает l на L. Тогда f(z) – есть однолистное и конформное для отображени D на G.
23
24
Из этой теоремы следует: найди f(z) , которая отображает l на L; установи направление обхода области D и тогда сразу обнаружишь расположение G “внутри” ее границы L.
При решении нижеприведенных задач будем руководствоваться этими теоремами и опрделением конформного отображения. Использовать теоремы будем по мере необходимотси для облегчения работы.
Сначала рассмотрим стандартные конформные отображения. Именно на них строятся более сложные отображения. Отработаем приемы необходимых элементарных преобразований и выясним их геометрический смысл. Затем будем работать готовыми блоками преобразований и отображений. Будем получать качественное отображение (в котором содержится существо вопроса), а уточнять детали будем количественно (расположение конкретных точек, уравнения линий и т.д.).
Чтобы было понятно, для чего выполнены те или иные преобразования вспомним некоторые сведения из аналитической геометрии (геометрии в формулах).
Так, например, известно, что любая кривая на плоскости с декартовыми координатами хОу (т.е. комплексной плоскоти z) – это уравнение с двумя переменными F(x;y)=0. При отображении (любом) w=f(z) мы переходим из одной плоскости комплексного переменного z в другую плоскость комплексного переменного w с декартовыми координатами uОv. Поэтому для получения образа Ф(u;v)=0 кривой F(x;y)=0 в новой системе координат следует из уравнения F(x;y)=0 исключить переменные х и у и получить уравнение, содержащее только переменные u и v. В этом случае говорят о количественных преобразваниях.
Вдругих случаях, при необходимости, будем использовать
преобразования качественные, когда выполняем действия, опираясь на принципиальные свойства или характеристики, без указания цифровых или буквенных характеристик.
Естественно при решении задач будем делать об этом предупреждения. Пример 1. Известна элементарная функция w=az+b, a,b – коплексные
постоянные. Вясним, что происходит с комплексной плоскостью при таком отображении.
Качественный подход. Данная функция – аналитическая на всей @z. Производная w’=a – константа. Это значит, что при таком отображении плоскость @z равномерно деформируется с коэффициентом k=| w’|=| a | (т.е. равномерно растягивается от начала координат при | a |>1 или равномерно координат при | a |<1). После этого вся плоскость вектора b. (Смотри геометрический смысл комплексных чисел – сложение векторов по правилу
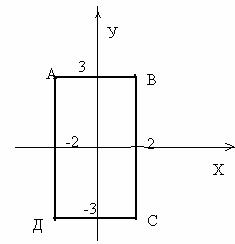
. Пусть нам задан прямоугольник уравнениями уравнение w=az+b в виде
24
25
w= (a1 +ia2 ) (x+iy)+ (b1 +ib2 ) . Из этого соотношения следует, что
u = a1x −a2 y +b1, (*)v = a2 x + a1 y +b2.
Выясним, как выглядит конкретно уравнение отрезка , например, ВС при таком отображении. Для этого подставим в формулу (*) значение х=2 – т.е.
уравнение стороны ВС на плоскости z. |
Получаем |
u = 2a1 −a2 y +b1, |
|
|
+ a1 y +b2. |
||
|
|
v = 2a2 |
|
Рассматривая переменную у в этой системе как параметр, легко сделать вывод, что мы получили параметрическое уравнение прямой линии – образа отрезка ВС, но уж`е на комплексной плоскости w (т.е. в декартовой системе uOv). Если это затруднительно для понимания, то можно из этих равенств исключить переменную у и получить явное уравнение прямой в декартовой системе uOv. В
самом деле, из |
1-го |
уравнения |
имеем |
у= 2a1 +b1 −u . Если |
полученное у |
|||||
|
|
|
|
|
a2 |
|
|
|
|
|
подставим во 2-е уравнение, то останется записать |
|
|
|
|
||||||
v=2a2+b2+a1 |
2a1 +b1 −u . Или v=- |
a1 |
u+(2a2+b2+ |
a1 |
2a1 +b1 |
) – типичное |
||||
a |
||||||||||
|
a |
2 |
|
|
|
|
a |
|
||
|
|
2 |
|
a1 |
|
2 |
|
|||
уравнение прямой с |
угловым |
коэффициентом - |
. |
Эту |
прямую при |
|||||
|
||||||||||
|
|
|
|
|
|
a |
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
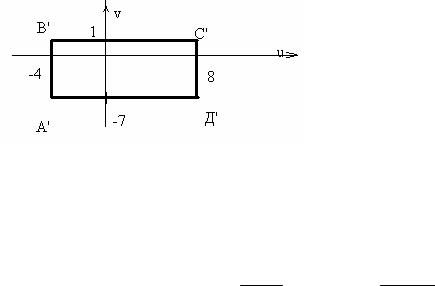
необходимости легко нарисовать и получить образ ВС при отображении линейной функцией. Выполнив один из предложенных приемов, можно построить образ данного прямоугольника при отображении конкретной линейной функцией , например, w= 2iz+2-3i.
Отметим, что в плоскоти uOv свой масштаб. Поэтому, несмотря на то, что прямоугольник при отображении w=2iz+2-3i увеличивается вдвое, это меняет только координаты вершин, что хорошо видно на новом рисунке.
В заключение решения данного примера отметим, что всегда рекомендуется использовать те приемы (качественные и-или количественные), которые проще и быстрее дают результат. Это остается справедливым во всех случаях.
Пример 2. Отображение функцией w= 1z . Сначала отметим, что можно эту функцию записать так w= x +1iy или так w= xx2 ++iyy2 . Отсюда следует, что
25

|
|
|
|
|
|
|
|
|
|
|
|
26 |
|
|
|
x |
|
|
|
∂u |
|
∂v |
|
|
|
u = |
|
|
|
|
, |
|
|
= |
|
, |
|
|
x |
2 |
+ y |
2 |
∂x |
∂y |
|
||||||
|
|
|
|
Легко проверить, что условия аналитичности |
|
|
|
для |
||||
|
|
|
y |
|
|
|
∂u |
= −∂v |
||||
v = |
|
|
|
|
. |
|
|
|||||
|
2 |
|
2 |
|
|
|
||||||
|
x |
+ y |
|
|
|
∂y |
|
∂x |
|
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||
этой функции выполняются во всех точках плоскости z, кроме начала координат (сделайте это самостоятельно). Но началу координат z=0 при таком отображении будет соответствовать ∞-удаленная точка. И, если условиться (договориться дополнительно), что образы всех кривых, которые проходят через ∞-удаленную точку пересекаются там под такими же углами, как и их
прообразы, проходящие через |
z=0 , то |
отображение w= |
1 |
становится |
|
|
|
z |
|
конформным на расширенной |
комплексной |
плоскости @z (плоскости z с |
||
добавленной к ней ∞-удаленной точкой). |
|
|
|
|
Рассмотрим качественный подход в изучении отображения w= 1z .
Легко видеть, что соотношение w= 1z эквиалентно равенствам
| w | | z | =1 и argw= -argz (это следует из геометрического смысла операции деления комплексных чисел) . Второе равенство говорит, что образ w и прообраз z расположены симметрично относительно действительной оси (u или х). Для первого соотношения построим рисунок, известный из школьной
геометрии. |
Внутри окружности радиуса |
|
|||
|
1 |
с |
центром |
в |
|
|
начале |
|
координат |
||
|
|
|
|
возьмем |
|
|
|
произвольную |
|||
|
точку |
z. |
Через |
z |
|
|
проведем луч Оz. В |
||||
|
точке |
z |
восставим |
||
|
перпендикуляр к Oz |
||||
|
до |
пересечения |
с |
||
|
окружностью в |
А. |
|||
|
Через |
А |
проведем |
||
|
касательную |
к |
|||
|
окружности |
до |
|||
|
|
|
пересечения |
||
|
касательной и луча |
||||
Оz в точке В. Через В проведем перпендикуляр к действительной оси (считая совмещенными оси u и х). Остается только из начала координат провести луч, симметричный Оz относительно действительной оси. Перпендикуляр через В и этот луч пересекаются в некоторой точке w. Ниже выяснится, для чего взяты такие обозначения точек z и w. Построение закончено. Сразу обнаруживаются два подобных треугольника : ОАВ и ОАz, т.к. они прямоугольные и имеют
26
27
общий АОВ. Из подобия получаем соотношение OAOz = OBOA . Но по
построению ОВ=Оw, а ОА=1 получаем Oz Ow =1. И в дополнение к этому лучи Оw и Оz симметричны относительно действительной оси. Значит, эти точки удовлетворяют требованию для комплексных чисел | w | | z | =1 и argw= -
argz. Т.е. мы построили точку w как образ точки z при отображении w= 1z .
Точки В и z принято называть симметричными в окружности (зеркально отраженными в “сферическом зеркале”), а точки В и w симметричными в действительной оси (зеркально отраженными в “ плоском зеркале”). Т.е.
отображение w= 1z есть суперпозиция двух последовательных зеркальных отражений – в плоском и сферическом зеркалах.
Получен механизм (алгоритм) отображения w= 1z .
Определение. Суперпозицию двойного отражения в круглом и плоском зеркале принято называть инверсией.
Некоторые свойства инверсии, вытекающие непосредственно из анализа построений. Эти свойства позволяют качественно выяснять расположения
образа фигур при отображении w= 1z .
1.Точкам комплексной плоскости, расположенным внутри единичной окружности, соответствуют точки, расположенные вне окружности и наоборот. 2.Точкам комплексной плоскости, расположенным ниже действительной оси, соответствуют точки, расположенные выше этой оси и наоброт.
3.Точки самой окружности отражаются в действительной оси. При этом две точки (-1;0) и (1;0) остаются неподвижными. (Легко видеть, что неподвижные
точки можно найти, если в соотношении w= 1z принять w=z. Получим решение
уравнения z2=1, откуда z= ±1).
4.Начало координат отображается в ∞-удаленную точку и наоборот. 5.Окружности и прямые (которые, как мы знаем, являются окружностями, проходящими через ∞-удаленную точку – смотри понятие сферы Римана) , которые проходят через начало координат отображаются в прямые, которые проходят через∞-удаленную точку.
Руководствуясь этими свойствами, можно легко и быстро строить образы
геометрических фигур при отображении w= 1 . |
|
||||||
|
|
|
|
z |
|
z |
|
Например, открытый |
полукруг |
|
|
<1, |
(левая часть рисунка) при |
||
|
|
||||||
|
|
|
|
|
|||
|
|
|
|
||||
|
|
Re z > 0 |
|
||||
отображении w= 1z превращается в область, изображенную справа.
27

28
После этого примера можно переходить к более сложному и часто используемому отображению дробно-линейной функцией. И опять используем
качественный подход.
Имеем дробно-линейную функцию w= az +b |
при условии ac ≠bd. |
cz + d |
|
Преобразуем выражение, записанное справа от равенства так : разделим многочлен в числителе на знаменатель “уголком” (как делали это в школе в
младших классах). Получим w= a |
|
b − |
ad |
или так w= a |
|
bc −ad |
|
|
+ |
c |
+ |
c2 |
. Опустим |
||||
cz + d |
d |
|||||||
c |
|
c |
|
|
||||
|
|
|
|
|
|
z + c |
|
|
детали (количественные характеристики) и получим удобную для изучение и анализа форму записи дробно-линейного отображения w= z +Am + B , где А, В и m – некоторые комплексные константы. Из последней записи следует, что
отображение w= |
A |
+ B (а, фактически, w= az +b ) представляет собой |
|
z + m |
|||
|
cz + d |
последовательность (суперпозицию) известных отображений:
-w1=z+m – сдвиг комплексной плоскости z на вектор m; в комплексной плоскости w1 получим первый образ исходной фигуры из плоскости z;
-w2= 1 – инверсия фигуры из плоскости w1 в фигуру комплексной плоскости w1
w2 (отражение в единичной окружности и в действительной оси);
-w=Аw1+В – линейное отображение фигуры из комплексной плоскости w2 в
окончательную фигуру – искомый образ при отображении w= czaz ++db ;
отображение w=Аw1+В = это деформация плоскости w2 в | А | раз с поворотом на угол argA против часовой стрелки и затем перемещение (сдвиг) на вектор В.
28

29
Приемы количественных соотношений при отображении w= az +b cz + d
заключаются в свойствах:
1.Круговое свойство: всякая окружность (прямая) при отображении w= az +b cz + d
переходит в окружность (прямую).
2.Свойство симметрии – пара симметричных относительно единичной окружности точек переходит в пару симметричных точек.
3.Один из параметров a,b,c,d отображения w= czaz ++db может без ущерба быть
исключен (разделив на него числитель и знаменатель, мы получим в одном месте 1). И потому отображение определяется шестью действительными параметрами (по два на каждый комплексный параметр). Поэтому при поиске
нужного отображения w= az +b |
при заданных прообразе D и искомом образе |
||||||||||
|
|
|
|
|
|
|
|
cz + d |
|
||
G достаточно задать 3 пары соответствующих точек на образе и прообразе |
|||||||||||
(z1 w1; z2 w2; z3 w3;). Тогда соотношения |
|||||||||||
|
w − w1 |
= w2 − w3 |
= |
z − z1 |
= |
z2 − z3 |
|
приведут неявно к отысканию нужного |
|||
|
|
|
|
||||||||
|
w − w w − w z − z z |
2 |
− z |
|
|||||||
3 |
2 |
1 |
3 |
|
|
1 |
|
|
|||
w= czaz ++db . В частности, если одна из точек образа или прообраза будет ∞-
удаленной точкой, то отношение (дробь) с ней следует заменить на 1. 4.Существует единственная w= czaz ++db , преобразующая окружность из @z в
заданную окружность на @w так, что 3 заданные точки одной окружности преобразуются в 3 заданные точки другой.
5.Можно найти и неподвижные точки отображения w= czaz ++db , для чего
достаточно решить уравнение z= czaz ++db . Таких точек всегда не более двух (как и корней всякого квадратного уравнения).
9.Если кружность при отображении w= czaz ++db переходит в окружность, то :
либо область изнутри одной окружности переходит в область внутри другой, либо область изнутри одной окружности переходит в область снаружи другой – принцип соответствия границ.
Приведем цифровой пример. Дан полукруг радиуса 1 с центром в начале координат и расположенный выше действительной оси (оси Ох). Требуется
установить образ этой фигуры при отображении w=i11+− zz .
Решение. Сначала преобразуем нашу функцию так w= −zzi++1i = -i+ z2+i1 =
29
30
-i +2i z 1+1. Поэтому заданный нам полукруг следует: сдвинуть вправо вдоль
действительной оси на 1 единицу (см. z+1); полученную фигуру инверсировать (отразить в единичной окружности и в действительной оси); затем растянуть в два раза (см. | 2i |=2) от начала координат, повернуть против часовой стрелки
на угол arg2i= π2 и, наконец, сдвинуть на вектор -i (т.е. вниз на 1). Все это
выводы качественные. Для уточнения деталей используем количественные по ходу построений.
Заданный нам полукруг можно записать так
|
|
z |
|
≤1, |
|
|
|
||||
|
|
|
|
|
|
≤ arg z ≤π. |
|||||
0 |
|||||
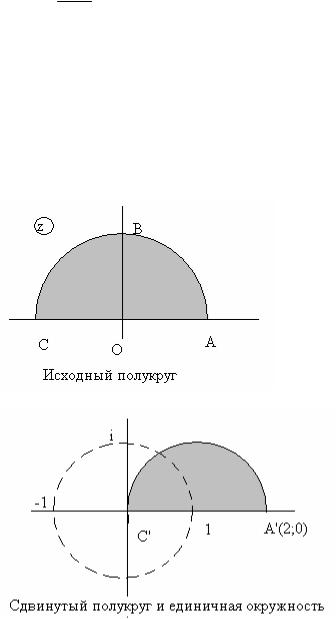
Сдвигаем этот полукруг вправо и в новой комплексной плоскости получаем рисунок сдвинутого полукруга C’O’A’B’.
Никаких количественных соотношений здесь не требуется.
На сдвинутом полукруге изображаем штрихами единичную окружность, в которой будем отражать затененную фигуру. Сначала
рассмотрим только отражение в
окружности.
Точки криволинейного треугольника окажутся снаружи единичной окружности, а точки оставшейся части полукруга окажутся внутри единичной окружности.
Для деталировки уточним расположение точек A’,C’ и точки пересечения единичной окружности и полуокружности границы полукруга при отражении в единичной окружности.
Так точка А’(2;0) останется на действительной оси, но внутри единичной окружности на расстоянии 0,5 от начала координат. Ее образом будет A’’(0,5; 0). Точка C’(0;0) перейдет в ∞-удаленную точку, расположенную далеко справа на действительной оси. Точка пересечения двух окружностей остается на месте. Это значит, что отрезок A’C’ отображается в луч [0,5; ∞) действительной оси.
Теперь предстоит отражение в действительной оси. Легко найти только образ точки пересечения двух окружностей – она отразится в действительной оси и окажется внизу на единичной окружности.
30

31
При завершении инверсии – нам известно, что весь образ окажется под действительной осью. Так как это первый пример на инверсию, то у нас мало опыта и для выяснения вида образа фигуры у нас недостаточно сведний. Поэтому известными приемами выполним следующие преобразования с
1 . Т.к. и w2 и w1 - комплексные, то не будем обращать w1
внимания на индексы, чтобы не путаться и будем говорить везде только про w и z , а все геометрические действия выполнять на одной и той же комплексной плоскости z (как будто рисуем на стекле копию рисунка с бумаги, на которую
стекло |
|
|
положено). |
Тогда |
имеем |
w= 1 |
= |
1 |
= |
x −iy |
= |
|||||||||||
|
|
x +iy |
(x +iy)(x −iy) |
|||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
−y |
|
|
|
z |
|
|
|
|||
= |
|
|
|
|
+i |
|
|
|
|
. Т.е. функция w= 1 может быть записана так |
|
|
||||||||||
x2 |
+ y2 |
x |
2 |
+ y2 |
|
|
||||||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
2 |
+ y |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
(хх) Используем эти соотношения для работы. Найдем образ |
|||||||||||||
|
|
|
|
|
|
−y |
|
|||||||||||||||
v = |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x |
2 |
+ y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отрезка А’С’ при инверсии. Уравнение этого отрезка у=0 и 0≤x ≤2. Двигаемся
|
1 |
, Это – параметрические |
справа-налево. Тогда (хх) принимает вид u = x |
||
v = 0.
(параметр х) уравнения луча [ 0,5; ∞) оси Ou (действительной оси), пробегаемого слева-направо.
Если двигаться по А’С’ на прообразе, то затененная область оказываются справа по ходу движения. Следовательно, образ фигуры должен располагаться справа внизу от луча [ 0,5; ∞) оси Ou.
Теперь переходим к выяснению образа дуги полукруга. Одна из точек образа – точка пересечения окружностей - расположена на единичной окружности и и потому останется на ней, но симметрично относительно действительной оси.. Выясним вид образа дуги А’С’. Для этого запишем уравнение для этой дуги (х-
1)2+у2=1 или проще х2+у2=2х при 0 ≤у≤1. |
При инверсии заданной (хх) из |
||||
|
u = 1 |
, |
|
|
|
этихих условиях получаем |
|
2 |
|
Это луч, параллельный мнимой оси v, |
|
|
|
||||
|
|
−y |
. |
|
|
|
v = |
2x |
|
||
|
|
|
|
||
начинающийся в точке |
А(0,5; |
|
0) и |
направленный перпендикулярно |
|
действительной оси u вниз – к образу точки С’ – т.е. к ∞-удаленной точке. Это в самом деле так, потому что его уравнение u=0,5, а при 0 ≤у≤1 и х>0 видно ,
что v= −2yx остается всегда отрицательно.
31
32
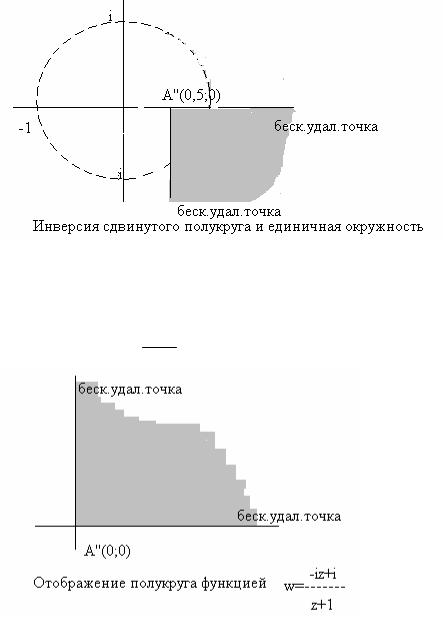
Отметим, что дуга
окружности, проходящей через начало координат отображается в луч,
который проходит через ∞- удаленную точку
Полученный в результате двух последовательных отображений сектор еще предстоит растянуть в 2 раза, повернуть на 90о и сдвинуть на вектор -i=(0;-1) – вниз на 1. Получаем окончательный образ исходного полукруга при
отображении w=i11+− zz .
|
|
|
|
|
|
|
|
|
|
Тех |
же |
результатов |
можно |
|||
|
|
|
|
|
|
|
|
|
|
добиться количественно – т.е. |
||||||
|
|
|
|
|
|
|
|
|
|
непосредственными |
|
|||||
|
|
|
|
|
|
|
|
|
|
вычислениями с |
|
|
||||
|
|
|
|
|
|
|
|
|
|
последующим |
|
указанием |
||||
|
|
|
|
|
|
|
|
|
|
направления |
движения |
вдоль |
||||
|
|
|
|
|
|
|
|
|
|
границ. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Сначала найдем |
|
||||
|
|
|
|
|
|
|
|
|
|
действительную |
и |
мнимую |
||||
|
|
|
|
|
|
|
|
|
|
части для |
w= |
−zi +i . Получаем |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z +1 |
|
||
w= |
−zi +i |
= −(x +iy)i +i = |
y +i(−x +1) |
= |
(y +i(−x +1))((x +1) −iy) = |
|
|
|||||||||
z +1 |
(x +1) +iy |
|
|
|||||||||||||
|
|
|
x +iy +1 |
|
|
((x +1) +iy)((x +1) −iy) |
|
|
|
|||||||
= |
|
2y |
|
+i |
1− x2 |
− y2 |
. (Не приведены |
подробности |
умножений и |
|||||||
(x +1)2 + y2 |
(x +1)2 + y2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
приведения подобных членов. Достигнуто требование: результат должен быть комплексным). Из полученного соотношения следует, что отображению
|
|
|
2 y |
|
|
|
|
|
|
|
u = |
|
|
|
|
, |
|
|
−zi +i |
(x +1) |
2 |
+ y |
2 |
|||
w= |
|
|
|
|
(**) Используем эти |
|||
z +1 |
соответствуют соотношения |
1− x2 − y2 |
|
|
||||
|
v = |
|
|
. |
||||
|
|
|
|
|
|
|
||
|
|
|
(x +1) |
2 |
+ y |
2 |
|
|
|
|
|
|
|
|
|
||
соотношения для работы так. Договоримся двигаться по границе заданного полукруга так, чтобы точки полукруга оставались все время слева по ходу
32

33
движения. Того же потребуем и от движения по границе будущего образа. Найдем образ отрезка CА при отображении (**). Уравнение этого отрезка у=0
|
|
u = 0, |
|
|
|
|
и -1≤x ≤1. Подставим это в (**) и получим |
|
|
1− x2 |
|
|
Или |
|
|
|
|
|||
|
v = |
|
|
|
. |
|
|
|
(x +1) |
2 |
|
||
|
|
|
|
|
|
|
u = 0, |
|
|
|
|
1− x |
|
Получены параметрические уравнения отрезка оси Ov, на котором v |
|
|
||
v = |
|
. |
|
1+ x |
|
||
|
|
|
|
меняется так: точке С(-1; 0) соответствует ∞-удаленная точка; точке О(0;0) соответствует (0;1); точке А(1;0) соответствует ( 0;0). При этом мы двигаемся вдоль оси Ov сверху вниз (от ∞-удаленной точки к началу координат) и точки образа должны находиться слева по ходу движения. Если же мы движемся по дуге АС, то уравнение этой дуги х2+у2=1 при y ≥0. После подстановки его в
|
|
|
|
y |
|
|
|
(**) получим |
u = |
|
|
|
, |
Это уравнение действительной оси Ou как образ дуги |
|
|
x +1 |
||||||
|
|
|
|
||||
|
|
v |
= 0. |
|
|
|
|
|
|
|
|
|
|||
полуокружности х2+у2=1 при y ≥0. Этот образ мы пробегаем от образа точки (0;0) до ∞-удаленной точки, которая служит образом точки С(-1;0) но уже на действительной оси. При таком движении точки образа полукруга располагаются слева по ходу движения. Все это совпадает с ранее полученной картиной.
Естественно, что строгого разделения на количественные и качественные выкладки нет. Каждый шаг выполняют наиболее простым путем. Поэтому в двльнейшем на этом заострять внимания не будем.
Приведем примеры других простых отображений.
Пусть дана комплексная экспонента w=ez. Преобразуем эту функцию и найдем ее действительную и мнимую составляющие. Получаем w=ez=
=eх(cosф+isinф). Откуда |
|
x |
cosô , |
Легко проверить, что w=ez – |
u = e |
|
|||
|
v = ex sin ô . |
|
||
аналитическая функция и потому отображение w=ez – конформно. Но т.к. w=ez= w=ex eiy, то получаем │ w │= │ ez │= ex и argw=arg(ez )=y+2kπ i. Т.е
комплексная функция периодическая с периодом Т=2kπ i. Воспользуемся этим
при построении образа при отображении комплексной экспонентой. |
Начнем |
||
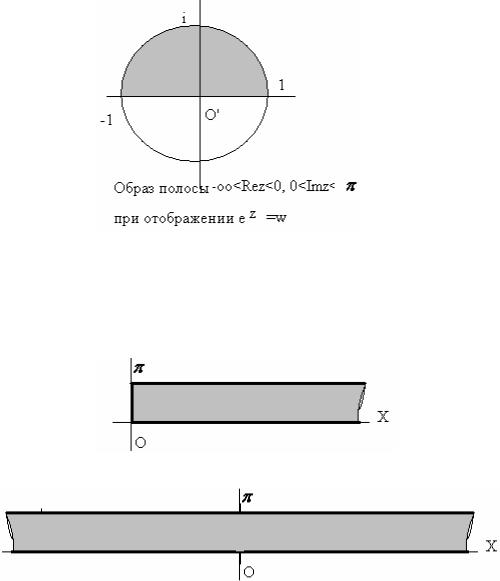
с простого. Выясним, во что отображается полуполоса вида |
|
||
−∞ < Re z ≤ 0, |
при отображении w=ez? |
|
|
|
0 ≤ Im z ≤π |
|
|
|
Решение. |
Построим |
|
|
|
||
|
|
полуполосу |
|
Т.к. Rez=x и −∞ < Re z ≤ 0 , а
33
34
│ w │= │ ez │= ex , то при заданном изменении переменной х величина │ w
│=│ ez │= ex изменяется на промежутке от 0= e−∞ до 1= e0 . Это означает, что образы всех точек полуполосы оказываются расположенными от начала
координат |
не |
далее |
окружности радиуса 1. |
|
А т.к. |
0 ≤ Im z ≤π и Imz=y= |
|
argw=arg(ez |
), |
|
|
|
−∞ < Re z ≤ 0, |
находятся в |
|
то все точки образа полуполосы |
|
||||||
|
|
|
|
|
0 ≤ Im z ≤π |
|
|
верхней половине |
указанной окружности. |
Получаем |
образ полуполосы |
||||
|
|
|
−∞ < Re z ≤ 0, |
при отображении w=ez. |
|||
|
|
|
|
|
|||
|
|
|
0 ≤ Im z ≤π |
|
|
|
|
Отметим, что из количественных выкладок следует: отрезок [0;π ] мнимой оси плоскости z преобразуется в верхнюю часть окружности, т.к. 0 ≤ Im z ≤π при х=0 дает нам уравнение │ w │=1 – т.е.
окружность радиуса 1 и центром в начале координат; промежуток - ∞<Rez ≤0 для
у=0 дает нам участок [O’; 1] действительной оси u плоскости w, а верхняя граница полуполосы при у=π - отображается в отрезок [-1; O’]
действительной оси u плоскости w. Еще скажем, что направления обходов полуполосы и полученного полукруга согласованы.
0 ≤ Re z < ∞,
Если рассматривать другую полуполосу при отображении
0 ≤ Im z ≤π
w=ez,
то легко обнаружить, что образом ей служит внешность такой же окружности.
Если рассматривать полную полосу,
то ее образ при отображении w=ez представляет собой всю комплексную плоскость.
Комментарий. Построенные отображения говорят о том, что их можно использовать при исследовании электрических полей плоских (а в виде отображений и сферических) конденсаторов.
Более сложные задачи на построение отображений аналитическими функциями можно найти в специальной литературе, например, П.Ф.Фильчаков,
34
