
Metodichka_chast_2
.pdfгде x0 – начало медианного интервала (первого из интервалов, у кото-
рого накопленная частота больше половины объема выборки);
h – ширина интервала; n – объем выборки;
n1 – накопленная частота интервала, предшествующего медиан-
ному;
mMe – частота медианного интервала.
Мода Mо(X ) – это значение признака X, которому соответствует наибольшая частота. Моду интервального ряда вычисляют по формуле
Mo( X ) x0 |
h |
|
m0 |
m1 |
, |
|
(m0 |
m1 ) |
(m0 m2 ) |
||||
|
|
|
где x0 – начало модального интервала (интервала с наибольшей ча-
стотой);
h – ширина интервала;
m0 – частота модального интервала;
m1 – частота интервала, предшествующего модальному; m2 – частота интервала, следующего за модальным.
Асимметрия и эксцесс характеризуют отклонение эмпирического распределения от нормального.
Асимметрия есть число, которое определяется по формуле
|
|
1 |
k |
(x x )3 m |
|
|
|
n |
|
||
As |
i в i |
||||
|
|
||||
|
i 1 |
|
|||
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
в |
|
для сгруппированных данных. Для симметричного распределения As 0 . Если As 0 , то в ряду преобладают (имеют большую часто-
ту) значения признака меньшие, чем средняя. Такой ряд является отрицательно асимметричным. Если As 0 , то в ряду преобладают значения признака большие, чем средняя. Такой ряд является положи-
тельно асимметричным.
Эксцессом выборки называется число, которое определяется по формуле
|
|
1 |
k |
(x x )4 m |
|
|
|
n |
|
|
|
|
|
i в i |
|
||
|
|
|
|
|
|
Ex |
|
|
i 1 |
|
3 |
|
|
|
4 |
||
|
|
|
|
|
|
|
|
|
|
в |
|
и характеризует крутизну (заостренность) графика распределения. Для нормального распределения Ex 0 . Если максимум эмпирического
распределения расположен выше, чем у нормального, то эмпирическое
73
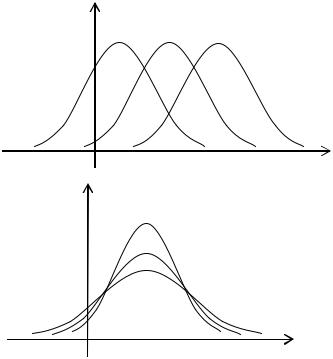
распределение имеет положительный эксцесс, т.е. Ex 0 . Если же максимум эмпирического распределения расположен ниже, чем у нормального, то эмпирическое распределение имеет отрицательный эксцесс, т.е. Ex 0 .
As< 0 |
As = 0 |
As > 0 |
x
Ex > 0 |
|
• |
|
• |
Ex = 0 |
|
|
• |
|
Ex < 0
x
10.4. Точечные и интервальные оценки параметров распределения
Важнейшей задачей математической статистики является задача оценивания (приближенного определения) по выборочным данным параметров закона распределения признака Х генеральной совокупно-
сти. Другими словами, необходимо по данным выборочного распределения оценить неизвестные параметры теоретического распределения.
Статистические оценки могут быть точечными и интервальными. Задачу статистического оценивания рассмотрим для нормального распределения.
74
Пусть признак Х генеральной совокупности распределен нормально, т.е. его теоретическое распределение имеет вид:
|
|
1 |
|
|
|
( x a)2 |
|
|
f (x) |
|
|
e |
2 2 |
, |
|||
|
|
|
||||||
|
|
|
|
|
|
|||
|
2 |
|
|
|||||
где a M (X ) xген – математическое ожидание признака Х;
– среднее квадратическое отклонение признака Х.
Точечной оценкой неизвестного параметра называется число, которое приблизительно равно оцениваемому параметру и может заменить его с достаточной степенью точности в статистических расчетах.
Точечной оценкой генеральной средней xген и параметра а может служить выборочная средняя xв .
В качестве точечной оценки для генеральной дисперсии Dген может
быть использована выборочная дисперсия или, если объем выборки небольшой, исправленная выборочная дисперсия
S 2 |
|
n |
D . |
|
|
||||
|
|
n 1 |
в |
|
|
|
|
||
Для генерального среднего |
квадратического отклонения ген |
|||
точечной оценкой может служить выборочное среднее квадратическое
отклонение |
в |
или исправленное выборочное среднее квадратическое |
||
|
s |
|
|
|
отклонение |
|
S 2 . |
||
Для того, чтобы точечные статистические оценки обеспечивали хорошие приближения неизвестных параметров, они должны быть
несмещенными, состоятельными и эффективными.
Обозначим через неизвестный параметр, а через * – его точечную оценку.
Несмещенной называется такая точечная статистическая оценка* , математическое ожидание которой равно оцениваемому парамет-
ру: M ( * ) .
Состоятельной называется такая точечная статистическая оценка, которая при n стремится по вероятности к оцениваемому параметру.
Эффективной называется такая точечная статистическая оценка, которая при фиксированном объеме выборки имеет наименьшую дисперсию.
Выборочная средняя xв обладает всеми этими свойствами, т.е. является несмещенной, состоятельной и эффективной оценкой генеральной средней xген .
75

При использовании точечной оценки неизвестного параметра мы не знаем, какая совершается ошибка, если вместо точного значения этого параметра используется его приближенное значение. Поэтому во многих случаях имеет смысл пользоваться интервальной оценкой. Суть такой оценки состоит в том, что определяется некоторый интервал, внутри которого с определенной вероятностью находится неизвестное значение параметра .
Доверительной вероятностью оценки называется вероятность p 1 выполнения неравенства * , где – точность оцен-
ки, т.е. P * 1 .
Обычно доверительная вероятность задается заранее, при этом наиболее часто полагают 1 равным 0,90, 0,95, 0,99 . Число назы-
вается уровнем значимости.
Из определения доверительной вероятности можно записать
P( * * ) 1 .
Это означает, что с вероятностью 1 неизвестный параметр находится внутри интервала ( * ; * ) . Доверительную вероятность называют надежностью, с которой оцениваемый параметр покрывается интервалом ( * ; * ) .
Доверительным интервалом называется интервал ( * ; * ) ,
накрывающий неизвестный параметр с заданной вероятностью 1 . Границы доверительного интервала называются доверитель-
ными границами.
В прикладных статистических задачах длина доверительного ин-
тервала играет важную роль: чем меньше его длина, тем точнее оцен-
ка. Если длина доверительного интервала велика, то ценность такой оценки незначительна.
10.5. Элементы корреляционного и регрессионного анализа
Одной из важнейших задач математической статистики является нахождение зависимостей между переменными Х и Y. В естественных науках большей частью приходится сталкиваться с зависимостями, когда каждому значению одной величины строго соответствует определенное значение другой величины. Такие зависимости называются
функциональными.
В большинстве случаев между переменными, характеризующими экономические показатели, существуют зависимости, отличные от функциональных. Зависимости между переменными, когда каждому
76
значению переменной Х соответствует не одно, а множество возможных значений переменной Y, называются стохастическими или корреляционными. Эти зависимости обнаруживаются лишь при массовом изучении переменных.
Например, уровень производительности труда Y на предприятиях тем выше, чем больше его электровооруженность X. Вместе с тем такая зависимость может быть не обязательно однозначной. И это потому, что зависимая переменная Y испытывает влияние не только переменной Х, но и целого ряда других факторов, которые не учитываются. Кроме этого, влияние выделенного фактора может быть не прямым, а проявляться через цепочку других факторов. Поэтому в таких зависимостях каждому значению независимой переменной Х может соответствовать не одно, а ряд значений переменной Y.
При изучении корреляционных зависимостей ( связей) возникают два основных вопроса – о тесноте связи и о форме связи. Если рассматриваются только две переменные, то связь (корреляция) между ними называется парной.
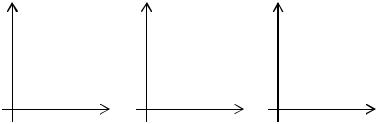
Если с увеличением значений переменной Х значения переменной Y в среднем растут, то такая парная корреляция называется положительной. Если же с ростом значений переменной Х значения переменной Y в среднем уменьшаются, то такая корреляция называется отрицательной. Если же между переменными Х и Y связь отсутствует, то говорят, что имеет место нулевая корреляция.
Каждую пару значений (xi ; yi ) , соответствующих значениям пе-
ременных X и Y в i-м наблюдении, можно изобразить в виде точки на координатной плоскости. Совокупность таких точек называется кор-
реляционным полем.
y |
y |
y |
x |
x |
x |
Линейная корреляционная зависимость и прямые регрессии.
Ранее было отмечено, что корреляция по направлению может быть положительной и отрицательной. Положительную корреляцию называют прямой, а отрицательную – обратной. По форме корреляция может быть линейной и криволинейной.
77
Парная корреляционная зависимость будет линейной, если она приближенно выражается линейной функцией.
y |
|
|
|
y |
y |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
• |
• |
• |
|
|
|
• |
• |
• |
• • |
• |
|
|
|
|
• • |
|
|
|||
• |
• • |
• |
|
• |
• |
|
|
• • |
• |
|
|
• • |
• |
• |
• |
• |
|
|
|
• • |
|
• |
• • • |
x |
x |
x |
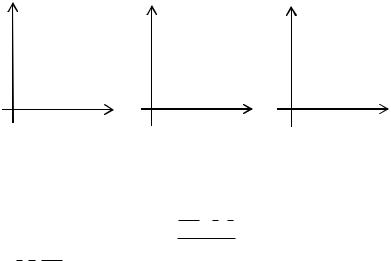
Линейная прямая |
Линейная обратная |
Криволинейная |
Вид зависимости можно определить по виду корреляционного поля, т.е. по расположению построенных точек подбирается линия. Если это будет прямая, то корреляция между признаками будет линейной.
Для оценки тесноты связи между признаками используется выборочный линейный коэффициент корреляции
rв x y x y ,
x y
где x, y, x y – выборочные средние;
x , y – выборочные средние квадратические отклонения.
Так как коэффициент корреляции rв определяется по выборочным данным, то он является оценкой генерального коэффициента кор-
реляции rген .
Коэффициент корреляции находится в пределах от –1 до 1, т.е.1 rв 1. Чем ближе rв к –1 или 1, тем теснее связь между перемен-
ными Х и Y. Чем ближе rв к нулю, тем слабее связь между перемен-
ными. Таким образом, по величине коэффициента корреляции можно судить о тесноте связи между двумя переменными.
По знаку коэффициента корреляции можно судить о направлении корреляционной зависимости между переменными Х и Y. Если rв 0 ,
то зависимость прямая. Если же rв 0 , то зависимость обратная.
Квадрат коэффициента корреляции rв 2 называется коэффициен-
том детерминации и обозначается D rв 2 в долях или D rв 2 100%
в процентах. Он показывает, на сколько процентов в среднем изменения зависимой переменной Y зависят от независимой переменной Х.
78
Линейная корреляционная зависимость между переменными Х и Y приближенно выражается в виде линейного уравнения
Y aX b .
Это уравнение называется уравнением регрессии Y на Х, а его график называется линией регрессии. Если уравнение регрессии описывает зависимость между двумя переменными, то такая регрессия называет-
ся парной.
10.6. Метод наименьших квадратов
Неизвестные параметры a и b уравнения линейной регрессии находятся методом наименьших квадратов. Применяя этот метод, получим систему нормальных уравнений
a n xi2
i 1n
a xii 1
n |
n |
b xi xi yi , |
|
i 1 |
i 1 |
bn yi .
i 1n
Решив систему, найдем a и b. Параметр a называется коэффициентом регрессии. Он показывает, как изменится в среднем функция Y, если аргумент Х изменится на единицу своего измерения.
Уравнение регрессии – наиболее часто встречающийся в практике вид статистической модели. Подобные модели применяются для экономического и технико-экономического анализа, где с помощью уравнений регрессии измеряют влияние отдельных факторов на зависимую переменную. Тем самым анализ становится более конкретным, а его познавательная ценность значительно увеличивается. Кроме этого, уравнения регрессии применяются при прогнозировании.
Пример 1. Изучается зависимость себестоимости одного изделия (Y, у.е.) от величины выпуска продукции (Х, тыс. шт.) по группе предприятий за отчетный период. Получены следующие данные:
Х |
2 |
3 |
4 |
5 |
6 |
Y |
1,9 |
1,7 |
1,8 |
1,6 |
1,4 |
Провести корреляционно-регрессионный анализ зависимости себестоимости одного изделия от выпуска продукции.
Построим корреляционное поле. По корреляционному полю определяем, что зависимость между себестоимостью одного изделия и выпуском продукции близка к линейной. В этом случае уравнение ре-
грессии имеет вид Y aX b .
79
У |
|
|
1,9 |
• |
|
1,8 |
• |
|
1,7 |
• |
|
1,6 |
||
• |
||
1,5 |
||
|
||
1,4 |
|
|
1,3 |
• |
1 |
2 |
3 |
4 |
5 |
6 |
Х |
|
Выполним все необходимые вычисления и запишем в виде таблицы:
№ п/п |
xi |
yi |
xi yi |
2 |
|
xi |
|||
1 |
2 |
1,9 |
3,8 |
4 |
2 |
3 |
1,7 |
5,1 |
9 |
3 |
4 |
1,8 |
7,2 |
16 |
4 |
5 |
1,6 |
8,0 |
25 |
5 |
6 |
1,4 |
8,4 |
36 |
Сумма |
20 |
8,4 |
32,5 |
90 |
|
|
|
|
|
|
n |
|
|
n |
|
|
n |
|
|
|
|
В |
|
данном примере |
xi |
20 , |
yi |
8,4 , |
xi yi |
32,5 , |
||||||||
|
|
|
|
|
|
i 1 |
|
|
i 1 |
|
|
i 1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 . Найдем |
|
4 , |
y 1,68 , xy 6,5 , |
x |
2 , y |
|
0,03 . |
|||||||||
x |
||||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим выборочный коэффициент корреляции rв 0,9 . |
Так как |
|||||||||||||||
|
0,9 |
|
||||||||||||||
коэффициент корреляции |
rв |
близок к единице, то себестоимость |
||||||||||||||
одного изделия и объем выпускаемой продукции находятся в тесной корреляционной зависимости. Коэффициент детерминации равен
D rв 2 100% 81% , т.е. себестоимость единицы продукции на 81%
зависит от объема выпускаемой продукции и на 19% зависит от других факторов.
Для вычисления параметров a и b уравнения регрессии результаты вычислений из таблицы подставим в нормальную систему
80

|
n |
n |
n |
a xi2 b xi |
xi yi , |
||
i 1 |
i 1 |
i 1 |
|
|
n |
n |
|
|
bn yi . |
||
a xi |
|||
|
i 1 |
i 1 |
|
и получим систему уравнений
90a 20b 32,5,20a 5b 8,4,
из которой найдем а= –0,11, b=2,12. Таким образом, уравнение регрессии имеет вид Y 0,11X 2,12 . Из этого уравнения следует, что с уве-
личением выпуска продукции на 1 тыс. шт. себестоимость одного изделия снизится на 0,11 у.е. Если выпуск продукции составит, например, 5.2 тыс. шт., то можно определить себестоимость одного изделия:
Y 0,11 5,2 2,12 1,55 (у.е.).
11. ТИПОВОЙ ПРИМЕР ВЫПОЛНЕНИЯ РАСЧЕТНО-ГРАФИЧЕСКИХ ЗАДАНИЙ ПО ТЕМЕ «ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ»
Пример 1. В таблице приведены данные по бонитировки почв сельскохозяйственных угодий районов Республики Беларусь.
31 |
36 |
34 |
35 |
41 |
44 |
44 |
35 |
34 |
39 |
40 |
40 |
34 |
48 |
37 |
44 |
39 |
41 |
32 |
38 |
36 |
37 |
39 |
38 |
37 |
34 |
44 |
41 |
34 |
35 |
33 |
30 |
40 |
41 |
40 |
43 |
36 |
30 |
35 |
36 |
35 |
45 |
37 |
33 |
34 |
35 |
34 |
36 |
35 |
36 |
На основании статистических данных требуется:
1)составить интервальные статистические ряды распределения частот и относительных частот;
2)построить гистограмму и полигон частот;
3)вычислить числовые характеристики выборки: выборочную
среднюю xв , моду Мо(Х), медиану Мe(Х), выборочную дисперсию Dв, выборочное среднее квадратическое отклонение в .
Решение.
1. Построение интервального вариационного ряда начинается с разбиения интервала изменения случайной величины на k частичных интервалов одинаковой ширины и подсчета частот попадания случайной величины в каждый из этих интервалов.
Для определения числа интервалов k можно пользоваться формулой
k 1 3,2lg(n),
81

где n – объем выборки.
При n=50 получаем k=1+3,2∙lg(50)≈7.
Определим границы интервалов. Для этого находим размах выборки R:
R= xmax – xmin.
Внашем случае xmax= 48, xmin = 30, R =48–30=18.
Обычно начало интервала выбирают на 1 ширины интервала ле-
2
вее xmin, а конец последнего на 1 ширины интервала правее xmax. То-
2
гда ширина интервала определяется по формуле
h xmax xmin .
k 1
Границы интервала находятся следующим образом:
a0 xmin h2 ; a1 a0 h; a2 a1 h;...; an an 1 h .
В качестве контроля должно выполняться равенство an xmax h2 .
В нашем случае h 186 3. Тогда
a0=30–1,5=28,5; a1=28,5+3=31,5; a2=31,5+3=34,5; a3=34,5+3=37,5; a4=37,5+3=40,5; a5=40,5+3=43,5; a6=43,5+3=46,5; a7=46,5+3=49,5.
Составим статистические ряды распределения частот и относительных частот.
Интервалы |
Подсчет ча- |
Частоты |
Относительные |
значений СВ Х |
стот |
mi |
частоты Wi mi / n |
[28,5; 31,5) |
III |
3 |
0,06 |
[31,5; 34,5) |
IIIIIIIIII |
10 |
0,2 |
[34,5; 37,5) |
IIIIIIIIIIIIIIIII |
17 |
0,34 |
[37,5; 40,5) |
IIIIIIIII |
9 |
0,18 |
[40,5; 43,5) |
IIIII |
5 |
0,1 |
[43,5; 46,5) |
IIIII |
5 |
0,1 |
[46,5; 49,5) |
I |
1 |
0,02 |
При подсчете частот в каждый интервал включаются те значения Х, которые больше или равны нижней границы и меньше верхней границе соответствующего интервала. Сумма всех частот должна равняться объему выборки (n=50). Для нахождения относительных частот нужно частоты разделить на объем выборки:
82
