Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусская государственная сельскохозяйственная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Metodichka_chast_2

.pdf

Скачиваний:

Добавлен:

29.02.2016

Размер:

3.33 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

y x2 ,

x x2 2 , x2 x 2 0 , D 1 8 9 ,

x y 2,

1 3

x 1, x 2 .

1,2

Например,

из первого

уравнения системы находим: y

(x )2 1,

(x )2

4 . Таким образом, парабола и прямая пересекаются в двух

точках с координатами

(1; 1)

и ( 2; 4) , одна из которых B(1; 1)

при-

надлежит границе области D .

Внешнее интегрирование по переменной y.

Область интегрирования D

расположена между прямыми

y 0 ,

y 1, а переменная x

изменяется в данной области при каждом фик-

от точек параболы x

сированном значении

y до точек прямой

x 2 y (рис. 4). Следовательно,

2 y

f x, y dxdy dy

f x, y dx .

Внешнее интегрирование по переменной x.

Так как верхний участок границы OBA области

D задан двумя ли-

ниями OB и BA, то прямая x 1 разбивает область D на области D1 :

0 x 1,	0 y x2	и D : 1 x 2 ,		0 y 2 x . В результате получа-
		2
ем сумму двух повторных интегралов:
		1	x2	2	2 x
	f x, y dxdy dx f x, y dy dx f x, y dy .
	D	0	0	1	0

Пример 2. Вычислить двойной интеграл x dxdy , если область

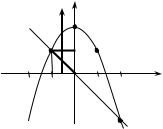
Dограничена линиями x 0 , y x , y 2 x2 . Решение. Построим область D (рис. 5).

y x,

Найдем точки пересечения линий из системы уравнений

y 2 x2 ,

x 2 x2 ,		x2 x 2 0 ,		D 1 8 9 ,
x	1 3		x 2 ,	x 1 .

1,2	2		1	2

			33

Таким образом,				A( 1; 1)						–	точка пересечения линий в рассматрива-
емой области.
Область интегрирования											D расположена между прямыми																		x 1,
x 0 , снизу ограничена прямой y x , сверху – параболой																											x2 2 y
(рис. 5).													y
													y
															2
										A				1
											–1	0						2				x
													Рис. 5
Следовательно,
					0		2 x2					0								0
x dxdy			dx					x dy				xy				2 x x2	dx		x 2 x2 x dx
																	dx

D					1			x				1								1
0									0													2x2	x4			x3		0
																												0

		2												3			2
x 2 x x dx 2x x x dx
x 2 x x dx 2x x x dx																						2	4			3
1									1													2	4			3		1
1									1																			1
		2						4			3							1			1			3			4
		2				( 1)				( 1)
0	( 1)				4				3					1								1
					4				3									4 3						12 12
														7				5
										1										.
										1										.
														12				12
Если проводить внешнее интегрирование по переменной																												y , то об-
ласть D необходимо разбивать на две области прямой																									y 1 и считать
не один, а сумму двух повторных интегралов.

6.3. Приложения двойного интеграла к задачам геометрии и механики

1) Площадь плоской фигуры, занимающей область D , вычисляется по формуле

S dxdy .

2) Объем V тела, ограниченного сверху поверхностью z=f(x, y), снизу – плоскостью z=0 и цилиндрической поверхностью с образующей, параллельной оси Oz, можно найти по формуле

V f x, y dxdy .

		D
3) Площадь поверхности z=f(x,				y),	которая проектируется на
область D плоскости xOy, вычисляется по формуле

Q		z	2		z	2


	1					dxdy .
	1					dxdy .
D		x			y

4) Масса пластинки с поверхностной плотностью (x, y) , занимающей область D плоскости xOy, вычисляется по формуле

m ρ(x, y)dxdy .

5) Статические моменты относительно осей Ox и Oy плоской пластинки D с поверхностной плотностью (x, y) , вычисляются по

формулам

M x y x, y dxdy ,	M y x x, y dxdy .
D	D

6) Координаты центра масс плоской пластинки D с поверхностной плотностью (x, y), вычисляются по формулам

	M y	x x, y dxdy				M		y x, y dxdy
x	M y	D	,	y		M	x	D
c	m	m			c	m		m
	m	m				m		m

где M x , M y – статические моменты пластинки относительно осей Ox

и Oy соответственно, m – масса пластинки.

Пример 1. Вычислить площадь фигуры, ограниченной прямой y 2x 1 и параболой y x 2 1.

Решение. Найдем точки пересечения линий из системы уравнений:

y 2x 1,			x) 0	x1	0, x2	2.
		x(2
y x	2	1,

Построим область интегрирования D (рис. 6).

5 y 2x 1

									y x 2			1
							1
							0	1		2		x
								1		2
								Рис. 6
						2	2 x 1	2					2
Тогда S dxdy dx							dy dx y				x2	1	2x 1 x				1 dx
											2 x 1					2
				D		0	x2 1	0					0
				D		0	x2 1	0					0
	x	3	2	4
		3	2
x2					.
x2					.
	3		3
	3		3
			0
Пример 2. Найти массу плоской пластинки D с поверхностной
плотностью (x, y) 2y ,															y
плотностью (x, y) 2y ,							ограниченной					линиями			y			x , x 0,
y 2 .
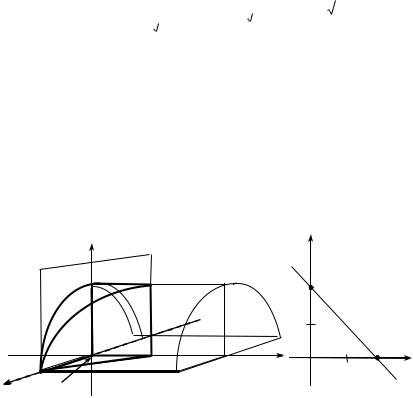
Решение. Построим область интегрирования (рис. 7).
Массу пластинки найдем по формуле										m (x, y)dxdy 2 y dxdy .
												D						D

Область D задается неравенствами: 0 x 4,														x y 2 .
						y
						2	y 2
						1	y
						1	y		x
						0	1 2	3		4			x
								Рис. 7
Следовательно,
								36

			4		2			4						4						2
										2	2	x
										2	2

m	D	2 y dxdy	0	dx			2 y dy	0	dx y					0		dx 4			x

						x
	4		4				4						x2		4
	4		4				4								4

																16 8		8 .
	4 x dx 4dx xdx 4x											2				16 8		8 .
	0		0				0					2			0
	0		0				0								0
Пример 3. Вычислить объем тела V, ограниченного поверхностями
z 4 x2 , x y 2 , x 0,							y 0, z 0.
Решение. Данное тело V ограничено параболическим цилиндром
z 4 x2	с образующей,						параллельной						оси			Oy	и	плоскостями
x y 2 ,	x 0, y 0,		z 0 (рис. 8).

Проекцией тела V на плоскости xOy является треугольник (рис. 9).

Область	интегрирования					D	задается неравенствами:															0 x 2,
0 y 2 x .
			z													y
			z
x y 2						z 4 x2
			4			z 4 x2
			4
															2
																					y 2 x
															1				D
			0																D
			0
				2									y		0						1			2	x
2 D															0						1			2
2 D
x
			Рис. 8																	Рис. 9
Тогда
							2 2 x								2									2 x
																								2 x

V zdxdy 4 x2 dxdy dx									dy 4 x2									4 x2			dx y
D			D				0		0						0									0
2			2												x3				x2			x4	2	0



		2				2		3
										8x 2							4

4 x 2 x dx 8 2x 4x x dx
0			0												3				2			4	0
			16 2		8	4 2 4 12					16			20		.
			16 2		3	4 2 4 12						3				.
					3							3			3
							37

6.4. Криволинейный интеграл по координатам (второго рода)

Рассмотрим на плоскости xOy ориентированную гладкую дугу L (т. е. на дуге L указано направление и в каждой точке существует касательная). Пусть на L определена и непрерывна вектор-функция a P(x, y)i Q(x, y) j .

Разобьем дугу L на n элементарных дуг l1, l2 , , ln и построим век-


торы lk xk i			yk j ,	направленные из начала в конец дуги		lk . На
каждой	элементарной			дуге lk	выберем произвольную	точку
Mk (xk ;	yk )	(рис. 10)		и составим	сумму скалярных произведений

a(xk , yk ) lk :

k 1

a(xk , yk ) lk (P(xk , yk ) xk Q(xk , yk ) yk ),

k 1

которая называется n-ой интегральной суммой.

M k (xk ; yk )

lk ln

Рис. 10

Предел последовательности интегральных сумм In при условии, что max l k 0 , называется криволинейным интегралом по коорди-

натам (второго рода) и обозначается

		P(x,y)dx Q(x,y)dy .
a	dl	P(x,y)dx Q(x,y)dy .
L		L

Аналогично вводится определение криволинейного интеграла от


вектор-функции a(x, y, z) P(x, y, z)i							Q(x, y, z) j		R(x, y, z)k , по про-
странственной дуге L :
		P x,y,z dx			Q x,y,z dy			R x,y,z dz
a	dl	P x,y,z dx			Q x,y,z dy			R x,y,z dz
L		L
				n
			lim			a xk ,yk ,zk		lk .
			max\| lk\| 0
				k 1
						38

Свойства криволинейного интеграла аналогичны свойствам определенного интеграла. В частности, из определения следует, что


a	dl	a

dl ,

т. е. при изменении направления пути интегрирования криволинейный интеграл меняет знак.

Механический смысл криволинейного интеграла

Пусть тело под действием переменной силы


	F P(x, y, z)i		Q(x, y, z) j	R(x, y, z)k
движется по дуге кривой L . Тогда работа				A этой силы может быть
вычислена по формуле
		P x,y,z dx Q x,y,z dy R x,y,z dz .
A F	dl	P x,y,z dx Q x,y,z dy R x,y,z dz .

6.5.Вычисление криволинейного интеграла по координатам

Вычисление криволинейного интеграла сводится к вычислению соответствующего определенного интеграла следующим образом.

1) Если пространственная дуга L задана параметрическими уравне-

ниями x x(t), y y(t), z z(t) , t [ , ] , то

P x,y,z dx Q x,y,z dy R x,y,z dz

P(x(t), y(t), z(t))x (t) Q(x(t), y(t), z(t)) y (t) R(x(t), y(t), z(t))z (t) dt

2) В частности, если плоская дуга L задана уравнением y y(x) , x [a, b] , то

			b

P(x, y)dx Q(x, y)dy P(x, y(x)) Q(x, y(x)) y (x) dx .
L			a
Пример 1. Вычислить xydx (x2 y)dy , если L:
		L
1) дуга параболы	y	x2	1, расположенная между точками A(0; 1)
1) дуга параболы	y		1, расположенная между точками A(0; 1)
	2

иB(2; 3) ;

2)отрезок прямой AB . Решение.

1) Сведем вычисление криволинейного интеграла к определенному,


				x	2							x	2
полагая y				x				1,				x												0 x								2 .
полагая y			2					1,		dy		2		1 dx xdx ,										0 x								2 .
			2									2
												2						x	2													x		2
Тогда xydx x								2	y dy									x									2					x
Тогда xydx x									y dy					x			2				1 dx			x									2		1 xdx
	L																2																2
	L											0
	2 x3								3 3						2					3								x4							2	2
	2 x3								3 3						2					3								x4							2	2

				x						x x dx					2x 2x dx 2																	x					8 4 12.
0		2							2						0														4								0
0															0																						0
2) Запишем уравнение прямой, проходящей через точки A и B :
	x xA								y yA							x 0							y 1	;		x							y 1				; y x 1 .
	xB xA							yB yA								2 0							3 1		2									2
Следовательно,
xydx x2			y dy																											2			x x 1 dx x2								x 1 dx
											y x 1,dy dx,0 x 2
											y x 1,dy dx,0 x 2

L																														0
		2																x3							2					16								34
																									2

							2															2
		2x 2x 1 dx																			x x													4 2						.
		2x 2x 1 dx													2		3				x x									3				4 2				3		.
		0															3								0					3								3
		0																							0

Пример 2. Вычислить работу силового поля																																		F	y2i 2xj						при пе-
ремещении						материальной										точки							вдоль								контура								окружности

x2 y2 4, пробегаемой против часовой стрелки.

Решение.	Запишем	параметрические			уравнения окружности:
x 2 cos(t),	y 2sin(t),	0 t 2 (т.к.		обход		окружности ведется
					Fx ;	Fy найдем по фор-
против часовой стрелки). Работу А силы				F	Fx ;	Fy найдем по фор-

муле: A F	dl Fx dx Fy dy y2dx 2xdy
L	L		L
	x 2cos(t),		dx 2sin(t)dt,		0 t 2π
	x 2cos(t),		dx 2sin(t)dt,		0 t 2π
	y 2sin(t),		dy 2cos(t)dt
	y 2sin(t),		dy 2cos(t)dt
2					2π			2π
(2sin(t))2 ( 2sin(t))dt 2 2cos(t) 2cos(t)dt 8 sin2 (t)d cos(t) 8 cos 2 (t)dt
0					0		0
	2		2π
	8 (1 cos2 (t))d cos(t) 4 1 cos(2t) dt
	0		0
			40

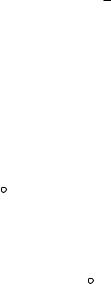
	8
8cos(t)		cos
8cos(t)		cos
	3
	3

8(1 1) 83

3		1		2

	(t) 4t 4		sin(2t)

		2		0

(1 1) 4 2 0 8 .

6.6. Формула Грина. Независимость криволинейного интеграла от линии интегрирования

Формула Грина устанавливает связь между криволинейным интегралом по замкнутому контуру и двойным интегралом по области, ограниченной этим контуром.

Если функции P(x, y), Q(x, y) непрерывны вместе со своими частными производными в некоторой замкнутой области D с границей L,

то справедлива следующая формула Грина:
			Q(x,y)		P(x,y)
	P(x,y)dx Q(x,y)dy
				x	y	dxdy
L			D
где замкнутый контур L обходится против часовой стрелки.
Пусть функции		P(x, y), Q(x, y)		непрерывны		вместе со своими

частными производными в односвязной области D. Для того, чтобы криволинейный интеграл P x,y dx Q x,y) dy не зависел от пути ин-

тегрирования, целиком лежащем в области D, необходимо и доста-

точно, чтобы во всех точках этой области						выполнялось	равенство
P(x, y)	Q(x, y) .	Если	выполняется		это	условие, то	выражение
y	x
P(x, y)dx Q(x, y)dy		представляет собой полный дифференциал неко-
торой функции u, т.е.
	du(x, y) P(x, y)dx Q(x, y)dy .
Эту функцию u(x, y)		можно найти по следующей формуле
		x		y
			P(x, y0 )dx		Q(x, y)dy C,
				y0
		x0		y0
	u(x, y)			y
		x		y
		P(x, y)dx Q(x0 , y)dy C.
		x0	y0

где C – произвольная постоянная.

Начальную точку M0 (x0 ; y0 )			следует выбирать так, чтобы подын-
тегральные функции P(x, y)		и Q(x, y) были определены в этой точке.
Пример 1. Вычислить 2xy y dx x2dy,					где L –	контур		тре-
	L
угольника АBC с вершинами в точках А(–1; 0), В(0; 2), С(1; 0) (рис. 11).
Решение. Поскольку контур является замкнутым,						y
применим формулу	Грина	с	учетом	того,	что		B
						2
P(x, y) 2xy y, Q(x, y) x2 , P			2x 1,	Q 2x.

		y		x
Следовательно,
(2xy y)dx x2dy 2x 2x 1 dxdy					A			C
L					–1	0		1 x
dxdy S 1 AC OB		1 2 2 2 .
						Рис. 11
2		2
Пример 2. Найти функцию u(x, y) по ее полному дифференциалу:

du(x, y)

ln y dx

dy.

Решение. Выберем за начальную точку M0 (1;1) . Получим

y x

u(x, y)

ln y

dy C

x 1, y

1 x2

(

ln(1))dx

dy C (arctg( x) ln(x))|x x ln(y)|y C

1 y

arctg( x) ln(x) arctg(1) x ln(y) C.

Поскольку C arctg(1) также является постоянной, то окончательный ответ можно записать в виде u(x, y) arctg( x) ln(x) xln(y) C.

7. ЗАДАНИЯ, РЕКОМЕНДУЕМЫЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

ПО ТЕМЕ «ДВОЙНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ»

1. В двойном интеграле f x, y dxdy расставить пределы интегриро-

вания двумя способами, если область D ограничена линиями y x2 , y x 2 , x 0 x 0 .

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.02.2016155.39 Кб94makroekonomika 3 k 6 c.pdf
#
29.02.20161.59 Mб20Makroekonomika — копия.pdf
#
29.02.20165.13 Mб192matem.doc
#
28.09.2019164.35 Кб18materialka_otvety_shporka_na_pechat.doc
#
29.02.2016562.18 Кб12metodichka.doc
#
29.02.20163.33 Mб20Metodichka_chast_2.pdf
#
29.02.2016900.1 Кб87Metodichka_MKhZ.doc
#
29.02.2016274.43 Кб67Metodichka_trudovoe_pravo_2.doc
#
12.09.2019559.62 Кб9Metodich_rekomendatsii_po_studencheskim_rabotam...doc
#
29.02.20161.12 Mб37METOD_PO_KURSOV_RAB_posle_red_Konstantinovym.doc
#
29.02.20161.3 Mб66METOD_PO_KURSOV_RAB_posle_red_Konstantinovym.doc