
Metodichka_chast_2
.pdf
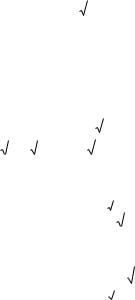
Уравнение прямой |
y x 2 0 за- |
|
у |
|
|
|
|||
|
|
|
|
|
|||||
пишем в виде y x 2 |
. Изобразим эти |
• |
|
• |
|
|
|||
линии в системе координат и найдем |
–2 0 |
2 |
х |
||||||
–3 |
|
||||||||
площадь заштрихованной фигуры. |
|
|
|
|
|
||||
Найдем абсциссы точек пересечения |
|
• |
|
|
|
||||
линий: |
x 2 x 6 x 2 , |
x 2 4 0 , |
|
|
|
|
|||
|
|
|
|
|
|||||
x1 2 , |
x2 2 . |
|
|
|
• |
|
|
|
|
Тогда площадь заштрихованной фигуры равна |
|
|
|
|
|||||
|
|
2 |
x 2 x2 x 6 dx |
|
2 |
||||
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
2 |
||
|
23 |
|
|
|
|
( 2)3 |
|
|
|
|
|
|
|
|
|
|
4 ( 2) |
|
|
|
|
|
|
||||||
3 |
|
4 2 |
3 |
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
3 |
|
|
|
2 |
|
2 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x 4 dx |
3 |
4x |
|||||||||
|
|
|
|
|
|
|
|
2 |
|||
|
8 |
8 |
8 |
8 10 |
2 |
(кв. ед.). |
|||||
3 |
3 |
3 |
|||||||||
|
|
|
|
|
|
|
|
||||
3. ЗАДАНИЯ, РЕКОМЕНДУЕМЫЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ПО ТЕМЕ
«ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ»
1) Найти неопределенные интегралы непосредственным интегрированием:
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
4 |
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||
а) |
|
4x |
|
|
|
|
|
|
3sin(x) 1 dx |
; |
б) |
6x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 dx ; |
||||||||||||||||||||
|
|
x |
4 |
|
|
|
x |
5 |
|
|
1 x |
2 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
в) |
|
4 |
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
x |
|||||||||||||||||||||||||||
5x |
|
|
x |
3 |
|
|
2 |
(x) |
5 dx ; г) |
|
|
|
x |
2 |
|
dx ; |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
д) |
|
2x |
|
|
x |
|
xex |
|
dx ; е) |
cos3 (x) 85 |
|
x3 |
|
3 |
dx . |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
2 |
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2) |
Найти неопределенные интегралы, |
используя метод замены |
|||||||||||||||||||||||||||||||||||||||||||||||||
переменной: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(3x 4)100 dx ; |
|
cos(7x 3)dx ; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
а) |
б) |
в) |
|
|
|
|
2x 3dx ; |
||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
ж) |
|
ectg( x) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
г) |
|
dx ; |
д) x |
x2 |
5dx ; |
|
|
е) |
x2ex |
4dx ; |
|
dx ; |
|||||||||||||||||||||||||||||||||||||||
7 3x |
|
sin2 (x) |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
з) |
|
|
|
dx ; и) |
4 |
|
ln x 1 |
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x2 6x 1 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) Найти неопределенные интегралы интегрированием по частям:
а) |
xe 2x dx ; |
б) |
x ln(x 1)dx ; |
в) |
|
arctg (x)dx ; г) |
arcsin( x)dx; |
|||||||||||||||||||||||||||||
|
|
ln(x) |
dx ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
д) |
е) |
x ln(x)dx . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
4) |
Найти интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
а) |
sin2 (3x)dx ; |
б) |
cos 4 (x)dx ; |
|
в) |
cos 2 (x)sin2 (x)dx ; |
||||||||||||||||||||||||||||||
г) |
cos3 (x) sin2 (x)dx ; д) |
|
|
x 3 |
|
dx ; |
е) |
|
2x 7 |
dx ; |
||||||||||||||||||||||||||
x |
2 |
x |
2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|||||
ж) |
|
|
|
dx |
|
|
|
; з) |
|
|
|
|
|
x |
|
|
dx . |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 x |
|
|
|
x |
|
|
|
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1) |
Вычислить интегралы: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
||||
|
|
2t 2 |
3t 2 dt ; б) |
|
|
|
|
|
|
|
|
cos( x)dx ; г) |
sin2 (x)dx ; |
|||||||||||||||||||||||
а) |
|
|
3 |
xdx ; в) |
||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
4x 3 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
д) |
|
|
|
|
dx ; |
е) |
|
x |
|
1 x |
2 |
dx ; ж) |
x sin(x)dx ; |
|||||||||||||||||||||||
2x 2 3x 4 |
|
|
|
|
||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
з) |
ln(x 1)dx ; и) x arctg( x)dx . |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
Вычислить площадь фигуры, ограниченной линиями: |
|||||||||||||||||||||||||||||||||||
а) y x 2 2x 3, y 0 ; |
б) y x 2 4x, y x 4 0 ; |
|||||||||||||||||||||||||||||||||||
в) y x 2 6x, y 0 ; |
|
г) y 2x2 , x 1, x 2, у 0 ; |
||||||||||||||||||||||||||||||||||
д) |
y 3x 2 |
6x, x 4, ось Ох на отрезке . |
|
|
|
|||||||||||||||||||||||||||||||
4. ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
4.1. Понятие функции двух переменных.
Будем рассматривать две независимые переменные х и у. Каждой паре значений х и у на плоскости соответствует точка, для которой х и у являются координатами. Возьмем на плоскости множество точек и обозначим его D {x, y} .
24
Величина z называется функцией переменных величин х и у на множестве D, если каждой точке этого множества соответствует одно определенное значение величины z. Обозначается функция z f (x, y).
Множество D называется областью определения функции. Графиком функции двух независимых переменных является неко-
торая поверхность в пространстве.
Рассмотрим функцию z f (x, y) . Положим z C , где С – постоянная величина. Тогда уравнение C f (x, y) дает зависимость между
переменными х и у, при которой заданная функция z сохраняет заданное значение C. Геометрически это означает, что поверхность z f (x, y) пересекается плоскостью z C , параллельной плоскости
xOy . В результате такого пересечения полученная линия проектируется на плоскость xOy и задается уравнением C f (x, y) . При перемещении точки с координатами (x; y) вдоль этой линии функция со-
храняет постоянное значение, равное С.
Линия на плоскости xOy , в каждой точке которой функция z f (x, y) сохраняет постоянное значение, называется линией уровня этой функции.
Пример. Найти линии уровня функции z x2 y2 .
Решение. Поверхность, определяемая функцией z x2 y2 , является параболоидом вращения. Линиями уровня являются концентрические окружности x2 y2 C .
4.2. Частные производные
Предположим, что функция z f (x, y) определена в окрестности точки P0 (x0 , y0 ) . Дадим независимой переменной х приращение x . При этом переменная у будет сохранять свое значение. Тогда функция
z f (x, y) получит |
приращение x z f (x0 x, y0 ) f (x0 , y0 ) по |
переменной х в точке |
(x0 ; y0 ) . Это приращение называется частным |
приращением функции по переменной х в точке (x0 ; y0 ) . Аналогично определяется частное приращение функции по переменной у в точке
(x0 ; y0 ) : y z f (x0 , y0 y) f (x0 , y0 ) .
Частной производной функции z f (x, y) называется предел от-
ношения частного приращения функции к частному приращению соответствующего аргумента, если последнее стремится к нулю:
25
z' |
lim |
|
z |
|
z' |
lim |
y z |
|
x |
|
, |
|
. |
||||
|
|
|
||||||
x |
x 0 |
x |
|
y |
y 0 |
y |
||
|
|
|
||||||
По определению частная производная функции двух переменных находится как производная функции одной переменной, когда вторая переменная остается постоянной. Поэтому вычисление частных производных ничем не отличается от вычисления производных функции одной переменной и выполняется по тем же правилам.
Пример 1. Найти частные производные функции двух переменных z 2x3 y 7xy 2 3x 5 .
Решение. Найдем частную производную по переменной х, считая переменную у постоянной: zx' 6x2 y 7 y2 3 . Теперь будем считать, что переменная х остается постоянной: z'y 2x3 14xy .
Предположим, что частные производные zx' и z'y функции z f (x, y) в свою очередь являются функциями независимых переменных х и у. Тогда частные производные от этих частных производ-
ных называются частными производными второго порядка или вторы- |
|||||||||||||
ми |
частными |
производными |
функции z f (x, y) : |
z'' |
z' |
' , |
|||||||
|
z' |
' , |
|
z' |
' , |
|
|
|
|
|
xx |
x |
x |
z'' |
z'' |
z'' |
z' |
' |
. Производные z'' |
и z'' |
называются |
||||||
xy |
x |
y |
yx |
y |
x |
yy |
y |
y |
xy |
yx |
|
|
|
смешанными и они равны между собой.
Пример 2. Найти частные производные второго порядка функции z x3 y 2 3xy 3 xy 1 .
Решение. |
|
|
z ' |
3x 2 y 2 3y3 y , z ' 2x3 y 9xy 2 x , |
||||||||
|
|
|
|
|
|
|
x |
|
|
y |
|
|
z'' |
z' |
' |
|
|
|
3x2 y2 3y3 y ' |
|
6xy 2 , |
|
|
||
xx |
|
x |
x |
|
|
|
x |
|
|
|
|
|
z'' |
z' |
' |
|
|
3x2 y2 3y3 y ' |
|
6x2 y 9y2 1 , |
|||||
xy |
|
x |
|
y |
|
|
|
y |
|
|
|
|
z'' |
z' |
' |
|
|
2x3 y 9xy 2 x ' |
|
6x2 y 9y2 |
1 , |
||||
yx |
|
y |
|
x |
|
|
|
x |
|
|
|
|
z '' |
z ' |
|
' |
|
= 2x3 y 9xy 2 x ' |
|
= 2x3 18xy . |
|
|
|||
yy |
|
y |
|
y |
|
y |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
4.3. Экстремум функции двух переменных |
|||||||
Пусть |
функция z f (x, y) |
|
определена |
в |
некоторой области |
|||||||
D {x, y} |
и пусть точка P0 (x0 ; |
y0 ) D . Точка |
P0 (x0 ; y0 ) называется |
|||||||||
|
|
|
|
|
|
|
|
|
|
26 |
|
|
точкой максимума функции z f (x, y) , если f (x0 , y0 ) есть наибольшее значение функции в окрестности этой точки. Точка P0 (x0 ; y0 ) называется точкой минимума функции z f (x, y) , если f (x0 , y0 )
есть наименьшее значение функции в окрестности этой точки. Точки максимума и минимума называются точками экстремума.
Значение функции в точке максимума называется максимумом функции, а значение функции в точке минимума – минимумом функции. Максимум и минимум функции называются экстремумами функции.
Если в точке P0 (x0 ; y0 ) функция z f (x, y) имеет экстремум, то частные производные функции в этой точке равны нулю, т. е. zx' (x0 , y0 ) 0 и z'y (x0 , y0 ) 0 . Это необходимые условия экстремума.
Точка, в которой обе частные производные равны нулю, называется критической точкой функции z f (x, y) . Для отыскания критиче-
ских точек функции нужно найти ее частные производные, приравнять их нулю и решить систему двух уравнений с двумя неизвестными:
' |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zx |
Точки экстремума, |
если они есть, находятся среди критиче- |
|||||||||||||||
|
|
|
|||||||||||||||
z'y |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ских точек функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть |
|
P0 (x0 ; y0 ) |
является критической точкой |
функции |
|||||||||||||
z f (x, y). |
Вычислим частные производные второго порядка в этой |
||||||||||||||||
точке: |
z'' |
(x , y ) A , |
z'' |
(x , y |
0 |
) B , |
z'' |
(x , y |
0 |
) C . Составим выра- |
|||||||
|
|
xx |
0 |
0 |
xy |
0 |
|
|
yy |
0 |
|
|
|
|
|||
жение AC B2 |
и проанализируем его знак: |
|
|
|
|
|
|||||||||||
1) |
если |
AC B2 0 , |
то |
функция |
z f (x, y) в точке |
P (x ; y ) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
имеет экстремум: максимум при A < 0 и минимум при A > 0;
2)если AC B2 0 , то функция z f (x, y) в точке P0 (x0 ; y0 ) экстремума не имеет;
3)если AC B2 0 , то для определения экстремума нужны дополнительные исследования.
Рассмотренные условия называются достаточными условиями экстремума.
|
Пример. Исследовать функцию |
z 2x3 xy 2 |
5x2 |
y2 |
на экстре- |
|
мум. |
|
|
|
|
|
|
|
Решение. |
Найдем частные |
производные |
z' |
6x2 |
y2 10x , |
|
|
|
|
x |
|
|
z' |
2xy 2 y |
и решим систему уравнений: |
|
|
|
|
y |
|
|
|
|
|
|
|
|
27 |
|
|
|
|
6x2 y2 10x 0,
2xy 2 y 0.
Из второго уравнения 2y(x+1)=0, y=0, x= 1. Подставим у=0 в пер-
вое уравнение: |
6x2 10x 0 , 2x(3x+5)=0, x=0, |
3x+5=0, x |
5 |
. Таким |
|||||
|
|
||||||||
|
|
|
|
|
3 |
|
|||
|
|
|
|
|
5 |
|
|
|
|
образом, найдены две критические точки M1 |
(0; 0) , M 2 |
|
|
|
; 0 . Те- |
||||
|
|
|
|||||||
|
|
|
|
|
3 |
|
|
|
|
перь в |
первое |
уравнение |
подставим x= 1: |
6 y2 10 0 , |
|
y2 4 , |
|||
y 2 , |
y 2 . |
Следовательно, стали известны еще две критические |
|||||||
точки M3 ( 1; 2) , M4 ( 1; 2) . Найдем частные производные второго |
|||||||||
порядка: z'' 12x 10 , z'' |
2 y , z'' 2x 2 . |
|
|
|
|
|
|
||
|
xx |
xy |
yy |
|
|
|
|
|
|
Проверим достаточные условия для точки M1 (0; 0) : |
|
|
|
|
|
||||
A z'' (0,0) 12 0 10 10 , B z'' (0,0) 2 0 0 , |
|
|
|
|
|
||||
|
xx |
|
xy |
|
|
|
|
|
|
Cz'yy' (0,0) 2 0 2 2 , AC B2 10 2 02 10 . Следовательно,
вточке M1(0; 0) функция имеет экстремум. Так как A > 0, то это ми-
нимум. При этом zmin 2 03 0 02 5 02 |
02 |
0 . |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
Аналогично установим, |
что в точке |
|
M 2 |
|
|
; 0 |
функция имеет |
||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 3 |
|
|
5 |
|
|
2 |
|
|
|
|
5 |
2 |
|
2 |
|
17 |
|
||
максимум, причем zmax 2 |
|
|
|
|
|
|
|
|
0 |
|
5 |
|
|
|
|
0 |
|
4 |
|
. В |
|||||
|
|
3 |
|
|
|
27 |
|||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||
точках M3 ( 1; 2) и M4 ( 1; 2) экстремума нет. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
5. ЗАДАНИЯ, РЕКОМЕНДУЕМЫЕ |
|
|
|
|
|
|
|||||||||||||||||
|
|
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ |
|
|
|
|
|
||||||||||||||||||
ПО ТЕМЕ «ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ» |
|
||||||||||||||||||||||||
1) |
Найти частные производные первого и второго порядков функ- |
||||||||||||||||||||||||
ций: |
а) z 3x2 |
4xy 2 5y3 |
2x y 1 ; |
|
|
б) |
z 2x2 y3 |
3x3 y xy ; |
|||||||||||||||||
в) z |
xy |
(x y) sin(x y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
; г) z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2) Исследовать функции на экстремум:
а) |
z xy x2 3y2 x 10y 8 ; б) z 3x2 3xy y2 6x 2y 1 ; |
в) |
z 3xy x2 4y2 4x 6y 1 . |
|
28 |
6.ДВОЙНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
6.1.Двойной интеграл и его свойства
Пусть функция f (x, y) определена в некоторой замкнутой области D плоскости xOy . Разобьем область D произвольным образом на n
частей s1, s2 , , sn с площадями s1, s2 , , sn . Внутри каждой элементарной области si выберем произвольную точку Mi (xi ; yi ) и
найдем значение функции f (xi , yi ) в этой точке. Составим сумму:
In f (M1 ) s1 f (M2 ) s2 f (Mn ) sn
|
n |
n |
|
f (M i ) si f (xi , yi ) si |
|
|
i 1 |
i 1 |
Эта |
сумма называется |
n-й интегральной суммой для функции |
f (x, y) |
по области D. |
|
Диаметром области si |
назовем наибольшее из расстояний между |
|
точками границы этой области и обозначим di .
Если существует конечный предел последовательности интегральных сумм In при стремлении к нулю наибольшего из диаметров ча-
стичных областей si , не зависящий ни от способа разбиения области D , ни от выбора точек Mi , то он называется двойным интегралом от
функции |
f (x, y) |
по области D и обозначается f (x, y)ds . Таким |
||||
|
|
|
|
|
|
D |
|
|
|
|
|
n |
|
образом, |
f (x, y)ds |
lim |
|
f (xi , yi ) si . |
||
|
D |
|
|
maxdi 0 i 1 |
|
|
Если функция |
f (x, |
y) непрерывна в замкнутой области D , то она |
||||
интегрируема по этой области. |
|
|||||
|
|
|
Свойства двойного интеграла |
|||
1. сf (x, y)ds с f (x, y)ds, |
с const. |
|||||
D |
|
|
D |
|
|
|
2. ( f1 (x, y) f2 (x, y))ds f1 (x, y)ds f2 (x, y)ds . |
||||||
D |
|
|
|
|
D |
D |
|
|
|
|
|
|
29 |
3. Если область интегрирования |
D разбить на две области D1 и |
|
D2 без общих внутренних точек, то |
|
|
f (x, y)ds f (x, y)ds f (x, y)ds . |
||
D |
D1 |
D2 |
6.2.Вычисление двойного интеграла
впрямоугольных декартовых координатах
Впрямоугольной системе координат элемент площади ds можно записать в виде произведения dx dy . Тогда
f (x, y)ds = f (x, y)dxdy .
D D
Область D называется правильной в направлении оси Ox (или
Oy ), если любая прямая, проходящая параллельно этой оси, пересека-
ет границу области D не более, чем в двух точках.
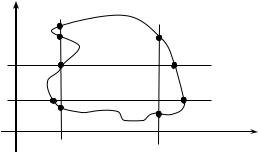
Например, область D на рис. 1 является неправильной в направлении оси Oy и правильной в направлении оси Ox (прямая MN пересе-
кает границу области D в четырех точках).
y
|
N |
|
D |
|
M |
0 |
x |
|
Рис. 1 |
Вычисление двойного интеграла сводится к вычислению повторного интеграла следующим образом.
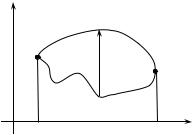
1) Пусть область D является правильной в направлении оси Оу и
ограничена линиями: |
y 1 (x), y 2 (x), x a, y b, |
причем a b, |
1 (x) 2 (x) (рис. 2). |
|
|
|
30 |
|
y |
|
y 2 |
(x) |
|
|
||
|
A |
y |
|
|
|
B |
|
|
|
|
|
|
|
y 1 (x) |
|
0 |
|
a |
b x |
Рис. 2
При выборе внешнего интегрирования по переменной x (из рис. 2 видно a x b ) для определения внутренних пределов интегрирования по переменной y по области интегрирования проводим прямую, параллельную оси Oy снизу вверх. Прямая сначала пресекает кривую
y 1 (x) , которую назовем линией входа. При выходе из области интегрирования прямая пересечет кривую y 2 (x) , которую назовем линией выхода. То есть значение переменной y в области D меняется в пределах 1 x y 2 x .
Тогда |
b |
2 ( x) |
f (x, y)dxdy = dx |
f (x, y)dy . |
|
D |
a |
1 ( x) |
Правая часть формулы называется повторным интегралом.
Таким образом, вычисление двойного интеграла свелось к вычислению повторного (двух определенных интегралов) интеграла вида
b |
2 ( x) |
dx |
f (x, |
a |
1 ( x) |
b 2 |
( x) |
|
|
|
f (x, y)dy |
|
|
y)dy |
dx . |
||
a |
1 |
( x) |
|
При вычислении «внутреннего интеграла» (записанного в квадратных скобках) x считается постоянным.
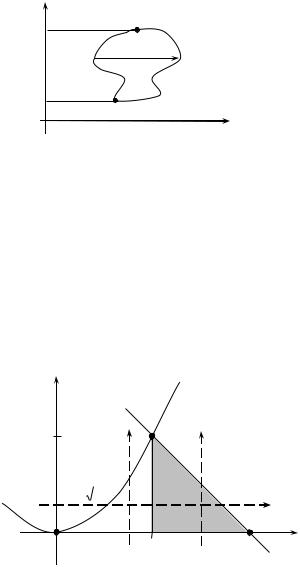
2) Аналогичная формула вычисления двойного интеграла справед-
лива в случае, когда |
D является правильной в направлении оси Ox и |
||
ограничена линиями: |
x 1 ( y), x 2 ( y), y c, y d , причем |
c d, |
|
1 ( y) 2 ( y) (рис. 3). |
|
|
|
|
d |
2 ( y) |
|
Тогда f (x, y)dxdy = dy |
f (x, y)dx . |
|
|
D |
c |
1 ( y) |
|
При вычислении «внутреннего интеграла» y считается постоянным.
31
y
D
d
x 2 ( y)
x
x 1 ( y)
c
C
0 |
x |
Рис. 3
Формулы перехода от двойного интеграла к повторному показывают, что в двойном интеграле можно изменять порядок интегрирования
b |
2 |
x |
d |
2 ( y ) |
dx |
f x, y dy dy |
f ( x, y)dx . |
||
a |
1 |
x |
c |
1 ( y ) |
Если область интегрирования является неправильной, то ее можно представить как объединение правильных областей. Тогда двойной интеграл равен сумме двойных интегралов по этим областям.
Пример 1. В двойном интеграле f x, y dxdy расставить пределы
D
интегрирования двумя способами, если область D ограничена линия-
ми y x2 , |
x y 2 , |
x 0 . |
|
|
||||
Решение. Построим область D (рис. 4). |
|
|||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
B(1; 1) |
|
|
|
|
|
y x 2 |
|
y 2 x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y |
|
x 2 y |
||
|
|
|
|
|
y 0 |
|
y 0 A(2; 0) |
|
|
|
|
O(0; 0) |
1 |
x |
|||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Рис. 4
Найдем точки пересечения линий y x 2 , x y 2 , решая систему уравнений,
32
