Metodichka_chast_2

9. Вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в степенной ряд и почленного интегрирования этого ряда

10. При указанных начальных условиях найти три первых отличных от нуля члена разложения в степенной ряд функции y = f(x), являющейся решением заданного дифференциального уравнения

64

10.ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

10.1.Задачи математической статистики

Математическая статистика – это один из разделов математики. Все основные методы, используемые в математической статистике, основаны на понятиях теории вероятностей.

Каждое исследование случайных явлений, выполненное методами теории вероятностей, опирается на экспериментальные данные.

Математическая статистика занимается разработкой методов сбора, описания и анализа экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений.

В любом процессе, связанном с применением статистических методов, можно выделить три этапа: сбор данных, обработка данных, статистические выводы – прогнозы и решения.

Типичными задачами математической статистики являются:

1)определение закона распределения случайной величины по статистическим данным;

2)проверка правдоподобия гипотез;

3)нахождение неизвестных параметров распределения.

Генеральная совокупность. Выборка

Множество однородных объектов, подлежащих статистическому

изучении, называется статистической совокупностью. Отдельные объекты называются элементами совокупности, а их число – объемом совокупности.

Элементы совокупности можно охарактеризовать одним или несколькими признаками, значения которых изменяются при переходе от одного элемента совокупности к другому.

Для изучения вариации (изменения) признака проводится статистическое наблюдение. Различают два вида статистических наблюде-

ний: сплошное и выборочное.

При сплошном наблюдении изучается каждый элемент совокупности. Однако такое наблюдение сопряжено со значительными затратами труда или же может оказаться вообще неосуществимым.

По этой причине в большинстве случаев используют выборочное наблюдение, в основе которого лежит выделение из статистической совокупности некоторой ее части – выборочной совокупности (выборки). Исходная совокупность в этом случае называется генеральной со-

вокупностью.

Главная задача выборочного метода заключается в том, чтобы по статистическим показателям малой выборки как можно точнее охарактеризовать всю генеральную совокупность. Другими словами, при помощи сравнительно ограниченных средств, которые дают возможность

65

изучать единичные явления, установить характерные свойства и законы для бесконечного числа возможных или встречающихся явлений.

Таким образом, основополагающая задача математической ста-

тистики заключается в исследовании свойств выборки и обобщении этих свойств на всю генеральную совокупность.

Статистический закон распределения.

Пусть для изучения некоторой случайной величины Х из генеральной совокупности извлечена выборка x1, x2 ,...,xn объема n. Предста-

вим значения выборки в виде таблицы, в первой строке которой даны номера элементов выборки, а во второй – сами элементы. Такая табли-

ца называется простым статистическим рядом.

Статистические данные в виде простого статистического ряда при большом объеме выборки довольно трудно обработать. В этом случае производят группировку данных.

При изучении дискретной случайной величины наблюденные значения располагаются в порядке возрастания, а затем подсчитываются частоты mi , т.е. количество появлений одинаковых значений случай-

Если изучается непрерывная случайная величина, то для выполнения группировки нужно весь интервал наблюденных значений случайной величины разбить на k частичных интервалов равной длины. Затем

наблюденных значений в частичные интервалы. Количество k интервалов выбирается произвольно в пределах от 5 до 15, но рекомендуется определять k по формуле k 1 3,2lgn , где n – объем выборки. Ре-

66

зультаты записываются в виде таблиц:

Интервальный статистический ряд распределения частот

Перечень наблюденных значений xi случайной величины Х (или интервалов наблюденных значений) и соответствующих им относи-

Построить статистический ряд распределения относительных частот.

Решение. Выполним группировку и получим статистический ряд распределения частот.

Найдем относительные частоты и результаты запишем в виде статистического ряда распределения относительных частот:

10.2. Эмпирическая функция распределения

67

Эмпирической функцией распределения случайной величины Х называется функция F * (x) , определяющая для каждого значения х

значений xi , меньших, чем х, а n – объем выборки.

Эмпирическая функция распределения обладает всеми свойствами

интегральной функции распределения:

1)значения эмпирической функции принадлежат отрезку [0; 1] ;

2) функция F * (x) – неубывающая;

3)если x1 – наименьшее значение в выборке, а xk – наиболь-

шее, то F* (x) 0 при x x1 и F * (x) 1 при x xk . Пример 1. Построить эмпирическую функцию распределения по

статистическому распределению случайной величины Х:

Графическое изображение статистических рядов

Сгруппированные статистические ряды для наглядности можно представлять графиками и диаграммами. Наиболее распространен-

ными графиками являются полигон, гистограмма и кумулята.

Полигон и кумулята применяются как для дискретных, так и для интервальных статистических рядов. Гистограмма применяется для изображения только интервальных рядов.

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы наблюденных значений случайной величины Х, на каждом из которых строится прямоугольник. Высота прямоугольника равна wi – относительной частоте для

i-го интервала.

Если на гистограмме относительных частот соединить середины верхних сторон элементарных прямоугольников, то полученная замкнутая ломаная линия образует полигон относительных частот.

68

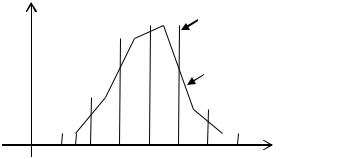
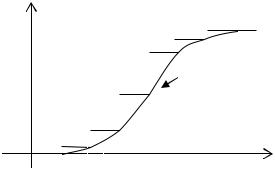
Для построения кумуляты на оси абсцисс откладываются наблюденные значения случайной величины Х, а на оси ординат – накопленные относительные частоты. Значения накопленных относительных частот являются значениями эмпирической функции распределения

F * (x) .

Пример 2. Дано распределение 100 рабочих по затратам времени на обработку одной детали (мин.):

Построить гистограмму, полигон и кумуляту относительных частот по данному распределению.

Решение. Вначале вычислим относительные частоты и запишем статистическое распределение в виде таблицы:

Найдем эмпирическую функцию распределения и построим кумуляту:

69

ч

10.3. Статистические оценки параметров распределения

Статистические распределения содержат полную информацию о вариации признака. Между тем при решении многих задач эта информация может оказаться избыточной.

Для описания статистических распределений обычно используют три вида характеристик (показателей):

1)средние;

2)характеристики изменчивости (рассеяние);

3)характеристики, отражающие дополнительные особенности распределений (в частности их форму).

Все эти характеристики вычисляются по результатам наблюдений и построенных в результате их первичной обработки распределений и называются статистическими. Расчет статистических характеристик является вторым после группировки этапом обработки данных.

Пусть x1, x2 ,...,xn – выборка из генеральной совокупности.

Средним значением выборки или выборочным средним называет-

ся число

70

xв 1 n xi .

n i 1

Эта формула применяется к статистическому ряду, данные которого не сгруппированы. Если же данные сгруппированы, то выборочная средняя (взвешенная средняя арифметическая) вычисляется по фор-

мулам

стоты и относительные частоты в этих формулах называются весами. Пример 1. В сельхозпредприятии собран урожай пшеницы с трех

различных участков. С первого участка площадью в 240 га получено по 30 ц/га, со второго на площади 260 га – по 28 ц/га и с третьего площадью 500 га – по 34 ц/га. Определить среднюю урожайность.

Решение. Запишем данные урожая пшеницы в виде таблицы:

Чем теснее отдельные значения признака группируются вокруг средней, т.е. чем меньше они рассеяны, тем лучше выборочная средняя характеризует данное распределение. Поэтому кроме выборочной средней нужно рассматривать вариацию признака относительно средней, т.е. характеристики рассеяния. В практике, как правило, оценка рассеяния является не менее важной, чем выборочная средняя.

Наиболее грубая оценка рассеяния легко определяется по данным статистического ряда и называется размахом выборки:

R xmax xmin .

Однако этот показатель может сильно меняться при добавлении или исключении крайних значений. Поэтому, если данные не сгруппированы, то в качестве меры рассеяния используется выборочная дисперсия, определяемая по формуле

n

Dв 1 (xi xв )2 . n i 1

Если же данные сгруппированы, то для определения выборочной дисперсии используются формулы

71

В практических вычислениях для определения дисперсии удобнее пользоваться формулой

Dв x2 xв 2 ,

n

где x2 1 xi 2 для данных, которые не сгруппированы; n i 1

k

x2 1 xi 2mi для данных, которые сгруппированы.

n i 1

Так как при вычислении дисперсии суммируются квадраты отклонений, то дисперсия измеряется в квадратных единицах. Вследствие этого получается искаженное представление о самой величине отклонений и о величине значений признака. Чтобы согласовать единицы измерения рассеяния и значений признака, вводится среднее квадра-

тическое отклонение

в Dв ,

которое показывает, на сколько в среднем отклоняются значения xi признака от выборочной средней xв .

Коэффициент вариации вычисляется по формуле

V в 100% xв

и применяется для оценки вариации в распределениях с разными значениями средней.

Кроме рассмотренных характеристик в статистическом анализе применяются медиана и мода.

Медиана Me( X ) – это значение признака X, разделяющее ранжированную совокупность на две равные по численности группы. В первой группе содержатся элементы со значениями признака xi Me(X ) , а во второй – со значениями признака xi Me(X ) . Из определения

накопленной относительной частоты следует, что F* (Me(X )) 0,5 . Для определения медианы Me( X ) интервального ряда пользуются

формулой

Me( X ) x0 h n 2 n1 ,

2 mMe

72