
- •Введение
- •Тема 1. Элементы векторной алгебры
- •Решение типового примера
- •Тема 2. Элементы аналитической геометрии на плоскости и в пространстве
- •Решение типового примера
- •Решение типового примера
- •Тема 3. Введение в мАтематический анализ функции одной переменной
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Тема 4. Дифференциальное исчисление функции одной переменной и его применение к исследованию функции
- •Вопросы программы для изучения и самопроверки
- •Решение типовых примеров
- •Правила дифференцирования
- •Решение типового примера
- •Тема 5. ФункциИ двух независимых переменных
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Решение типового примера
- •Тема 6. Неопределенный интеграл
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Основная таблица интегралов
- •Тема 7. Определенный интеграл и его применение для вычисления площадей плоских фигур
- •Вопросы для изучения и самопроверки
- •Решение типового примера
- •Решение типового примера
- •Тема 8. Дифференциальные уравнения первого порядка
- •Вопросы для изучения и самопроверки
- •Решение типового примера
- •Решение типового примера
- •Тема 9. Основные понятия и задачи теории
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Решение типового примера
- •Решение типового примера
- •Решение типового примера
- •Решение типового примера
Решение типовых примеров
П р и м е р ы. Найти частные производные 1-го порядка заданных функций..
1.
![]() .
.
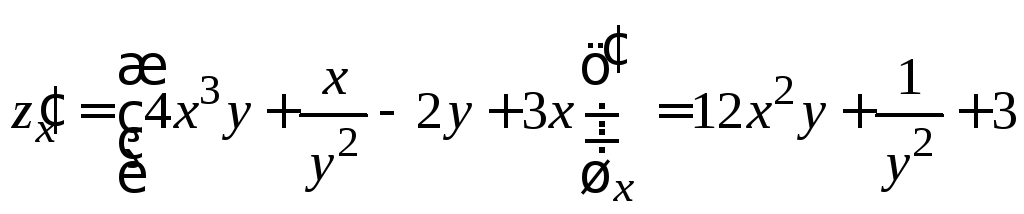 .
.
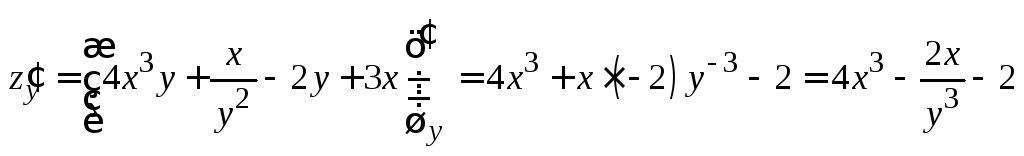 .
.
2.
![]() .
.
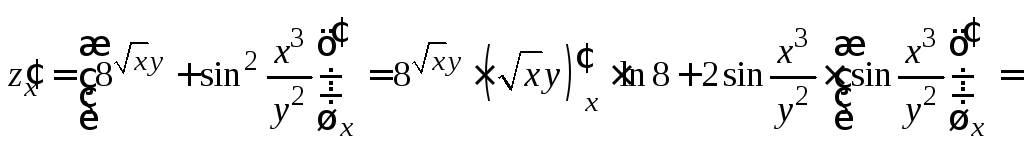
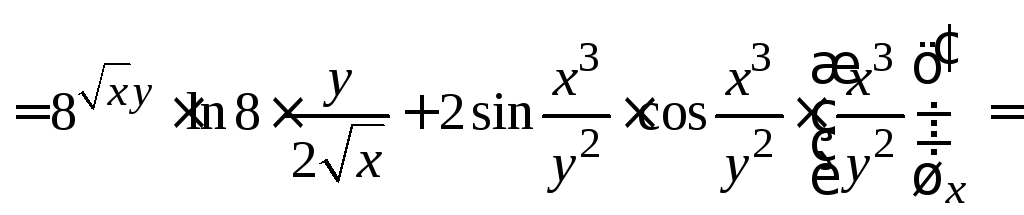
![]() ;
;
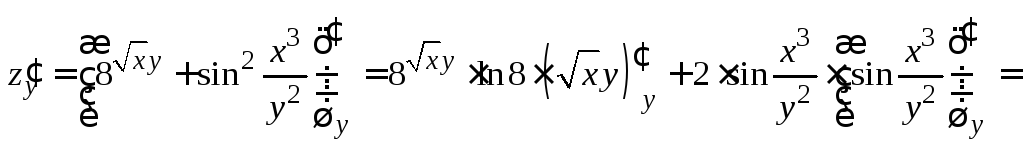

![]() .
.
Задачи 141–160. Исследовать на экстремум заданные функции.
141.
![]() .
.
142.
![]() .
.
143.
![]() .
.
144.
![]() .
.
145.
![]() .
.
146.
![]() .
.
147.
![]() .
.
148.
![]() .
.
149.
![]() .
.
150.
![]() .
.
151.
![]() .
.
152.
![]() .
.
153.
![]() .
.
154.
![]() .
.
155.
![]() .
.
156.
![]() .
.
157.
![]() .
.
158.
![]() .
.
159.
![]() .
.
160.
![]() .
.
Решение типового примера
Найти
экстремум функции
![]() ,
если
,
если![]() .
.
Р е ш е н и е.
1.
Областью определения функции являются
все точки координатной плоскости
![]() .
.
2. Находим частные производные первого порядка:
![]() ;
;
![]() .
.
Приравняем частные производные к нулю, решив полученную систему, получим критическую точку
![]()
Точка
![]() –
стационарная, подозрительная на
экстремум.
–
стационарная, подозрительная на
экстремум.
3. Находим частные производные второго порядка:
![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
Таким образом получаем
![]() ;
;
![]() ;
;![]() .
.
Составим
выражение
![]() .
.
Так
как
![]() следовательно точка
следовательно точка![]() не является точкой экстремума.
не является точкой экстремума.
Тема 6. Неопределенный интеграл
Для решения задач по этой теме нужно обратить внимание на определения первообразной и неопределенного интеграла, свойства неопределенного интеграла, усвоить таблицу основных интегралов и основные методы интегрирования. Успех в решении задач достигается правильным выбором метода интегрирования и накопленным опытом вычисления интегралов. Особое внимание уделить методам подстановки и интегрирования по частям. При вычислении интегралов от рациональных дробей нужно усвоить методику разложения рациональных дробей на простейшие дроби и их интегрирование.
Вопросы для изучения и самопроверки
1. Понятие первообразной.
2. Неопределенный интеграл и его свойства.
3. Таблица интегралов.
4. Основные методы интегрирования.
5. Рациональные дроби, разложение на простейшие дроби.
6. Интегрирование простейших дробей.
7. Интегрирование рациональных дробей.
Задачи 161–180. Найти неопределенные интегралы и результаты проверить дифференцированием.
161.
а)![]() б)
б)![]() ;
;
в)![]() .
.
162.
а)![]() ;
б)
;
б)![]() ;
;
в)![]() .
.
163.
а)![]() б)
б)![]()
в)![]()
164.
а)![]() б)
б)![]()
в)![]()
165.
а)![]() б)
б)![]()
в)![]()
166.
а)![]() б)
б)![]()
в)![]()
167.
а)![]() б)
б)![]()
в)![]()
168.
а)![]() б)
б)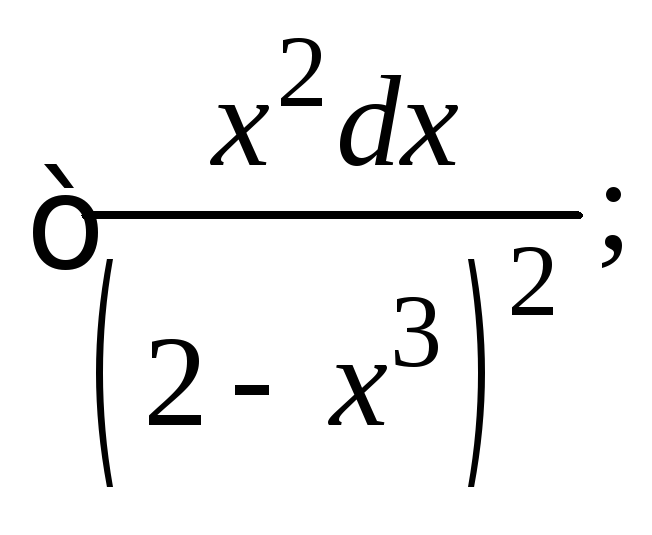
в)![]()
169.
а)![]() б)
б)![]()
в)![]()
170.
а)![]() б)
б)![]()
в)![]()
171.
а)![]() б)
б)![]()
в)![]()
172.
а)![]() б)
б)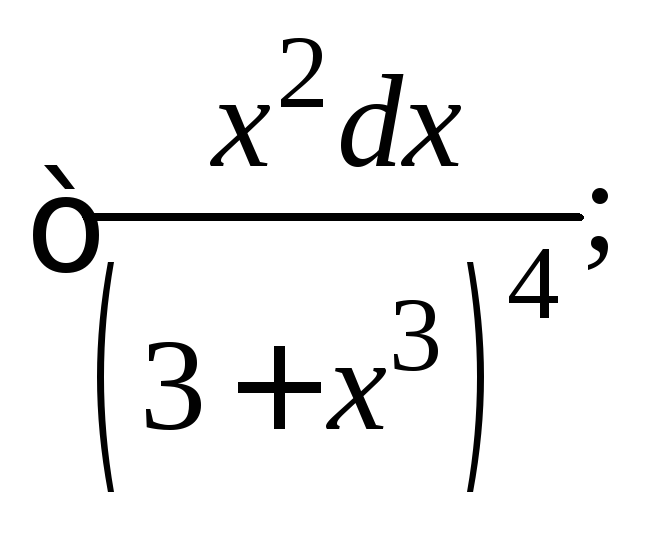
в)![]()
173.
а)![]() б)
б)![]()
в)![]()
174.
а)![]() б)
б)![]()
в)
![]()
175.
а)![]() б)
б)![]()
в)![]()
176.
а)![]() б)
б)![]()
в)![]() .
.
177.
а)![]() б)
б)![]()
в)![]()
178.
а)![]() б)
б)![]()
в)![]()
179.
а)![]() б)
б)![]()
в)
![]()
180.
а)![]() б)
б)![]()
![]()
в)![]()
Решение типовых примеров
При решении примеров рекомендуется использовать свойства неопределенного интеграла, таблицу интегралов, применять методы замены переменной и интегрирования по частям в неопределенном интеграле.
Основная таблица интегралов
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]()
П р и м е р ы. Найти неопределенные интегралы и результаты проверить дифференцированием.
![]()
=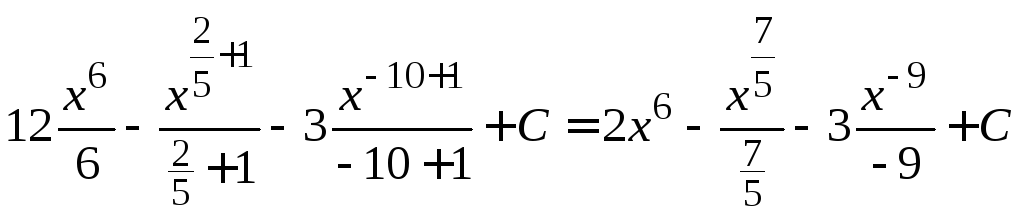 =
=
=![]()
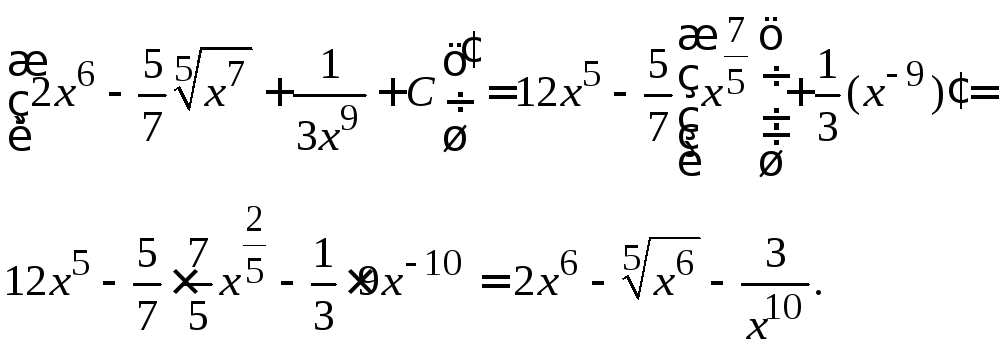
При
решении примера использовались свойства
степени:
![]()
2.
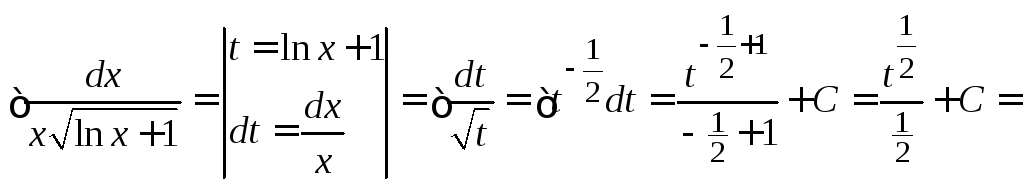
=![]()
При решении примера применялся метод замены переменной.
![]() .
.
3.

=![]()
При решении примера применялся метод интегрирования по частям.
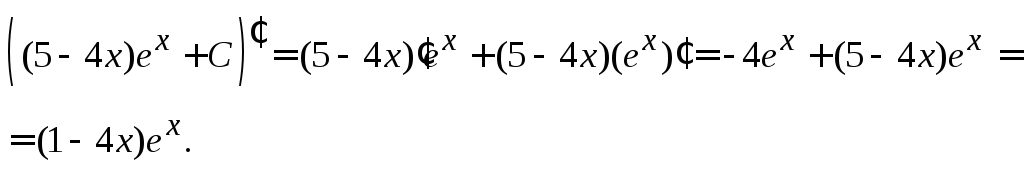
Тема 7. Определенный интеграл и его применение для вычисления площадей плоских фигур
Изучение темы следует начинать с задач, приводящих к понятию определенного интеграла. Усвоить определение и свойства определенного интеграла, формулу Ньютона–Лейбница и ее применение. Изучить методы вычисления определенного интеграла и их специфику по сравнению с аналогичными методами в неопределенном интеграле, обратить внимание на применение определенного интеграла в геометрии и при решении конкретных практических задач.
