Решение типовых примеров

П р и м е р ы. Найти указанные пределы:

1. .

2. .

При подстановке предельного значения х=-1 получим неопределенность вида . Для раскрытия неопределенности в данном случае разложим числитель и знаменатель дроби на линейные множители по формуле:, где х₁ и х₂ –корни квадратного трехчлена .

.

.

Следовательно:

.

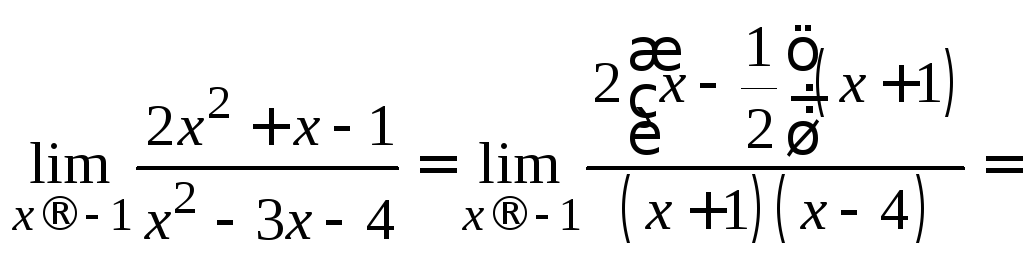
3. Для раскрытия неопределенности

разделим числитель и знаменатель дроби на переменную в старшей степени, т.е. на х²:

.

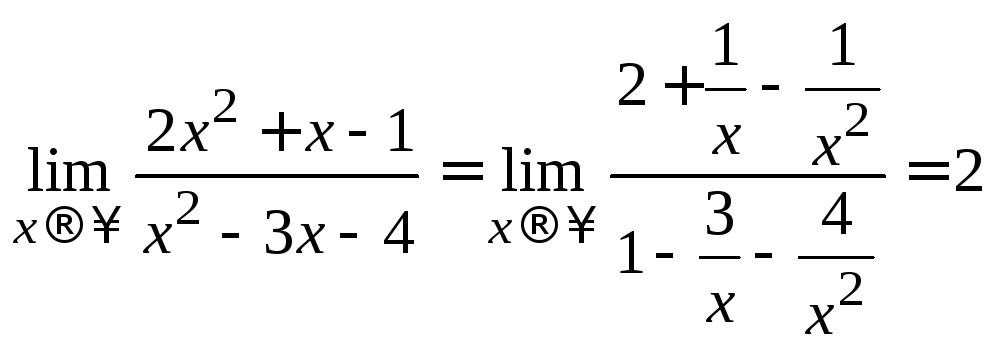4. . В данном случае неопределенность видараскрываем с использованием первого замечательного предела и его следствия:;.

.

5. . Для раскрытия данного вида неопределенности нужно домножить числитель и знаменатель дроби на выражение, сопряженное числителю:

=

.

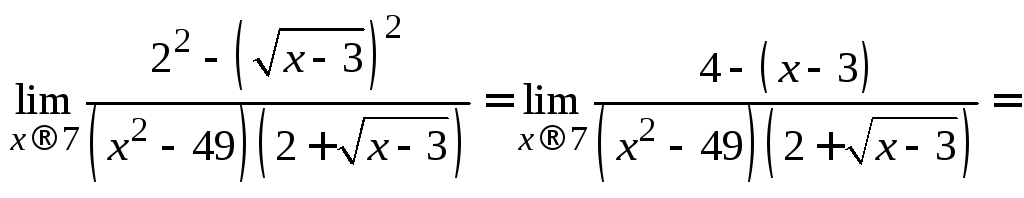
Необходимо знать формулу: .

Тема 4. Дифференциальное исчисление функции одной переменной и его применение к исследованию функции

Изучение этой темы следует начать с разбора решений задач, приводящих к понятию производной. Это позволит осмыслить и понять определение производной, условия ее существования, ее геометрический и механический смыслы. Особое внимание необходимо обратить на теоремы и правила, позволяющие упростить вычисление производных. Успешное применение производной при решении задач зависит от усвоения понятий возрастания и убывания функций, наибольших и наименьших значений функции, экстремумов функции, выпуклости и вогнутости кривой.

Вопросы программы для изучения и самопроверки

1. Производная функции, ее геометрический смысл.

2. Правила дифференцирования функций.

3. Производная сложной, неявно заданной и обратной функций.

4. Дифференцирование функций, заданных параметрически.

5. Дифференциал функции.

6. Производные и дифференциалы высших порядков.

7. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.

8. Условия возрастания и убывания функций. Экстремум функции. Необходимое условие экстремума. Достаточные признаки существо- вания экстремума.

9. Наибольшее и наименьшее значения непрерывной на отрезке функции.

10. Выпуклость и вогнутость графика функции. Точки перегиба.

11. Асимптоты кривых.

Задачи 81–100. Найти производные заданных функций.

81. а) ;	б) ;
в) .
82. а) ;	б) ;
в) .
83. а) ;	б) ;
в) .
84. а) ;	б) ;
в) .
85. а) ;	б) ;
в) .
86. а) ;	б) ;
в) .
87. а);	б) ;
в) .
88. а) ;	б) ;
в) .
89. а) ;	б) ;
в) .
90. а) ;	б) ;
в) .
91. а) ;	б) ;
в) .
92. а) ;	б) ;
в) .
93. а) ;	б) ;
в) .
94. а) ;	б) ;
в) .
95. а) ;	б) ;
в) .
96. а) ;	б) ;
в) .
97. а) ;	б) ;
в) .
98. а) ;	б) ;
в) .
99. а) ;	б) ;
в) .
100. а) ;	б) ;
в) .