
- •Введение
- •Тема 1. Элементы векторной алгебры
- •Решение типового примера
- •Тема 2. Элементы аналитической геометрии на плоскости и в пространстве
- •Решение типового примера
- •Решение типового примера
- •Тема 3. Введение в мАтематический анализ функции одной переменной
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Тема 4. Дифференциальное исчисление функции одной переменной и его применение к исследованию функции
- •Вопросы программы для изучения и самопроверки
- •Решение типовых примеров
- •Правила дифференцирования
- •Решение типового примера
- •Тема 5. ФункциИ двух независимых переменных
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Решение типового примера
- •Тема 6. Неопределенный интеграл
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Основная таблица интегралов
- •Тема 7. Определенный интеграл и его применение для вычисления площадей плоских фигур
- •Вопросы для изучения и самопроверки
- •Решение типового примера
- •Решение типового примера
- •Тема 8. Дифференциальные уравнения первого порядка
- •Вопросы для изучения и самопроверки
- •Решение типового примера
- •Решение типового примера
- •Тема 9. Основные понятия и задачи теории
- •Вопросы для изучения и самопроверки
- •Решение типовых примеров
- •Решение типового примера
- •Решение типового примера
- •Решение типового примера
- •Решение типового примера
Вопросы для изучения и самопроверки
1. Задачи, приводящие к понятию определенного интеграла.
2. Определенный интеграл и его свойства.
3. Формула Ньютона–Лейбница.
4. Методы вычисления определенного интеграла.
5. Применение определенного интеграла для вычисления площадей и объемов.
6. Применение определенного интеграла в задачах практического характера.
Задачи 181–200. Вычислить определенные интегралы.
181.
а)![]() б)
б) в)
в)![]()
182.
а)![]() б)
б)![]() в)
в)![]()
183.
а)![]() б)
б)![]() в)
в)![]()
184.
а)![]() б)
б)![]() в)
в)
185.
а)![]() б)
б)![]() в)
в)
186.
а)![]() б)
б)![]() в)
в)![]()
187.
а)![]() б)
б)![]() в)
в)![]()
188.
а)![]() б)
б)![]() в)
в)![]()
189.
а)![]() б)
б)![]() в)
в)
190.
а)
![]() б)
б)![]() в)
в)![]()
191.
а)![]() б)
б)![]() в)
в)![]()
192.
а)![]() б)
б)![]() в)
в)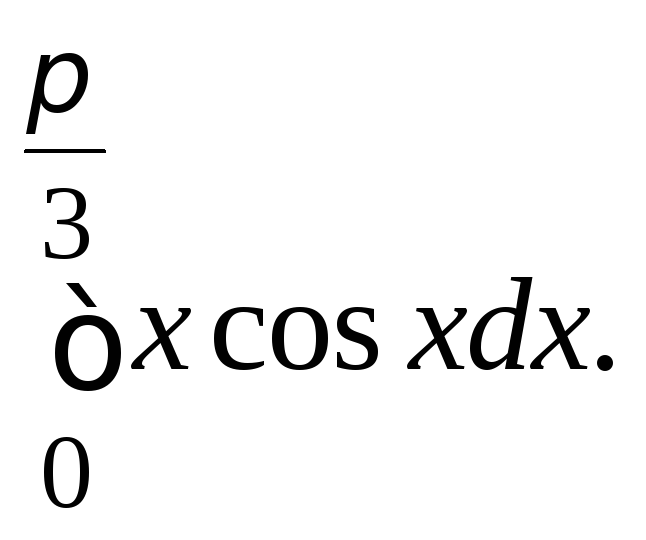
193.
а)![]() б)
б)![]() в)
в)![]()
194.
а)![]() б)
б)![]() в)
в)![]()
195.
а)![]() б)
б)![]() в)
в)![]()
196.
а)![]() б)
б)![]() в)
в)![]()
197.
а)![]() б)
б)![]() в)
в)![]()
198.
а)![]() б)
б)![]() в)
в)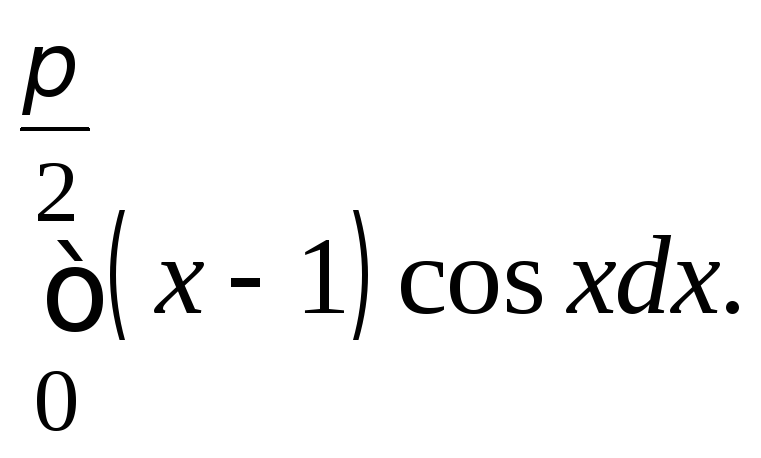
199.
а)![]() б)
б)![]() в)
в)![]()
200.
а)![]() б)
б)![]() в)
в)
Решение типового примера
При решении примеров рекомендуется использовать свойства определенного интеграла, методы замены переменной и интегрирования по частям в определенном интеграле, а также формулу Ньютона–Лейбница:
![]() ,
где
,
где
![]() –первообразная
для
–первообразная
для![]() .
.
П
р и м е р ы. Вычислить определенные
интегралы.
1.![]()
![]()
![]()
![]()
![]()
![]()
=![]()
2.
 =
=![]()
=![]()
При решении примера применялся метод замены переменной в определенном интеграле.
3.![]()

=![]()
При решении примера применялась формула интегрирования по частям в определенном интеграле.
Задачи 201–220. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж и заштриховать искомую площадь.
201.
![]()
202.
![]()
203.
![]()
204.
![]()
205.
![]()
206.
![]()
207.
![]()
208.
![]()
209.
![]()
210.
![]()
211.
![]()
212.
![]()
213.
![]()
214.
![]()
215.
![]()
216.
![]()
217.
![]()
218.
![]()
219.
![]()
220.
![]()
Решение типового примера
П р и м е р. Вычислить
площадь фигуры, ограниченную линиями:
![]()
Р
е ш е н и е.
Построим
линии и заштрихуем искомую площадь. Для
построения параболы
![]() необходимо:
необходимо:
1)
найти точки пересечения линии с осью
ОХ, решив уравнение
![]() ,
,![]() –точки
пересечения линии с осью ОХ;
–точки
пересечения линии с осью ОХ;
2)
найти вершину параболы
![]() тогда
тогда![]() ,
точка
,
точка![]() –
вершина параболы.
–
вершина параболы.
3)
найти точку пересечения с осью ОУ:
![]() тогда
тогда![]()
Строим
параболу, учитывая что ветви линии
направлены вниз. Проводим прямую
![]() и заштриховываем искомую площадь
(рис.2).
и заштриховываем искомую площадь
(рис.2).

Рис. 2.
Решая
уравнение
![]() ,
находим пределы интегрирования
,
находим пределы интегрирования![]() .
.
Вычисляем
искомую площадь по формуле
![]() ,
где
,
где![]() .
.
![]()
![]()
=
![]()
Тема 8. Дифференциальные уравнения первого порядка
Обратить внимание на методы решения дифференциальных уравнений первого порядка:
1) с разделяющимися переменными;
2) однородные;
3) линейные.
Усвоить методику нахождения общего и частного решений.
Изучить методы решения линейных однородных и неоднородных дифференциальных уравнений второго порядка со специальной правой частью.
Вопросы для изучения и самопроверки
1. Задачи, приводящие к дифференциальным уравнениям.
2. Основные понятия теории дифференциальных уравнений.
3. Задача Коши.
4. Дифференциальные уравнения первого порядка: с разделяющи- мися переменными, однородные, линейные.
5. Дифференциальные уравнения второго порядка.
6. Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
7. Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.
Задача 221–240. Найти частное решение дифференциального уравнения с разделяющимися переменными, удовлетворяющее заданному начальному условию.
221.
![]() .
.
222.
![]() .
.
223.
![]() .
.
224.
![]() .
.
225.
![]() .
.
226.
![]() .
.
227.
![]() .
.
228.
![]() .
.
229.
![]() .
.
230.
![]() .
.
231.
![]() .
.
232.
![]() .
.
233.
![]() .
.
234.
![]() .
.
235.
![]() .
.
236.
![]() .
.
237.
![]() .
.
238.
![]()
239.
![]() .
.
240.
![]() .
.
