
- •2.5. Замкнуті системи масового обслуговування 5
- •Таблиця 2.6.Операційні характеристики смо
- •2.6. Смо із взаємодопомогою між каналами
- •2.2. Система масового обслуговування з довільним розподілом часу обслуговування
- •3.1. Критерії оптимізації смо
- •3.2. Оптимізація замкнутої смо за критерієм максимуму прибутку
- •3.3. Оптимізація смо за критерієм мінімуму економічних втрат від відмов в обслуговуванні
- •Контрольні запитання
3.1. Критерії оптимізації смо
Критерієм оптимізації може бути функція, яка виражає прибуток або витрати, пов’язані з простоєм каналів обслуговування і чеканням клієнтів у черзі, або більш точно, математичне сподівання прибутку і витрат, викликаних простоєм каналів обслуговування і чеканням клієнтів. Вартісні оцінки процесу обслуговування у СМО, які повинні бути відображені у критерії оптимальності, складається із таких елементів:
• вхідний потік заявок на обслуговування:
• накопичувач заявок, які чекають обслуговування;
• канали обслуговування;
• вихідний потік обслужених заявок.
Витрати СМО складаються з постійної і змінної складової. Перша складова практично не залежить від того, як організований процес обслуговування заявок і, як правило, включає витрати на придбання і установку устаткування (каналів обслуговування СМО). Друга складова пропорційна кількості обслужених заявок і може суттєво залежати від організації процесу обслуговування. Доходи СМО складаються із доходу за обслуговування заявок і у більшості випадків раціональна організація процесу обслуговування може суттєво їх підвищити. СМО повинна так організувати процес обслуговування, щоб максимізувати одержуваний прибуток, який є різницею між доходами і витратами СМО.
Основними параметрами СМО, на які можна впливати, щоб збільшити прибуток є:
1. Інтенсивність вхідного потоку. Інтенсивність вхідного потоку заявок при раціональній організації процесу обслуговування у СМО (при раціональному співвідношенні з інтенсивністю обслуговування) збільшує прибуток за рахунок зменшення простою каналів обслуговування.
2. Об’єм накопичувача заявок. Збільшення об’єму накопичувача збільшує витрати СМО на його організацію і утримання, але одночасно збільшує доход, оскільки при цьому зменшується частка заявок, які одержують відмову у обслуговуванні у наслідок відсутності вільних місць у накопичувачі.
3. Дисципліна черги, тобто правило вибору заявок на обслуговування. Якщо з точки зору доходу і витрат СМО усі заявки однакові, то дисципліна їх обслуговування для СМО значення не має. Але якщо передбачена платня за терміновість обслуговування, за обслуговування без черги, або якщо знаходження у черзі одних заявок збільшує витрати СМО більше, ніж інших, то вибір дисципліни обслуговування може сильно впливати на прибуток.
4. Час обслуговування заявки і кількість каналів обслуговування (інтенсивність обслуговування). Дані параметри суттєво впливають на характеристики системи обслуговування, а отже, на витрати і доходи СМО.
Розглянуті параметри системи обслуговування можуть розглядатись у якості управляючих і оптимізаційну задачу можна сформулювати так: вибрати параметри СМО, що управляються, таким чином, щоб її доход був максимальний.
3.2. Оптимізація замкнутої смо за критерієм максимуму прибутку
Критерій максимуму валового прибутку при оптимізації СМО враховує прибуток від роботи СМО, прибуток від роботи засобів виробництва при виконанні роботи за їх призначенням і економічні втрати від простою каналів обслуговування та простою засобів виробництва у наслідок перебування їх у неробочому стані.
Прибуток від роботи каналів обслуговування визначається кількістю обслужених заявок і вартістю виконаної роботи за обслуговування заявки, які мають конкретне вартісне вираження і оцінюються безпосередньо. Втрати від простою обслуговуючих каналів і заявок іноді не мають чіткого вартісного вираження і можуть визначатись не прямим шляхом. Наприклад, втрати від затримки обслуговування заявок можуть проявлятись різним чином: штрафи або пені за затримку подальшої роботи заявок, додаткові поточні витрати, втрати якості продукції, зменшення обсягу продукції, що виробляється, втрата очікуваного прибутку тощо. Простої каналів обслуговування викликають втрати прибутку від результатів їх безпосередньої роботи, штраф за їх простоювання, здорожання обслуговування, тощо.
Розглянемо СМО з m каналами обслуговування
і обмеженим джерелом заявок, максимальна
кількість яких не перевищує n (за
класифікацією СМО це є замкнута СМО).
Інтенсивність потоку заявок на
обслуговування від одного джерела
дорівнює
 одиниць, інтенсивність обслуговування
одиниць, інтенсивність обслуговування одиниць (середній час обслуговування
одиниць (середній час обслуговування одиниць часу. Якщо у якості критерію
оптимальності системи прийняти прибуток,
який є різницею між доходом від роботи
заявок і обслуговуючих приладів СМО та
витратами від простою заявок у черзі
на обслуговування або простою каналів
обслуговування, то у загальному випадку
цей критерій буде функцією параметрів
одиниць часу. Якщо у якості критерію
оптимальності системи прийняти прибуток,
який є різницею між доходом від роботи
заявок і обслуговуючих приладів СМО та
витратами від простою заявок у черзі
на обслуговування або простою каналів
обслуговування, то у загальному випадку
цей критерій буде функцією параметрів Зазвичай ставиться частинна задача:
при заданих трьох параметрах визначити
четвертий при умові, що критерій
оптимальності прийме максимальне
значення.
Зазвичай ставиться частинна задача:
при заданих трьох параметрах визначити
четвертий при умові, що критерій
оптимальності прийме максимальне
значення.
Для ілюстрації алгоритму розв'язання
класу задач оптимізації СМО за критерієм
прибутку знайдемо при заданих значеннях
параметрів
 оптимальну
кількість операторів
оптимальну
кількість операторів ,
які обслуговують
,
які обслуговують приладів в одиницю часу. З урахуванням
доходу від роботи каналів обслуговування
і роботи, яку виконують заявки, коли
вини знаходяться у робочому стані, тобто
знаходять поза системою обслуговування,
і загальних витрат від непродуктивних
простоїв і каналів обслуговування і
заявок у черзі, критерій максимуму
валового прибутку у загальному вигляді
може бути таким:
приладів в одиницю часу. З урахуванням
доходу від роботи каналів обслуговування
і роботи, яку виконують заявки, коли
вини знаходяться у робочому стані, тобто
знаходять поза системою обслуговування,
і загальних витрат від непродуктивних
простоїв і каналів обслуговування і
заявок у черзі, критерій максимуму
валового прибутку у загальному вигляді
може бути таким:
 (3.1)
(3.1)
де
 кількість
обслужених заявок, яка також дорівнює
кількості зайнятих каналів обслуговування,
тобто
кількість
обслужених заявок, яка також дорівнює
кількості зайнятих каналів обслуговування,
тобто
 середня кількість незайнятих
каналів обслуговування;
середня кількість незайнятих
каналів обслуговування;
 кількість заявок поза системою
обслуговування (кількість працюючих
засобів виробництва тобто потенційних
заявок на обслуговування у СМО);
кількість заявок поза системою
обслуговування (кількість працюючих
засобів виробництва тобто потенційних
заявок на обслуговування у СМО);
 середня
кількість заявок у черзі;
середня
кількість заявок у черзі;
 економічні
втрати від простою каналів обслуговування,
які приходяться на 1 канал в одиницю
часу;
економічні
втрати від простою каналів обслуговування,
які приходяться на 1 канал в одиницю
часу;
 економічні
втрати, пов’язані з одиницею часу,
проведеному засобом виробництва у
неробочому стані (це час чекання заявки
у черзі на обслуговування плюс час
обслуговування);
економічні
втрати, пов’язані з одиницею часу,
проведеному засобом виробництва у
неробочому стані (це час чекання заявки
у черзі на обслуговування плюс час
обслуговування);
 прибуток
від обслуговування однієї заявки;
прибуток
від обслуговування однієї заявки;
 прибуток,
який приносить засіб ви рибництва у
робочому стані (який є потенційною
заявкою на обслуговування у СМО).
прибуток,
який приносить засіб ви рибництва у
робочому стані (який є потенційною
заявкою на обслуговування у СМО).
Алгоритм розв’язання задачі оптимізації
у даній постановці зводиться до обчислення
ймовірностей станів СМО, визначенню
точки екстремуму цільової функції
 (максимального значення критерію) і
обчисленню функціональних характеристик
СМО при знайденому
(максимального значення критерію) і
обчисленню функціональних характеристик
СМО при знайденому Знаходження оптимуму критерію здійснюється
за перебірним алгоритмом для послідовності
значень
Знаходження оптимуму критерію здійснюється
за перебірним алгоритмом для послідовності
значень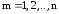 ,
в результаті чого знаходимо
,
в результаті чого знаходимо ,
при якому досягається максимальне
значення критерію
,
при якому досягається максимальне
значення критерію .
Оскільки величини
.
Оскільки величини постійні і додатні, то функція
постійні і додатні, то функція буде опуклою, отже існує єдине значення
буде опуклою, отже існує єдине значення ,
при якому
,
при якому досягає екстремуму.
досягає екстремуму.
Розглянемо СМО з такими значеннями
вхідних параметрів: інтенсивність
заявок на обслуговування від кожного
приладу
 інтенсивність обслуговування приладу
одним оператором –
інтенсивність обслуговування приладу
одним оператором – приладів на годину. Приведена інтенсивність
потоку заявок (кількість заявок, яка
приходиться на час обслуговування
однієї заявки) ρ=1/5=0,2 в годину. Прибуток
оператора від обслуговування однієї
заявки
приладів на годину. Приведена інтенсивність
потоку заявок (кількість заявок, яка
приходиться на час обслуговування
однієї заявки) ρ=1/5=0,2 в годину. Прибуток
оператора від обслуговування однієї
заявки грн., прибуток від роботи одного приладу
грн., прибуток від роботи одного приладу грн. Втрати від простою одного оператора
грн. Втрати від простою одного оператора грн., втрати від простою одного приладу
грн., втрати від простою одного приладу грн.
грн.
Знайдемо оптимальну кількість операторів
m, при яких загальний валовий прибуток
системи обслуговування буде максимальний
–
 .
.
Розв’язання. Дана СМО є
замкнутою. Імовірності її станів
визначаються за програмоюSmo_4. Пошук
точки екстремуму ,
при якій цільова функція
,
при якій цільова функція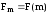 набуває максимального значення
набуває максимального значення здійснюємо за програмою Optim_1,
яка реалізує перебірний алгоритм пошуку
екстремуму функції дискретного аргументу.
Зауважимо, що у цій програмі, як і у
інших, у яких реалізуються перебірні
алгоритми, діапазон зміни параметра
оптимізації задається довільно, але
так, щоб шукане оптимальне значення
параметра приблизно попадало на середину
цього діапазону. У даному випадку
доцільно узяти проміжок зміни параметра
m від 1 до n.
здійснюємо за програмою Optim_1,
яка реалізує перебірний алгоритм пошуку
екстремуму функції дискретного аргументу.
Зауважимо, що у цій програмі, як і у
інших, у яких реалізуються перебірні
алгоритми, діапазон зміни параметра
оптимізації задається довільно, але
так, щоб шукане оптимальне значення
параметра приблизно попадало на середину
цього діапазону. У даному випадку
доцільно узяти проміжок зміни параметра
m від 1 до n.
Результати роботи програми Optim_1:
 вектор значень цільової функції;
вектор значень цільової функції;
 максимальне значення
максимальне значення

 оптимальне значення числа каналів
обслуговування.
оптимальне значення числа каналів
обслуговування.
Програма оптимізації Optim_1.

Алгоритм у Mathcad
Параметри СМО:
![]()
![]()
![]()

![]()
Показники прибутку і втрат:

2. Виклик програми Optim_1 (у цій програмі викликається підпрограма Smo_4):

3. Виведення
масиву значень цільової функції F(m),
оптимального значення кількості каналів
обслуговування
 і максимального значення цільової
функції
і максимального значення цільової
функції

![]()
![]()
![]()
![]()
![]()
4. Побудова графіка цільової функції
для
![]()

Рис 3.1. Графік цільової функції F(m)
Операційні характеристики СМО:
1. Кількість зайнятих операторів в одиницю часу (а також кількість обслужених заявок)

2. Кількість незайнятих операторів (операторів, які простоюють)

3. Кількість заявок у системі обслуговування (кількість заявок на обслуговуванні і у черзі)
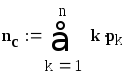
![]()
4. Кількість заявок поза системою (кількість працюючих заявок)

5. Абсолютна пропускна здатність системи (кількість заявок, яку може обслужити система)
![]()
![]()
6. Коефіцієнти простою приладів і операторів

Завдання для лабораторної роботи №1
СМО має m каналів
обслуговування, які обслуговують n
приладів. Інтенсивність заявок на
обслуговування від кожного приладу
дорівнює
 одиниць, інтенсивність обслуговування
приладу одним каналом –
одиниць, інтенсивність обслуговування
приладу одним каналом –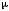 одиниць на годину. Приведена інтенсивність
потоку заявок (кількість заявок, яка
приходиться на час обслуговування
однієї заявки)
одиниць на годину. Приведена інтенсивність
потоку заявок (кількість заявок, яка
приходиться на час обслуговування
однієї заявки) в годину.
в годину.
Функціонування СМО пов’язано з двома видами прибутку:
 – прибуток СМО від обслуговування
однієї заявки;
– прибуток СМО від обслуговування
однієї заявки;
 – прибуток від роботи засобу виробництва,
який знаходиться у робочому стані, тобто
прибуток від роботи потенційних заявок
у СМО, які у даному випадку не проходять
обслуговування у СМО.
– прибуток від роботи засобу виробництва,
який знаходиться у робочому стані, тобто
прибуток від роботи потенційних заявок
у СМО, які у даному випадку не проходять
обслуговування у СМО.
СМО також несе економічні втрати від простою як каналів обслуговування так і засобів виробництва:
 – втрати, пов’язані з одиницею часу
простою каналу обслуговування;
– втрати, пов’язані з одиницею часу
простою каналу обслуговування;
 – втрати, пов’язані з одиницею часу,
проведеному засобом виробництва у
неробочому стані (це час чекання заявки
у черзі на обслуговування плюс час
обслуговування).
– втрати, пов’язані з одиницею часу,
проведеному засобом виробництва у
неробочому стані (це час чекання заявки
у черзі на обслуговування плюс час
обслуговування).
За критерій ефективності роботи СМО приймемо її годинний прибуток
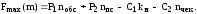
Визначити:
оптимальну кількість каналів
обслуговування
 при яких загальний валовий прибуток
системи обслуговування буде максимальний
–
при яких загальний валовий прибуток
системи обслуговування буде максимальний
–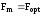 ;
;
функціональні характеристики оптимальної СМО;
Значення вартісних показників:
 .
.
