5. Контрольная работа № 8. Задания

1. (табл. 1).

а) доказать расходимость ряда, используя необходимое условие

сходимости;

б) исследовать на сходимость ряд, используя признаки сравнения;

в) исследовать на сходимость ряд, используя признак Даламбера;

г) исследовать на сходимость ряд, используя радикальный признак Коши.

2. Исследовать на сходимость ряд (табл. 2).

3. Найти область сходимости ряда (табл. 3).

4. Разложить функцию в ряд Тейлора в окрестности точки (табл. 4).

5. Записать комплексные числа в алгебраической, тригонометрической и показательной формах записи. Найти:

1) ; 2)(табл. 5).

6. Найти все значения корней из комплексного числа (табл. 6).

7. Для заданной функции найти действительную и мнимую части, т.е. представить функцию в виде: (табл. 7).

8. Записать в алгебраической форме заданное комплексное число (табл. 8).

9. Даны функции комплексного переменного и . Проверить выполнение условий Коши-Римана и в случае их выполнения найти (табл. 9).

10. Восстановить аналитическую функцию по известной действительной 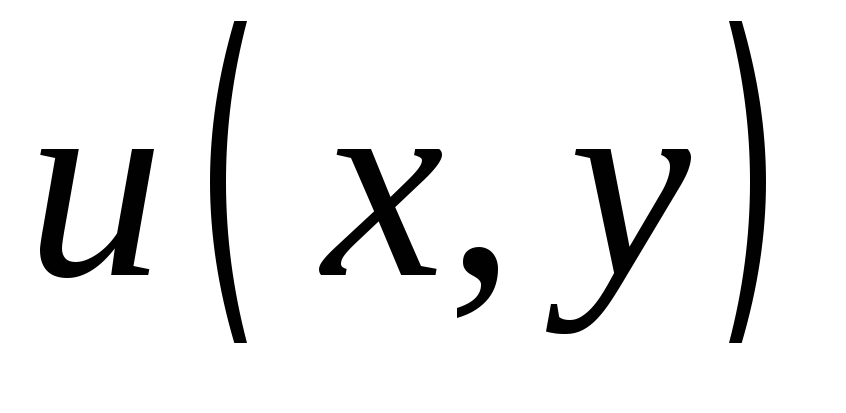или мнимой части и значению(табл. 10).

5.1. Пример выполнения контрольной работы № 8. Вариант № 0

Задание 1.

а) Доказать расходимость ряда , используя необходимое условие сходимости;

б) Исследовать на сходимость ряд , используя признаки сравнения;

в) Исследовать на сходимость ряд , используя признак Даламбера;

г) Исследовать на сходимость ряд , используя радикальный признак Коши.

Решение.

а) Согласно необходимому условию, если ряд сходится, то .

Имеем: .

Найдём :

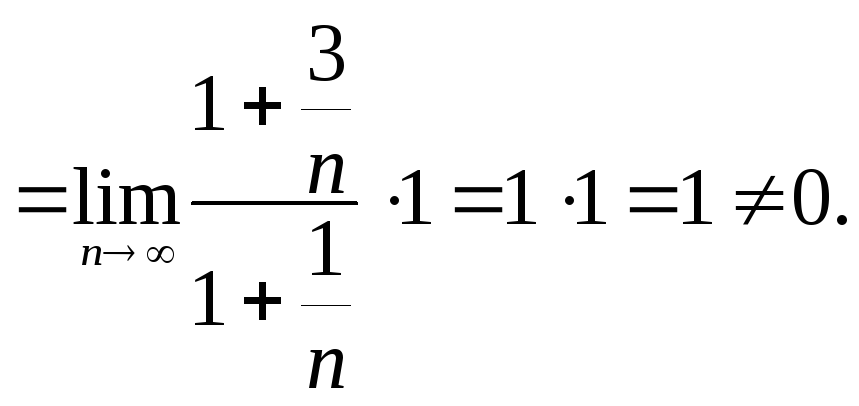
Так как не выполняется необходимое условие сходимости ряда, то ряд расходится.

б) Так как при, то согласно таблице эквивалентных бесконечно малых имеем:

Рассмотрим ряд:

,

который расходится, так как расходится ряд Дирихле .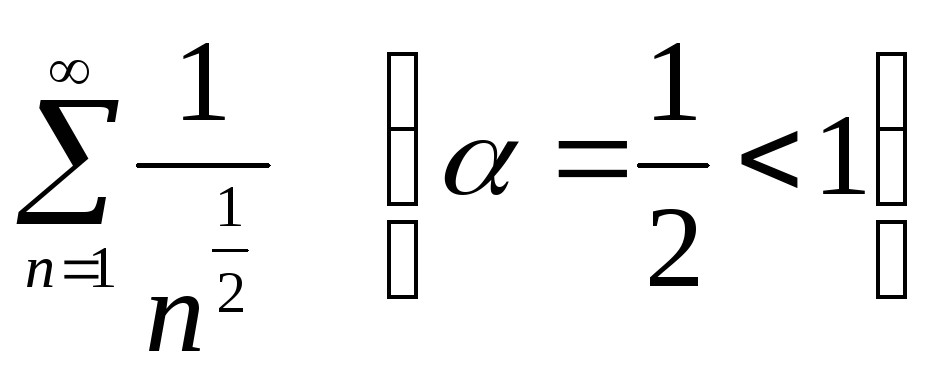

Применим второй признак сравнения. Для этого вычислим:

.

Следовательно, ряд также расходится.

в) имеем:

.

Тогда

.

Следовательно, по признаку Даламбера исследуемый ряд расходится.

г) имеем:

.

Тогда

.

Следовательно, по признаку Коши ряд сходится.

Задание 2. Исследовать на сходимость ряд .

Решение. Проверим, сходится ли данный знакочередующийся ряд абсолютно. Для этого исследуем на сходимость ряд, составленный из абсолютных величин членов данного ряда:

.

Применим к ряду из абсолютных величин признак Даламбера. Имеем:

.

Тогда

.

Следовательно, ряд сходится. А значит, рядсходится абсолютно.

Задание 3. Найти область сходимости ряда

Решение. Найдем сначала радиус сходимости степенного ряда по формуле:

.

Имеем: .

Тогда

.

Значит, интервалом абсолютной сходимости данного ряда будет интервал:

;

;

.

Исследуем сходимость ряда на концах интервала.

При , получим числовой ряд

.

1) Ряд не является абсолютно сходящимся, так как ряд , составленный из абсолютных величин членов данного ряда, являющийся рядом Дирихле с , расходится.

2) Используя признак Лейбница, исследуем ряд на условную сходимость. Для этого проверим выполнимость условий признака Лейбница для данного ряда:

1.

Очевидно, что данное неравенство верно для любого

2. .

Таким образом, для данного знакочередующегося ряда выполняются условия признака Лейбница, откуда следует, что ряд сходится условно.

При , получим числовой ряд

, который расходится.

Следовательно, – область сходимости ряда;

–область абсолютной сходимости ряда.

Задание 4.

Разложить функцию в ряд Тейлора в окрестности точки.

Решение: Преобразуем :

(*)

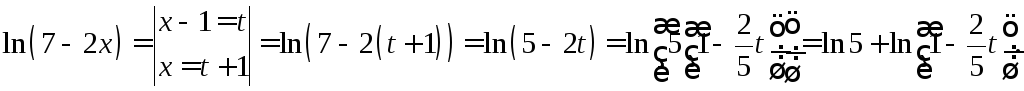Разложим в ряд Маклорена, заменяя нав известном разложении. Получаем:

.

Подставляя полученное разложение в (*) и возвращаясь к переменной получаем:

,

;

–интервал сходимости.

Задание 5. Записать комплексные числа в алгебраической, тригонометрической и показательной формах записи. Найти: 1) ; 2)

Решение. а) –алгебраическая форма записи комплексного числа

Находим модуль и аргумент комплексного числа . Здесь ,

Значит,

–тригонометрическая форма записи комплексного числа

–показательная форма записи комплексного числа

б) –алгебраическая форма записи комплексного числа

Находим модуль и аргумент комплексного числа . Здесь , Значит,

–тригонометрическая форма записи числа

–показательная форма записи комплексного числа

в) –алгебраическая форма записи комплексного числа

Находим модуль и аргумент комплексного числа :

Здесь ,

Значит,

–тригонометрическая форма записи комплексного числа

–показательная форма записи комплексного числа

Найдём:

1)

,т.е.получили комплексное числос действительной частью и мнимой частью

2)

, т.е. получили в результате комплексное число с действительной частью и мнимой частью

Задание 6. Найти все значения корней: .

Решение. Представим комплексное число в тригонометрической форме. Здесь

Поэтому

.

Используя формулу

находим:

где

Полагая получим:

Задание 7. Для заданной функции найти действительную и мнимую части, т.е. представить функцию в виде

Решение. Учитывая, что , получаем:

т.е.

Задание 8. Записать в алгебраической форме комплексное число

Решение. Используя формулу имеем:

Задание 9. Даны функции комплексного переменного и. Проверить выполнение условий Коши-Римана и в случае их выполнения найти

Решение. а) Имеем:

, так что

Для функций инайдём частные производные:

Условия Коши-Римана в этом случае имеют вид:

и удовлетворяются только в одной точке

Следовательно, функция дифференцируема только в точкеи нигде не аналитична.

Таким образом,

б) Имеем:

, так что

Для функций инайдём частные производные:

Условия Коши-Римана в этом случае имеют вид:

и выполняются во всех точках. Значит, функция всюду аналитическая. Тогда

Итак,

Задание 10. Восстановить аналитическую функцию по известной мнимой части и дополнительному условию

Решение. Имеем: По первому из условий Коши-Римана должно бытьтак что

Отсюда где функцияпока неизвестна.

Дифференцируя пои используя второе из условий Коши-Римана, получим:

а так как то

отсюда где

Итак, и, следовательно,

Таким образом, Постояннуюнайдём из условият.е., отсюда

Итак,