1. Определение выпуклой функции.

Кривая, заданная функцией y=f(x ) называется выпуклой в некотором интервале (a,b), если все точки кривой лежат не выше любой её касательной в этом интервале.

2. Определение вогнутой функции.

Кривая называется вогнутой на интервале (a,b), если все точки кривой лежат не ниже любой её касательной в этом интервале.

3. Определение точки перегиба.

Точка М(x₀, f(x₀)), лежащая на кривой и отделяющая выпуклую часть от вогнутой называется точкой перегиба.

4. Теорема 1 (дост. Усл-е выпуклости/вогнутости графика ф-ии)

Теорема 1: если во всех точках интервала (a,b) вторая производная функции отрицательна, то в этом интервале кривая выпукла, иначе вогнута. Отметим, что в точке перегиба вторая производная меняет знак, следовательно вторая производная равна нулю или не существует.

5. Теорема 2 (достаточный признак точки перегиба)

Теорема 2: если в точке х₀ вторая производная равна нулю или не существует, то и при переходе через эту точку f₀ меняет знак, то точка графика с абсциссой х₀ является точкой перегиба.

6. Схема полного исследования ф-ции. Уравнение асимптот.

Схема полного исследования функции. Построение графика.

1. Область определения функции

2. Точки разрыва функции. Вертикальные асимптоты (их сумма).

3. Чётность (нечётность), периодичность функции.

4. Монотонность и экстремумы функции.

5. Интервалы выпуклости, вогнутости функции и точки перегиба.

6. Горизонтальные и наклонные асимптоты.

7. Точки пересечения графика с осями координат.

8. При необходимости контрольные точки и построение графика.

  Уравнения асимптот: 

7. Определение первообразной функции

Определение: функцию F(x), заданную на промежутке, называют первообразной для функции f(x), заданную на том же промежутке, если F’(x)=f(x) для любого х из заданного промежутка.

8. Теорема о множестве всех первообразных

Теорема 1: о множестве всех первообразных: пусть для f(x) на некотором промежутке существует первообразная F(x), тогда f(x) имеет бесконечное множество первообразных, и все они имеют вид F(x)+C, где С – произвольная постоянная.

9. Определение неопределенного интеграла

Определение: множество всех первообразных для некоторой функции f(x) на заданном промежутке называется неопределённым интегралом от этой функции. ʃf(x)dx=F(x)+C.

10. 2 свойства неопределенного интеграла, вытекающие из определения

1. Дифференциал от неопределённого интеграла равен подынтегральному выражению, а производная от неопределённого интеграла равна подынтегральной функции.

2. Неопределённый интеграл от производной некоторой функции равен этой функции, сложенной с произвольной постоянной.

11. Свойства неопределенного интеграла

1. Постоянный множитель можно выносить за знак неопределённого интеграла.

2. Если существует интеграл ʃf₁(x)dx, ʃf₂(x)dx, то неопределённый интеграл от суммы (разности) функций равен сумме (разности) неопределённых интегралов от этих функций.

12. Интегрирование по частям в неопределенном интеграле (вывод формулы)

Этот метод основан на правиле дифференцирования произведений.

Пусть U,V дифференцируемы на некотором промежутке. Тогда d(UV)=UdV+VdU. Проинтегрируем это равенство.

∫ d(UV)= ∫ (UdV+VdU) символы интеграла и дифференциала уничтожают друг друга. Тогда

∫ d(UV)= ∫UdV+ ∫VdU следовательно ∫UdV=UV-∫VdU – эту формулу используют тогда, когда подынтегральное выражение VdU проще, чем UdV.

Например функция xⁿ проще, чем обратные функции: logx, arctgx, и т.д.

13. Замена переменных в неопределенном интеграле (вывод формулы)

Пусть F(x) – первообразная для f(x) (F’(x)=f(x)).

Тогда ∫f(x)dx=∫F’(x)dx, ∫dF(x)=F(x)+c.

В силу инвариантности определённого дифференциала (неизменности) формы дифференциала следует равенство dF(x)=F’(x)dx=f(x)dx. Справедлива не только в случае, когда х независимая переменная, но и когда х – дифференцируемая функция: х=∫(t).

∫f(x)dx=∫f(∫ (t))d(∫ (t))= ∫f(∫(t)) ∫’(t)dt=F(∫(t))+c

таким образом:

теорема 1:

Пусть F(x) – первообразная для f(x) на промежутке Х. функция х=∫(t) дифференцируема на промежутке Т, а значение этой функции Эх. Тогда F(∫(t)) будет первообразной f(x)∫’(t). тогда справедлива формула: ∫f(x)dx=∫f(∫(t))∫’(t)dt. F’(x)=f(x) dy=y’dx.

14. Методы интегрирования тригонометрических ф-ий

1. Интегралы вида ∫sinaxcosbxdx ∫sinaxsinbxdx ∫cosaxcosbxdx вычисляются с помощью применения формул произведения синусов и косинусов.

2. Интеграл вида: ∫sin^mxcosⁿxdx

А) если м и н нечётные положительные, то применяется основное тригонометрическое тождество, подведение под знак дифференциала.

Б) если м и н чётное положительное число (0), то применяем формулы понижения степени.

В) если м+н чётное отрицательное число, то делаем замену tgx=t.

3) интегралы вида ∫tgⁿxdx ∫ctgⁿxdx вычисляются подстановкой (заменой) соответствующей функцией на новую переменную (tgx=t). Универсальная тригонометрическая подстановка (вывод формул)

15. Универсальная тригонометрическая подстановка.

3) интегралы вида ∫tgⁿxdx ∫ctgⁿxdx вычисляются подстановкой (заменой) соответствующей функцией на новую переменную (tgx=t). В общем случае можно применить универсальную тригонометрическую подстановку: sinx=2sin(x/2)cos(x/2)=2(sin(x/2)/cos(x/2)*cos²(x/2)=2tg(x/2)*cos(x/2)=2tg(x/2)*(1/(1+tg(x/))=2t/1+t².

Cosx=(1-t²)/(1+t²). Tg(x/2)=t x/2=arctgt x=2arctgt dx=2/(1+t²)dt

16. Интегрирование простейших иррациональных ф-ий

1. Интеграл ∫R(x, корень m-ный из х, корень к-тый из х…)dx

Обозначим через n- наиментшее кратное чисел k,m тогда n/k, n/m будут целые числа. Исходный интеграл вычисляется путём замены переменной х=tⁿ dx=n*t^n-1dt

2. ∫((Ax+B)dx/(x-α)√(ax²+bx+c) вычисляются с помощью замены (x-α)=1/t

3. ∫R(x,√(a²-x²))dx замена х=asint ( x=acost)

∫R(x,√(a²+x²))dx замена x=atgt (x=actgt)

∫R(x,√( x²-a²))dx замена x=a/cost (x=a/sint)

17. Интегрирование рациональных дробей (правило разложения)

Всякая рациональная функция R(x) может быть представлена в виде дроби P(x)/Q(x) где P и Q – многочлен. (R(x)=P(x)/Q(x)). Заметим, что если степень числит. m> или = степени знаменателя n, то разделив многочлен P и Q в частном получим N(x) и в остатке 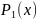. Степень которого будет не выше чем (n-1). таким образом при интегрировании рациональной функции мы рассмотрим случай так называемой правильной дроби, т.е. такой дроби у которой в степени числителя строго меньше степени знаменателя.

Пусть Q(x) представлен в виде производной линейных и квадратичных множителей тогда можно представить в виде простейших дробей первого и второго вида.

1. 2) где Ai, Bi, Ci -const

Правило разложения: к каждому множителю представлен знаменатель (в степени) q соответственно к слагаемых дробей 1-го вида а каждому множителю соответственно сумма t дробей второго вида . Например пусть знаменатель q был разложен на множители P(x)/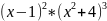 тогда согласно правилу =