3.7. Ряды Тейлора

Мы рассматривали степенные ряды вида

или

Каждый из таких рядов в своей области сходимости сходится к некоторой функции, сумме степенного ряда. Для приложений важно уметь данную функцию разлагать в степенной ряд, т.е. функциюпредставлять в виде суммы степенного ряда.

Как известно, для любой функции , определённой в окрестности точкии имеющей в ней производные до-го порядка включительно, справедливаформула Тейлора:

, (10)

где –остаточный член в форме Лагранжа. Число можно записать в виде, где.

Формулу (10) кратко можно записать в виде

,

где –многочлен Тейлора.

Если функция имеет производные любых порядков ( т.е. бесконечно дифференцируема ) в окрестности точки, то в формуле Тейлора мы можем использовать сколь угодно много членов. Тогда формула (10) примет вид:

. (11)

Определение. Ряд в разложении (11), называется рядом Тейлора для функции , а коэффициенты этого степенного ряда

называются коэффициентами Тейлора.

Если в ряде Тейлора положить , то получим разложение функции по степенямв так называемыйряд Маклорена:

Замечание. В ряд Тейлора можно разложить любую бесконечно дифференцируемую в окрестности точки функции. Это является необходимым условием разложения функциив ряд Тейлора. Но отсюда ещё не следует, что он будет сходиться к данной функции; он может оказаться расходящимся или сходящимся, но не к функции.

Теорема. Для того чтобы при некотором значении имело место разложение (11), необходимо и достаточно, чтобы при этом значенииостаточный член формулы Тейлора (10) стремился к нулю при неограниченном возрастании, т.е. чтобы

.

Способы разложения функции в ряд Тейлора

1. Непосредственное разложение

Для разложения функции в ряд Тейлора нужно:

а) найти все производные до порядка включительно:

;

б) вычислить значения производных в точке ;

в) составить ряд ;

г) найти радиус сходимости степенного ряда и интервал сходимости;

д) доказать, что остаточный член ряда при,;

е) Таким образом, при.

2. Косвенное разложение

В этом случае используют уже известные разложения и, применяя метод подстановки, получают разложения для других рядов.

Приведём разложения основных элементарных функций в ряд Маклорена:

1. ,;

2. ,;

3. ,;

4. ,;

5. ,;

6.

,;

В частности,

а) ;

б) ;

7. ,;

8.

, ;

9. ,.

Пример 12. Разложить в ряд Маклорена функцию , пользуясь косвенным методом.

Решение. Заменяя нав разложении 6, получим:

, .

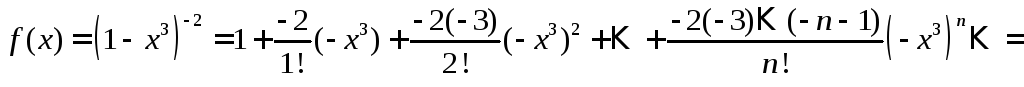
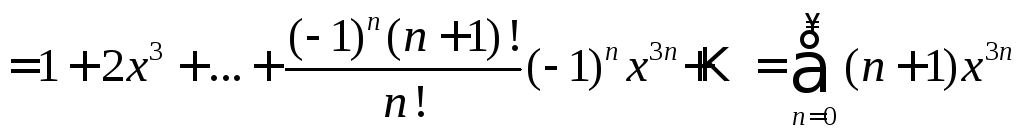Пример 13. Разложить функцию в ряд Тейлора в окрестности точки(по степеням).

Решение. Разложим функцию на сумму простейших дробей:

.

Найдём :

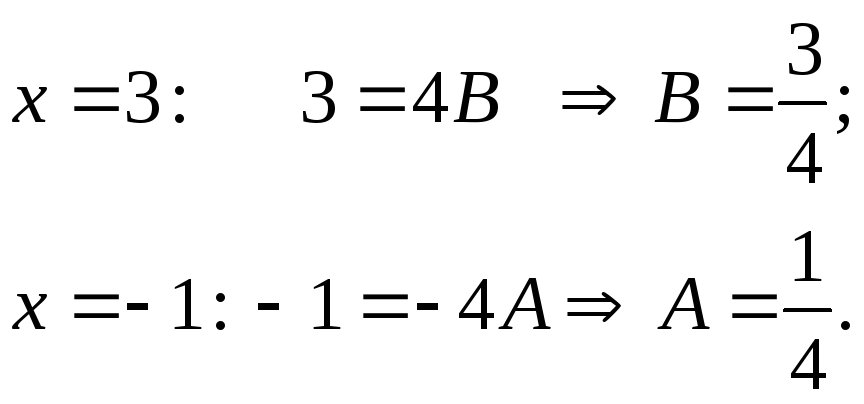
Таким образом,

.

Разложим дроби ив ряд Тейлора по степеням, используя разложения 6а) и 6б) :

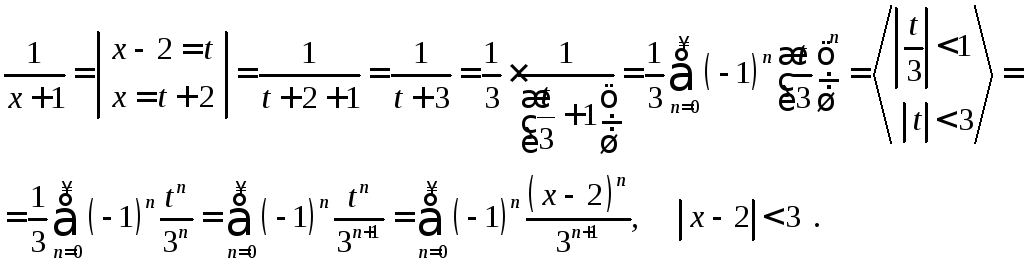
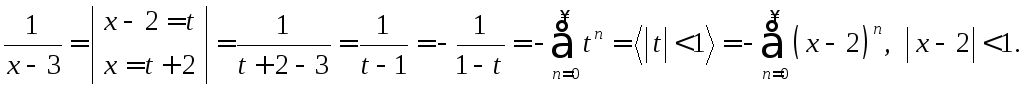Следовательно, разложение функции в ряд Тейлора по степенямимеет вид:

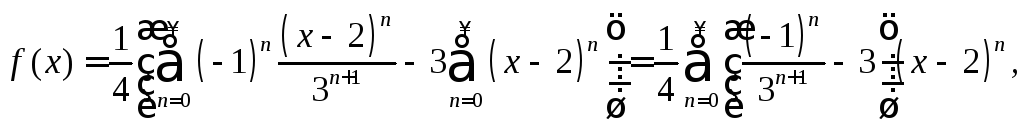где

–интервал сходимости.

4. Основы теории функций комплексного переменного