
- •3. Числовые и функциональные ряды
- •3.1. Числовые ряды: основные определения
- •3.2. Простейшие свойства числовых рядов. Необходимый признак сходимости
- •3.3. Признаки сходимости числовых рядов с положительными членами
- •3.4. Знакопеременные ряды. Абсолютная и условная сходимость
- •3.5. Функциональные ряды: основные определения
- •3.6. Степенные ряды
- •3.7. Ряды Тейлора
- •4. Основы теории функций комплексного переменного
- •4.1. Комплексные числа: определение, алгебра комплексных чисел, алгебраическая форма записи
- •4.2. Геометрическое изображение комплексных чисел. Тригонометрическая и показательная формы записи комплексного числа
- •4.3. Формула Муавра и извлечение корня п-ой степени из комплексного числа
- •4.4. Функции комплексного переменного
- •1. Показательная функция
- •2. Логарифмическая функция
- •3. Тригонометрические функции
- •4. Гиперболические функции
- •5. Обратные тригонометрические функции
- •6. Общая степенная функция
- •4.5. Дифференцирование функций комплексного переменного. Аналитические функции
- •5. Контрольная работа № 8. Задания
- •5.1. Пример выполнения контрольной работы № 8. Вариант № 0
- •5.2. Варианты заданий контрольной работы № 8
- •Рекомендуемая литература
2. Логарифмическая функция
Функция, обратная
к показательной функции
![]() ,
называется логарифмической и обозначается
,
называется логарифмической и обозначается
![]() .
.
Она определена
для любого
![]() и
и![]() .
.
Пусть
![]() тогда
тогда![]() и из свойств показательной функции
имеем:
и из свойств показательной функции
имеем:![]()
Получаем:
![]()
Эта функция является
многозначной. Главным значением
![]() называется то значение, которое получается
при
называется то значение, которое получается
при![]() ;
оно обозначается
;
оно обозначается
![]() .
.
Тогда
![]()
Справедливы следующие соотношения:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() где
где![]()
3. Тригонометрические функции
Функции
![]() и
и![]() для
для![]() определяются формулами:
определяются формулами:
![]()
Свойства:
Непрерывны на всей комплексной плоскости;
Периодичны с периодом
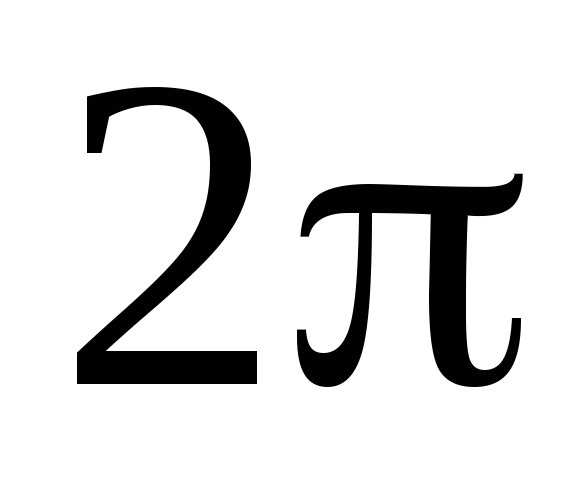 ,
т.е.
,
т.е.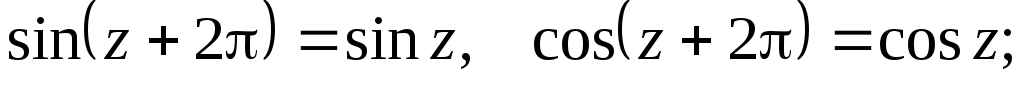
Принимают любые значения, т.е. уравнения
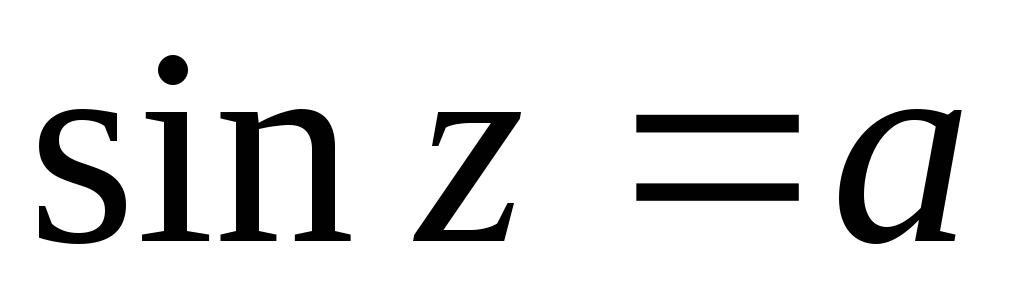 и
и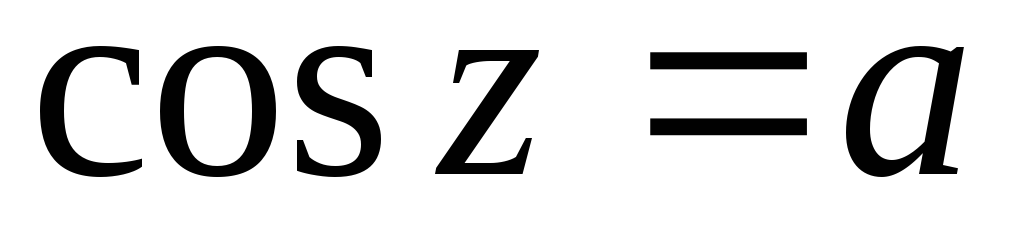 имеют решения для любого комплексного
числа
имеют решения для любого комплексного
числа ;
;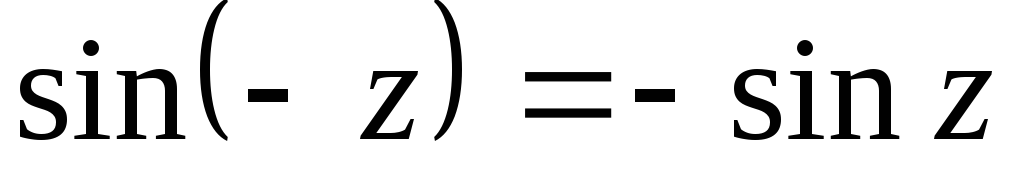 –нечётная функция,
–нечётная функция,
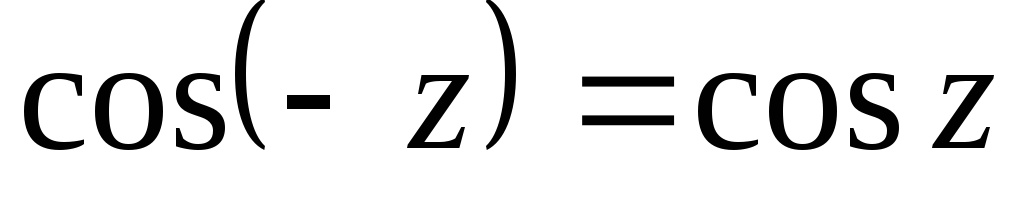 –
чётная функция;
–
чётная функция;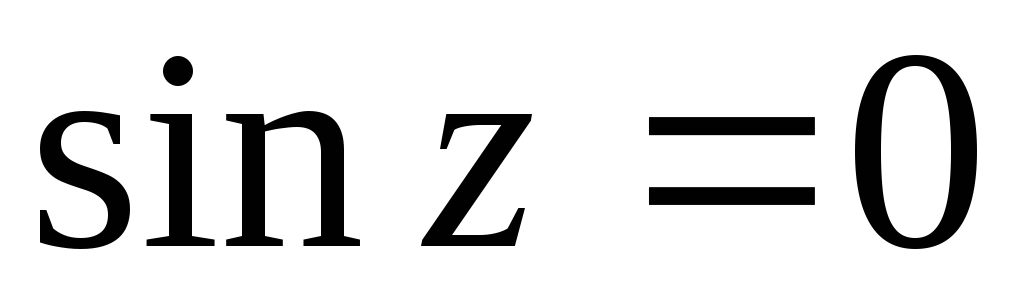 при
при
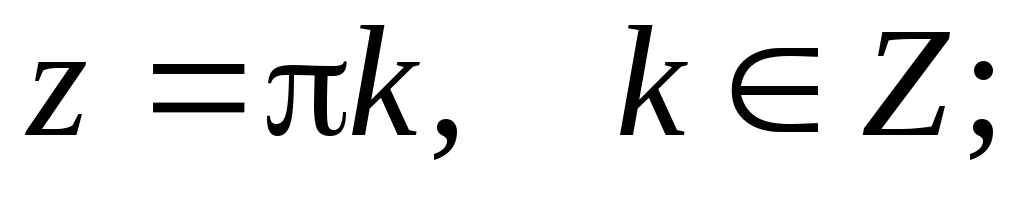
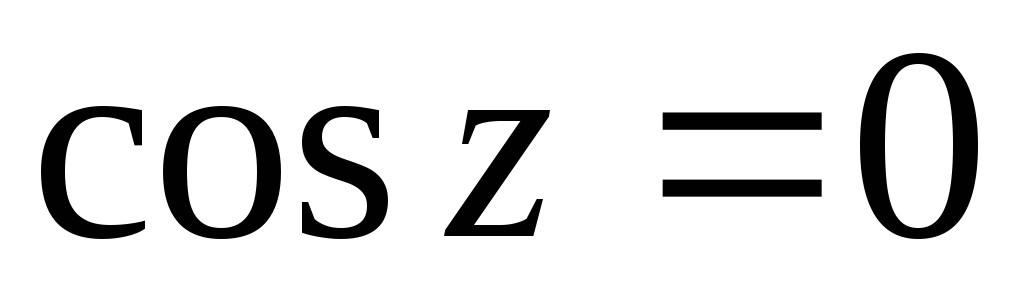 при
при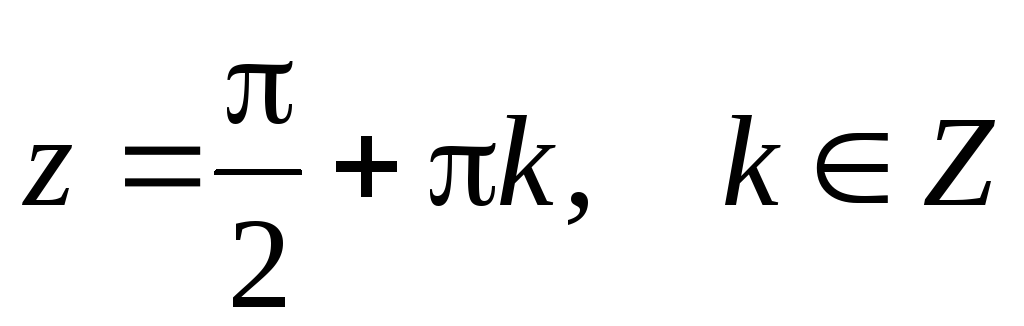 ;
;Все тригонометрические формулы для действительного аргумента
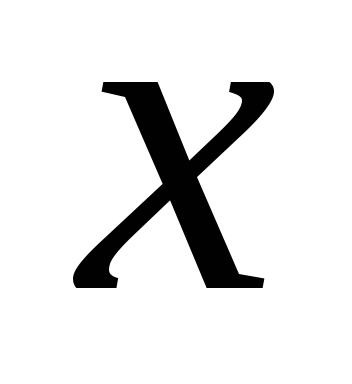 справедливы и для комплексного аргумента
справедливы и для комплексного аргумента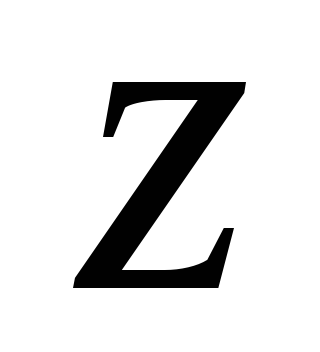 ,
например:
,
например:
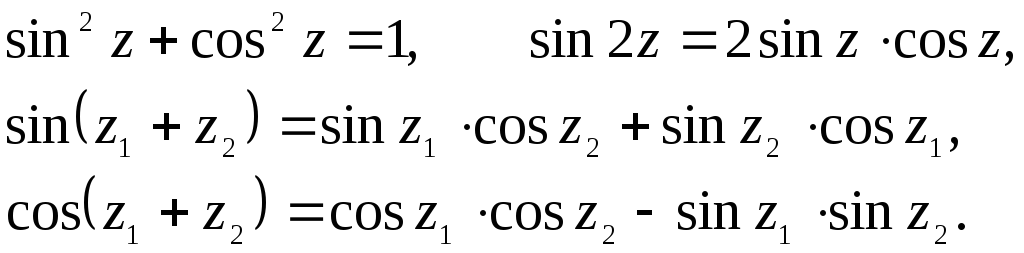
Функции
![]() и
и![]() определяются формулами:
определяются формулами:
![]()
![]() непрерывна при
непрерывна при
![]()
![]() непрерывна при
непрерывна при
![]()
4. Гиперболические функции
Функции
![]() (гиперболический синус) и
(гиперболический синус) и![]() (гиперболический косинус) комплексного
переменного определяются формулами:
(гиперболический косинус) комплексного
переменного определяются формулами:
![]()
т.е.
![]()
Гиперболические
тангенс
![]() и котангенс
и котангенс![]() определяются формулами:
определяются формулами:
![]()
Свойства
гиперболических функций вытекают из
свойств
![]() и
и![]() ,
все формулы, справедливые при действительных
значениях
,
все формулы, справедливые при действительных
значениях![]() справедливы и для комплексных значений
справедливы и для комплексных значений![]() ,
например:
,
например:
![]() .
.
5. Обратные тригонометрические функции
Функции
![]() определяются как функции, обратные
соответствующим тригонометрическим
функциям.
определяются как функции, обратные
соответствующим тригонометрическим
функциям.
Например, если
![]() ,
то
,
то![]() называется арксинусом числа
называется арксинусом числа![]() и обозначается
и обозначается![]()
Все эти функции являются многозначными и выражаются через логарифмическую функцию:
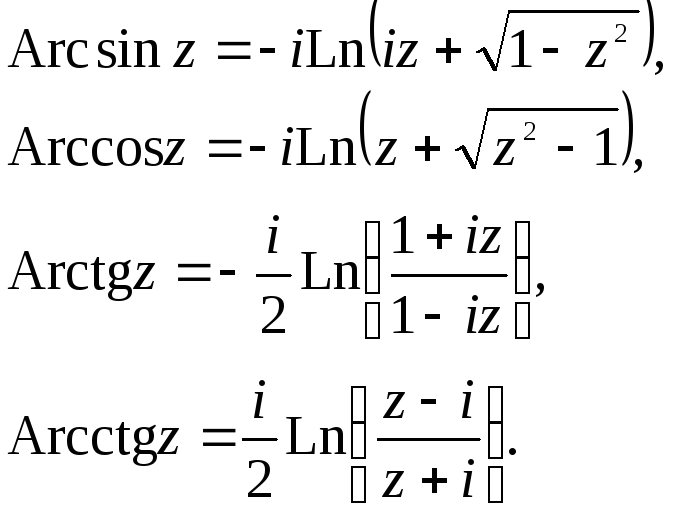
6. Общая степенная функция
Степенная функция
![]() для натуральногоп
определяется
формулой Муавра:
для натуральногоп
определяется
формулой Муавра:
![]() .
.
Если же показатель является комплексным числом, то такая функция называется общей степенной и определяется формулой:
![]() ,
где
,
где
![]() – комплексное число.
– комплексное число.
Для этой функции несправедливы свойства:
![]()
Пример 6. Для
данных функций найти действительную
часть
![]() и мнимую часть
и мнимую часть![]() :
а)
:
а)![]() б)
б)![]() ;
в)
;
в)![]()
Решение. а)
Учитывая, что
![]() ,
получаем:
,
получаем:
![]()
т.е.
![]()
б)
![]()
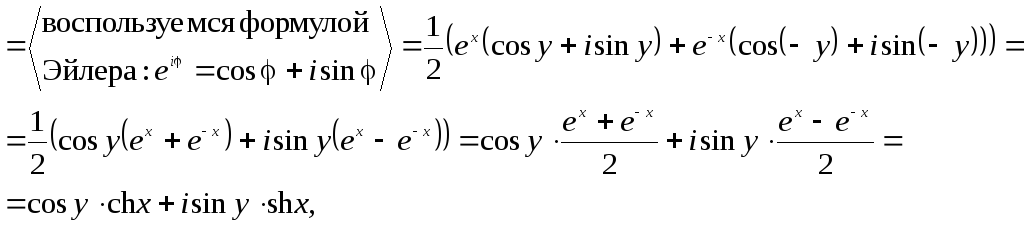
т.е.
![]()
в)
![]()
т.е.
![]()
Пример 7. Записать
в алгебраической форме следующие
комплексные числа: а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Решение. а)
Используя формулу
![]() получим:
получим:
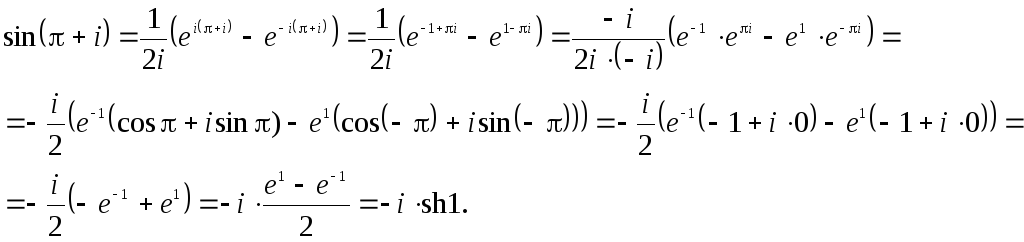 Таким образом,
мы представили число
Таким образом,
мы представили число
![]() в алгебраической форме:
в алгебраической форме:![]() ,
где
,
где![]() .
.
б) Имеем общую
степенную функцию, так как в степени
стоит комплексное число. Применяя
формулу
![]() ,
получим:
,
получим:
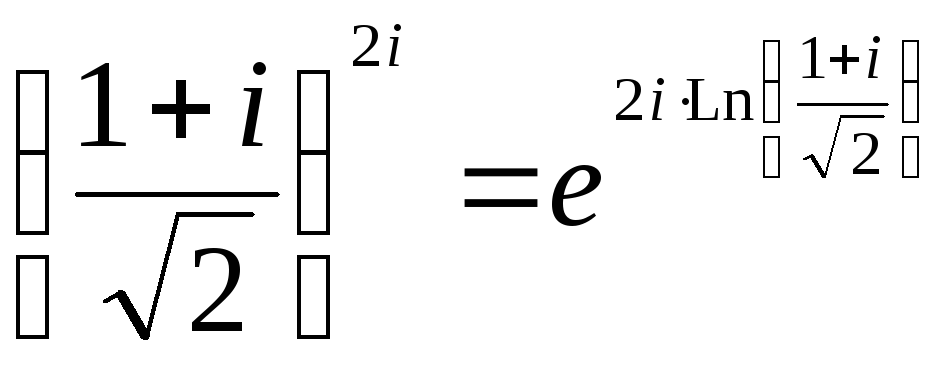 .
.
Вычислим отдельно
![]() ,
используя формулу:
,
используя формулу:![]() :
:
![]() .
Здесь
.
Здесь
![]()
![]() Тогда
Тогда
![]()
Окончательно получаем:
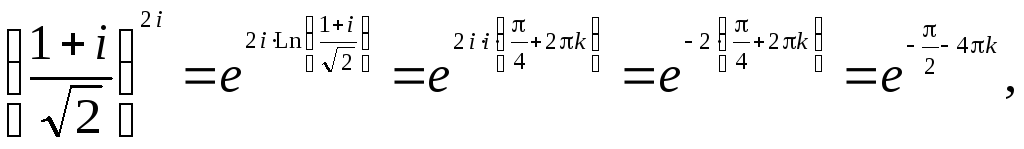 где
где
![]()
Получили комплексное
число, записанное в алгебраической
форме, у которого
![]()
в) Используя
формулу
![]() получим:
получим:
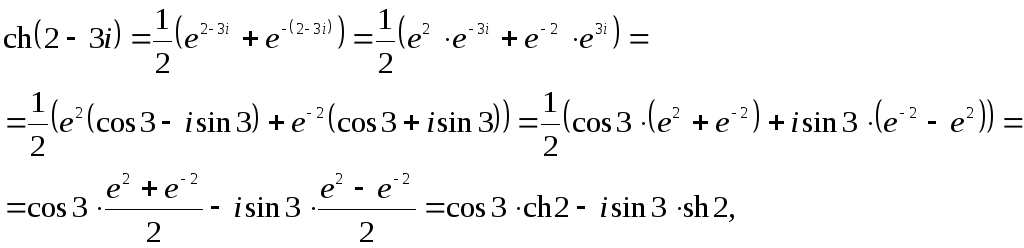
т.е. получили
комплексное число с действительной
частью
![]() и мнимой частью
и мнимой частью![]()
4.5. Дифференцирование функций комплексного переменного. Аналитические функции
Пусть функция
![]() определена в некоторой области
определена в некоторой области![]() комплексного переменного
комплексного переменного![]() .
Пусть точки
.
Пусть точки![]() и
и![]() принадлежат области
принадлежат области![]() .
Обозначим:
.
Обозначим:
![]()
Определение.
Функция
![]() называется дифференцируемой в точке
называется дифференцируемой в точке![]() ,
если отношение
,
если отношение![]() имеет конечный предел при
имеет конечный предел при![]() произвольным образом. Этот предел
называется производной функции
произвольным образом. Этот предел
называется производной функции![]() и обозначается символом
и обозначается символом![]() (или
(или![]() ,
или
,
или![]() ),
так что по определению
),
так что по определению
![]()
Если
![]() ,
то в каждой точке дифференцируемости
функции
,
то в каждой точке дифференцируемости
функции![]() выполняются соотношения:
выполняются соотношения:
![]()
называемые условиями Коши-Римана.
Обратно, если в
некоторой точке
![]() функции
функции![]() и
и![]() дифференцируемы как функции действительных
переменных
дифференцируемы как функции действительных
переменных![]() и
и![]() и, кроме того, удовлетворяют условиям
Коши-Римана, то функция
и, кроме того, удовлетворяют условиям
Коши-Римана, то функция![]() является дифференцируемой в точке
является дифференцируемой в точке![]() как функция комплексного переменного
как функция комплексного переменного![]() .
.
Определение.
Функция
![]() называется аналитической в данной точке
называется аналитической в данной точке![]() ,
если она дифференцируема как в самой
точке
,
если она дифференцируема как в самой
точке![]() ,
так и в некоторой её окрестности. Функция
,
так и в некоторой её окрестности. Функция![]() называется аналитической в области
называется аналитической в области![]() ,
если она дифференцируема в каждой точке
этой области.
,
если она дифференцируема в каждой точке
этой области.
Для любой
аналитической функции
![]() имеем:
имеем:
![]() .
.
Пример 8. Показать,
что функция
![]() является аналитической на всей комплексной
плоскости.
является аналитической на всей комплексной
плоскости.
Решение.
Имеем:
![]() ,
так что
,
так что
![]()
Для функций
![]() и
и![]() проверим выполнение условий Коши-Римана:
проверим выполнение условий Коши-Римана:
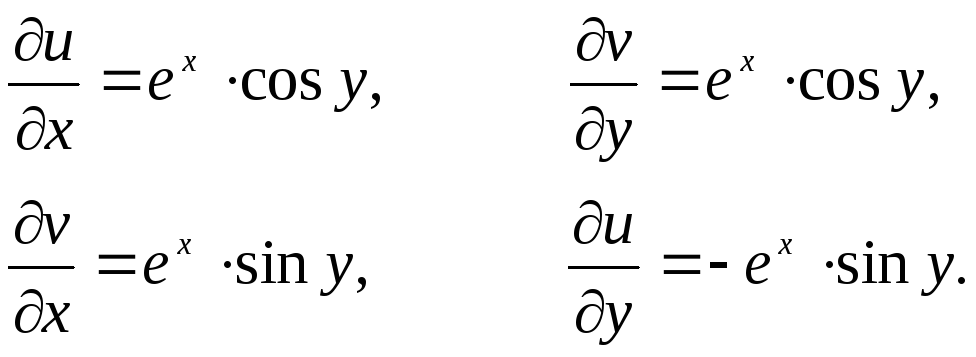
Условия Коши-Римана
выполняются во всех точках. Значит,
функция
![]() всюду аналитическая. Тогда
всюду аналитическая. Тогда
![]()
Итак,
![]()
Пример 9. Является
ли функция
![]() аналитической хотя бы в одной точке?
аналитической хотя бы в одной точке?
Решение. Имеем:
![]() ,
так что
,
так что
![]()
Найдём частные
производные функций
![]() и
и![]() :
:
![]()
Условия Коши-Римана в этом случае имеют вид:
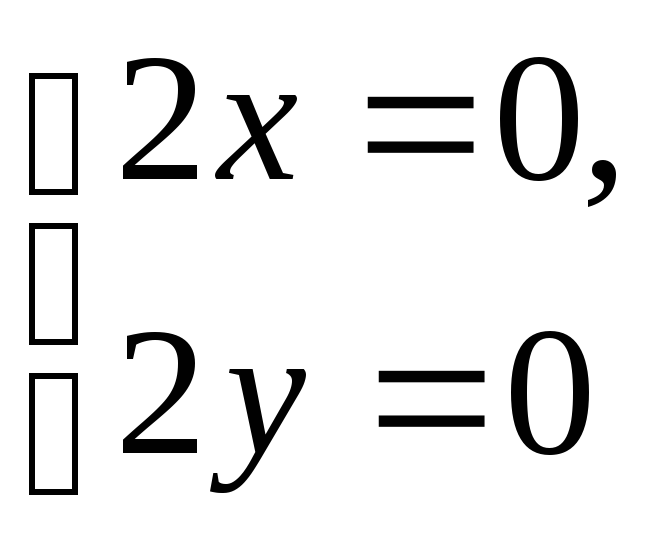
и удовлетворяются
только в одной точке
![]()
Следовательно,
функция
![]() дифференцируема только в точке
дифференцируема только в точке![]() и нигде не аналитична.
и нигде не аналитична.
Таким образом,
![]()
Для производных
от функций комплексного переменного
имеют место правила, аналогичные
соответствующим правилам для производных
от функций действительного переменного.
А именно: если в точке
![]() существуют производные
существуют производные![]() и
и![]() ,
то существуют и производные
,
то существуют и производные![]() ,
,![]() ,
,![]() ,
,![]() ,
причём выполняются следующие равенства:
,
причём выполняются следующие равенства:
![]() где
где
![]() – комплексное число;
– комплексное число;
![]()
![]()
![]() (при
(при
![]() ).
).
Производные основных элементарных функций находятся по тем же формулам, что и для действительного аргумента:
-
1.
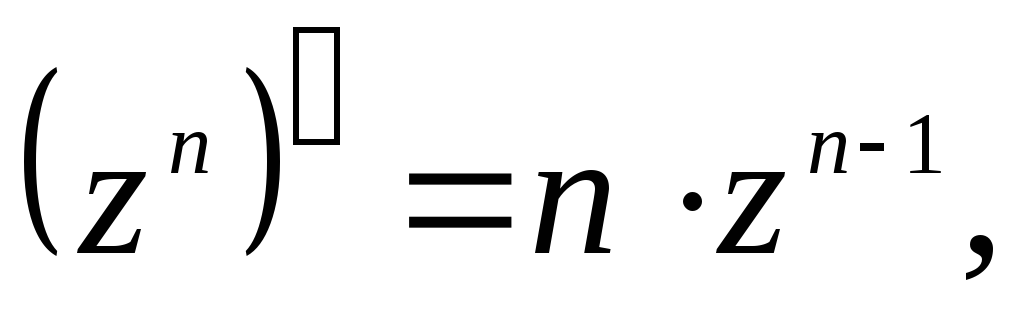
7.
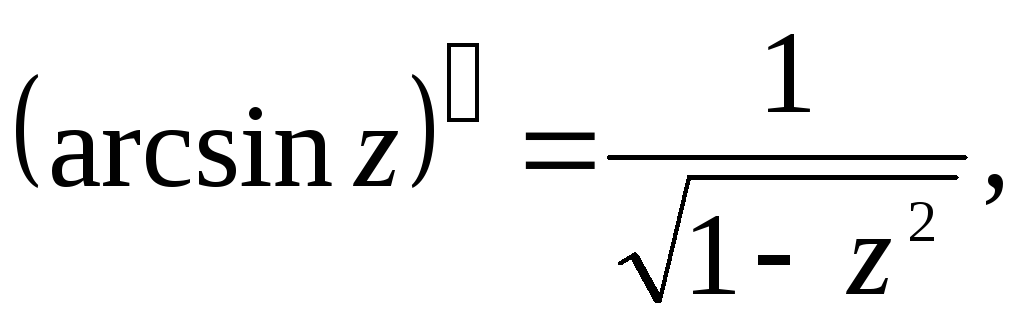
2.
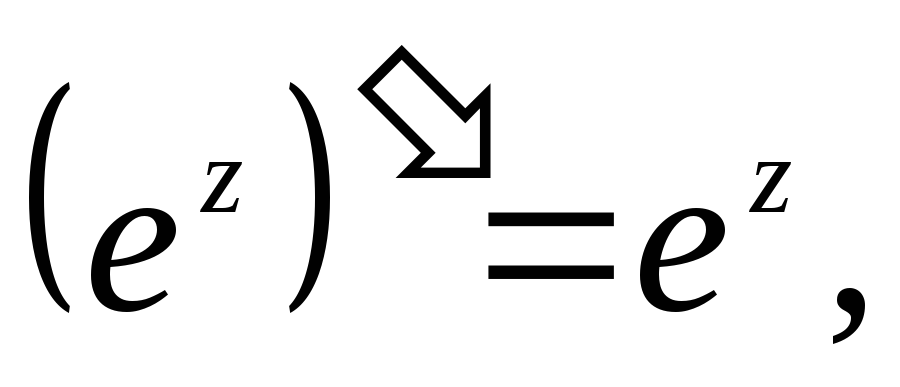
8.
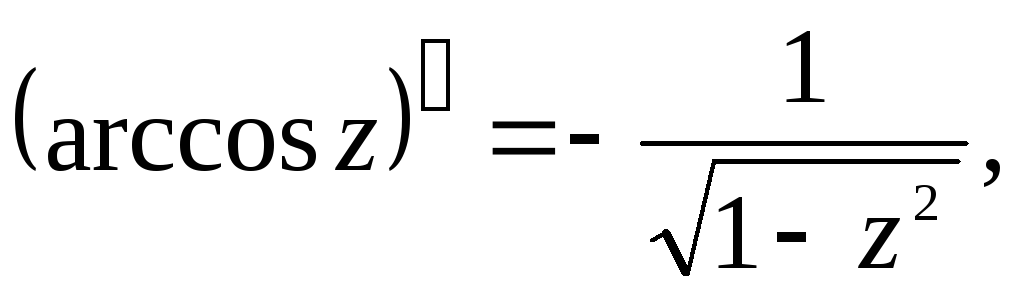
3.
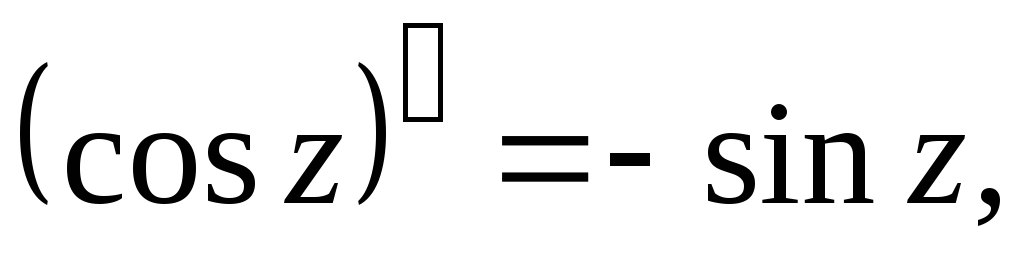
9.
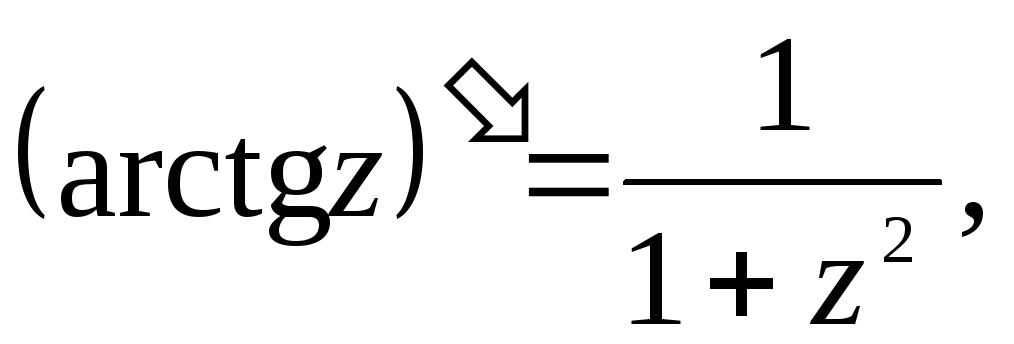
4.
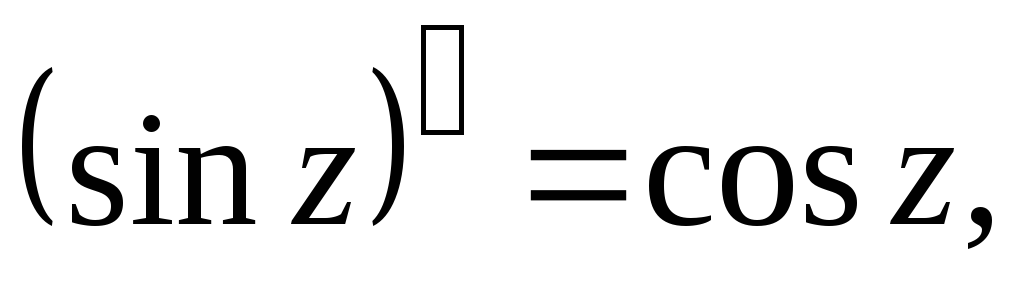
10.
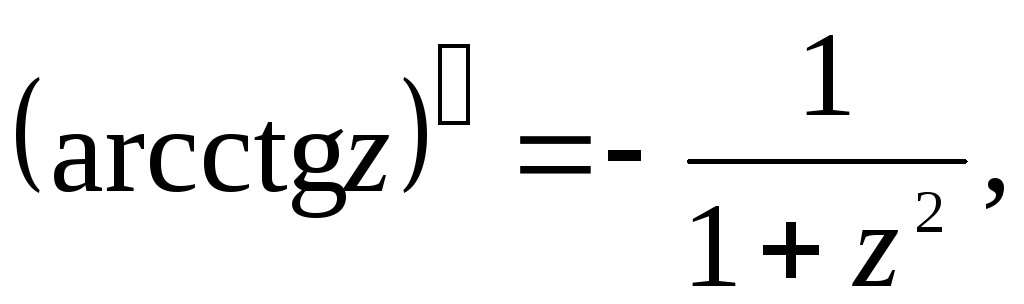
5.
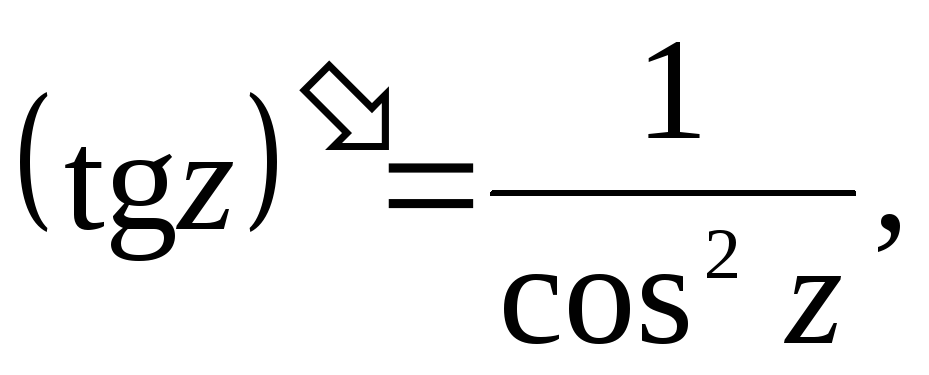
11.
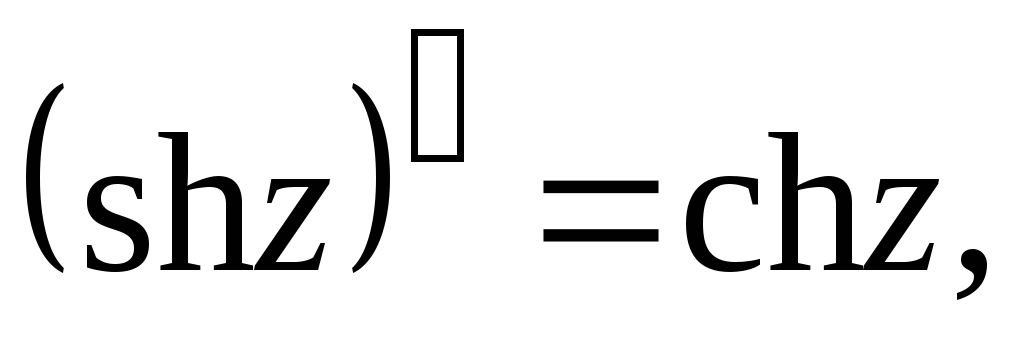
6.
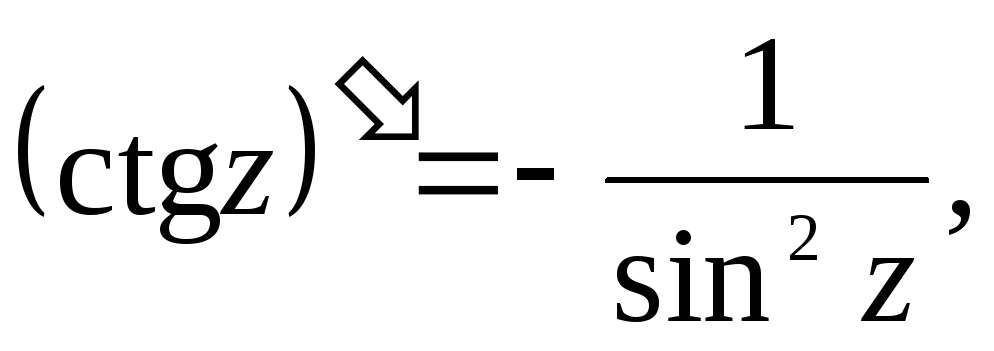
12.
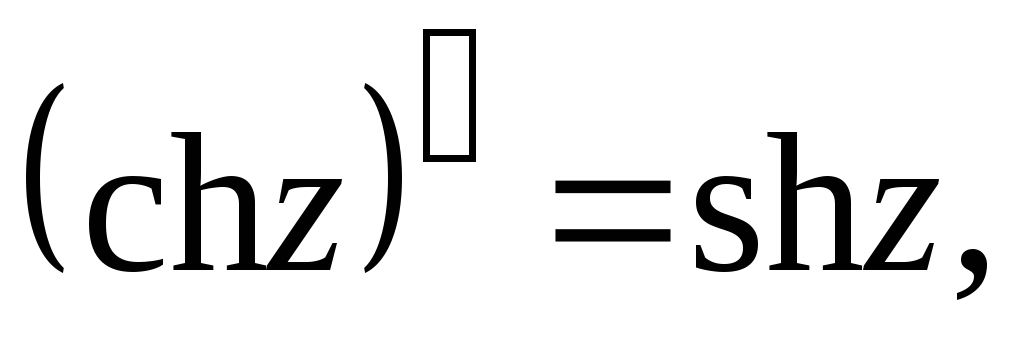
7.
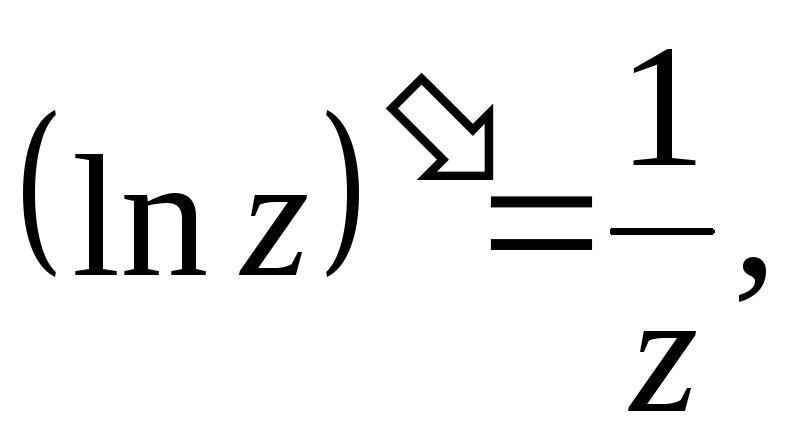
13.
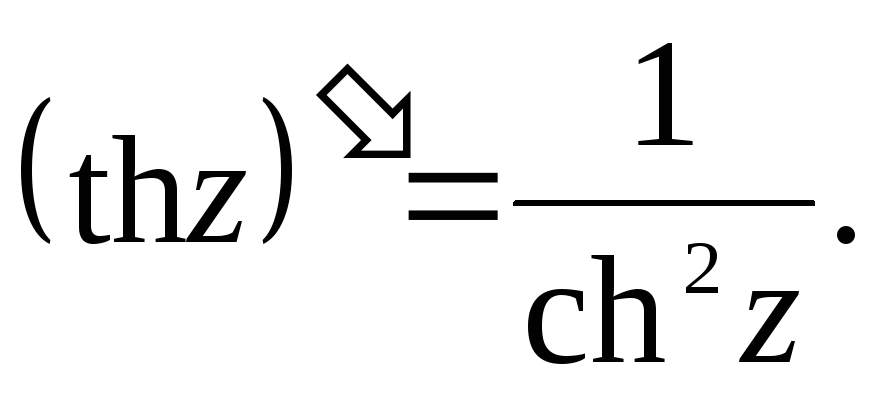
Если функция
![]() – аналитическая в области
– аналитическая в области![]() ,
то её действительная часть
,
то её действительная часть![]() и мнимая часть
и мнимая часть![]() являются функциями,гармоническими
в области
являются функциями,гармоническими
в области
![]() .
Это значит, что у каждой из функций
.
Это значит, что у каждой из функций![]() и
и![]() существуют непрерывные в
существуют непрерывные в![]() частные производные 2-го порядка, и для
каждой из них верноуравнение
Лапласа:
частные производные 2-го порядка, и для
каждой из них верноуравнение
Лапласа:
![]()
Если функция
![]() (функция
(функция![]() )
является гармонической в некоторой
области
)
является гармонической в некоторой
области![]() (вообще говоря, односвязной, т.е.
ограниченной замкнутой несамопересекающейся
линией), то существует аналитическая в
(вообще говоря, односвязной, т.е.
ограниченной замкнутой несамопересекающейся
линией), то существует аналитическая в![]() функция
функция![]() с действительной частью
с действительной частью![]() (соответственно, с мнимой частью
(соответственно, с мнимой частью![]() ),
определяемая с точностью до постоянного
слагаемого.
),
определяемая с точностью до постоянного
слагаемого.
Пользуясь условиями
Коши-Римана, аналитическую функцию
![]() можно восстановить, если известна её
действительная часть
можно восстановить, если известна её
действительная часть![]() или мнимая часть
или мнимая часть![]() .
.
Пример 10.
Восстановить
функцию
![]() по известной её действительной части
по известной её действительной части![]() и дополнительном условии
и дополнительном условии![]()
Решение. Проверим,
является ли функция
![]() гармонической.
гармонической.
Имеем:
![]() Вычислим частные производные 2-го
порядка:
Вычислим частные производные 2-го
порядка:
![]()
Отсюда
![]() т.е. функция
т.е. функция![]() удовлетворяет уравнению Лапласа, а,
значит, является гармонической.
удовлетворяет уравнению Лапласа, а,
значит, является гармонической.
Имеем:
![]() По первому из условий Коши-Римана должно
быть
По первому из условий Коши-Римана должно
быть![]() так что
так что![]()
Отсюда
![]() где функция
где функция![]() пока неизвестна.
пока неизвестна.
Дифференцируя
![]() по
по![]() и используя второе из условий Коши-Римана,
получим:
и используя второе из условий Коши-Римана,
получим:
![]() а так как
а так как
![]() то
то
![]() отсюда
отсюда
![]() а значит
а значит![]() где
где![]()
Итак,
![]() и, следовательно,
и, следовательно,
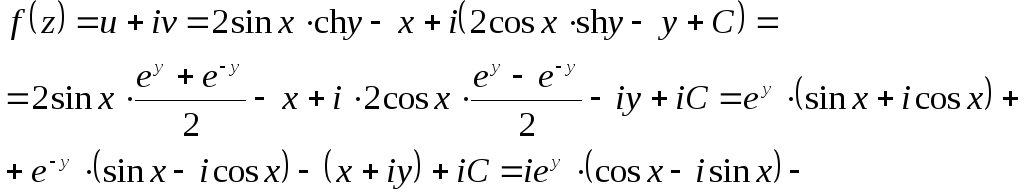
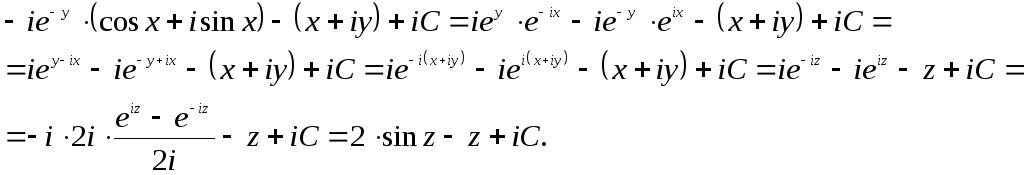
Таким образом,
![]() Постоянную
Постоянную![]() найдём из условия
найдём из условия![]() т.е.
т.е.![]() ,
отсюда
,
отсюда![]()
Ответ:
![]()
