4.3. Формула Муавра и извлечение корня п-ой степени из комплексного числа

Вычислив произведение комплексных чисел, записанных в тригонометрической форме, можно убедиться, что модуль и аргумент комплексного числа обладают следующими свойствами:

. Модуль произведения комплексных чисел равен произведению модулей этих чисел: .

. Аргумент произведения комплексных чисел равен сумме аргументов этих чисел: .

Используя эти свойства, легко можно получить формулу возведения комплексного числа в целую положительную степень, а именно:

если , то

–формула Муавра,

или в показательной форме записи:

.

Определение. Корнем п-ой степени из комплексного числа называется такое комплексное число, которое, будучи возведено в степеньп даст число .

Из определения и формулы Муавра ясно, что модуль искомого корня будет , а аргумент

Таким образом,

(1)

Придавать значения, большие, не имеет смысла, так как будем получать уже имеющиеся значения аргумента (с точностью до).

Следовательно, корень п-ой степени из комплексного числа имеетп различных значений, модули которых одинаковы (), т.е. все значения корня лежат на окружности с центром в начале координат радиуса, а аргументы последовательных значений отличаются на угол.

Пример 4. Используя формулу Муавра, вычислить:

а) ; б)

Решение. а) Представим число в тригонометрической форме. Имеем:

. Значит,

–тригонометрическая форма записи комплексного числа .

Применяя формулу Муавра, получим:

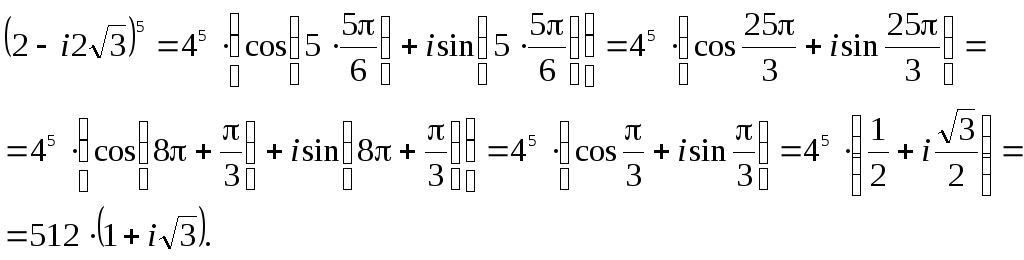
б) Представим число в тригонометрической форме. Имеем:. Поэтому

–тригонометрическая форма записи комплексного числа .

Применяя формулу Муавра, получим:

Пример 5. Найти все значения корня: .

Решение. Представим комплексное число в тригонометрической форме. ЗдесьПоэтому

.

По формуле (1) находим:

где

Полагая , получим:

Найденным корням соответствуют вершины правильного пятиугольника, вписанного в окружность радиуса с центром в начале координат (рис. 3).

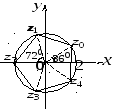
Рис. 3.

4.4. Функции комплексного переменного

Говорят, что в области определена функция, если каждой точкепоставлено в соответствие одно (однозначная функция) или несколько (многозначная функция) значений.

Пусть и. Тогда зависимостьмежду комплексной функциейи комплексной переменнойможет быть описана с помощью двух действительных функцийидействительных переменныхи:,.

Таким образом, функцию можно записать в виде:

,

где – действительная часть;– мнимая часть.

Основные элементарные функции комплексного переменного

1. Показательная функция

где

.

Свойства показательной функции:

1. Непрерывна на всей комплексной плоскости;

2. Периодична с периодом 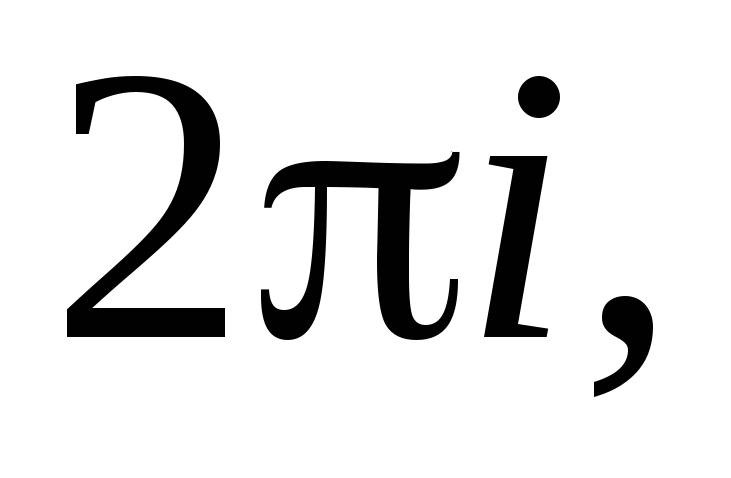т.е.;

3. Принимает все значения, кроме нуля, т.е. уравнение 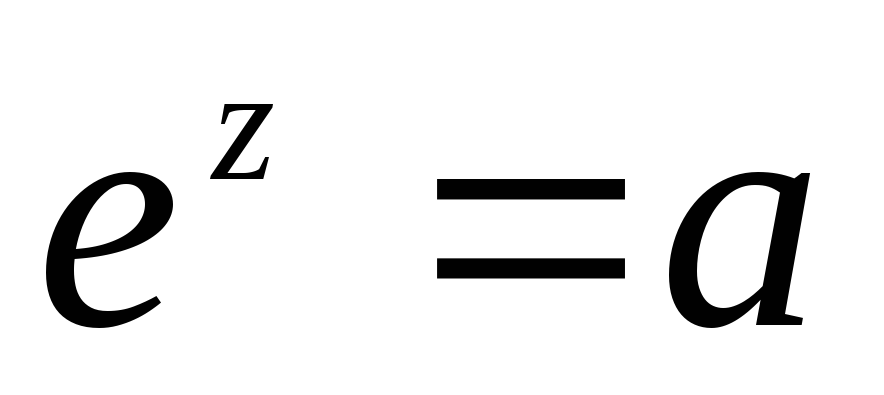разрешимо для любого;

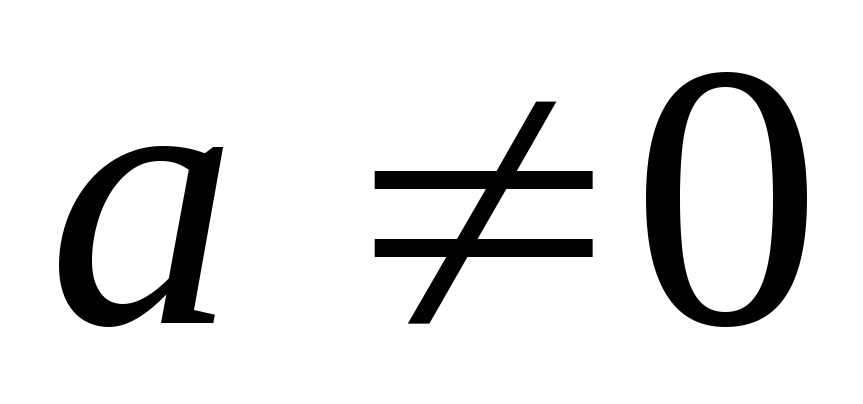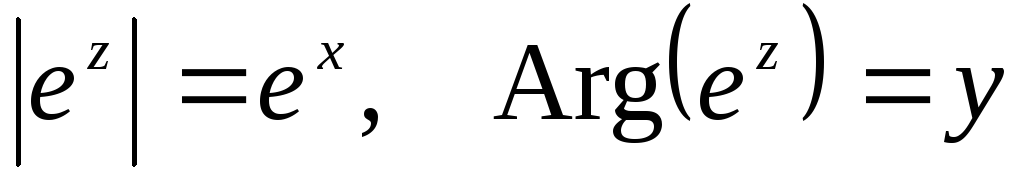4. ;

5.