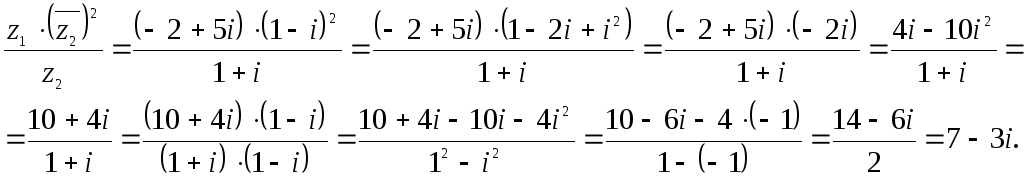4.1. Комплексные числа: определение, алгебра комплексных чисел, алгебраическая форма записи

Определение. Комплексным числом называется упорядоченная пара действительных чисел:

Например,

Определение. Два комплексных числа иназываются равными, еслии.

Определение. Суммой комплексных чисел иназывается число, определяемое равенством:

Определение. Произведением комплексных чисел иназывается число, определяемое равенством:

Легко проверить, что операции сложения и умножения комплексных чисел обладают свойствами:

1. Коммутативности:

2. Ассоциативности:

3. Дистрибутивности сложения относительно умножения:

4. Операции сложения и умножения над комплексными числами вида :

совпадают с соответствующими операциями над действительными числами и. Поэтому комплексные числа видаотождествляют с действительными числами:т.е. совокупность всех действительных чисел является частью совокупности комплексных чисел.

Среди комплексных чисел особую роль играет число , так какт.е. квадрат этого числа равен −1. Поэтому это число имеет особое обозначение:и его называютмнимой единицей:

Теперь всякое комплексное число мы можем записать в виде:

Итак, –алгебраическая форма записи комплексного числа

В этом случае называют действительной частью комплексного числаи символически обозначают:

называют мнимой частью комплексного числа и символически обозначают:

.

Определение. Число называют модулем комплексного числаи символически обозначают, т.е.

.

Определение. Комплексное число называется сопряжённым с комплексным числоми обозначается символом, т.е.

и – пара комплексно-сопряжённых чисел.

Легко убедиться, что . Действительно,

Используя введённые выше операции сложения и умножения комплексных чисел, можно определить операции вычитания и деления комплексных чисел.

Определение. Разностью комплексных чисел иназывается такое число, чтоОчевидно, что вычитание всегда выполнимо и, притом, единственным образом:

Определение. Частным двух комплексных чисел иназывается такое число, что.

Для выполнения операции деления достаточно домножить числитель и знаменатель на , т.е. на число сопряжённое знаменателю, тогда

т.е. деление на комплексное число (не равное нулю) выполнимо и единственно.

Замечание. Введённые правила выполнения арифметических действий над комплексными числами таковы, что если комплексные числа записаны в алгебраической форме, то все действия можно выполнять точно также, как и с действительными числами, помня только, что , и для выполнения деления необходимо числитель и знаменатель умножить на число, сопряжённое знаменателю.

Пример 1. Найти если,.

Решение. Чтобы выполнить указанные действия, запишем заданные комплексные числа ив алгебраической форме:

Тогда имеем:

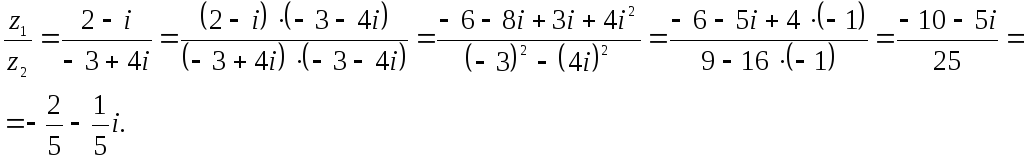Пример 2. Найти если

Решение. -это действительная часть комплексного числа .Имеем:

–это мнимая часть комплексного числа . Имеем: