2. Контрольная работа № 7. Задания

1. Проверить, является ли заданная функция решением данного дифференциального уравнения (табл. 1).

2. Определить типы дифференциальных уравнений первого порядка и решить их (табл. 2).

3. Решить задачу Коши для данного дифференциального уравнения первого порядка (табл. 3).

4. Найти общий интеграл дифференциального уравнения высшего порядка (табл. 4).

5. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами методом неопределённых коэффициентов (табл. 5).

2.1. Пример выполнения контрольной работы № 7. Вариант № 0

Задание 1. Проверить, является ли функция решением дифференциального уравнения

Решение. Найдем производную данной функции:

.

Подставляя ив данное уравнение, получаем верное равенство

Следовательно, функция является решением данного уравнения.

Задание 2. Определить типы дифференциальных уравнений и решить их:

а) ;

б) ;

в)

Решение. а) Выразим из уравнения производную :

.

Это уравнение вида , т.е. уравнение с разделяющимися переменными.

Имеем:

.

Разделяем переменные:

.

Интегрируем обе части последнего равенства:

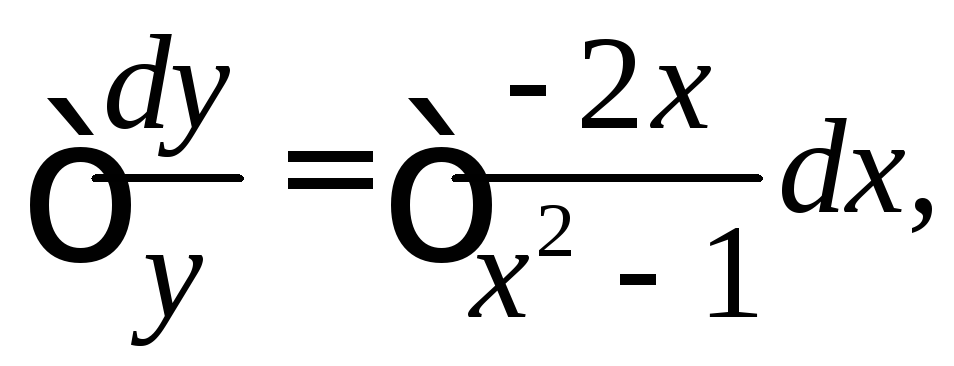
отсюда

–общее решение данного дифференциального уравнения.

При делении на мы могли потерять решение, однако оно входит в запись общего решения при

Ответ: .

б) . Разделив числитель и знаменатель правой части заданного уравнения на, получим уравнение:

Это однородное уравнение вида . Сделаем подстановку, где– новая неизвестная функция. Тогдаи уравнение приводится к виду

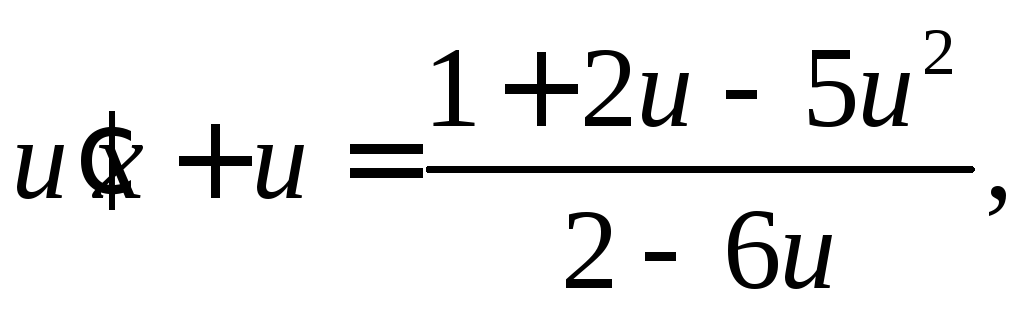
т.е. к уравнению с разделяющимися переменными.

Разделяем переменные:

Интегрируя обе части, получаем:

.

Заменяя на, получаем общий интеграл заданного уравнения

Ответ:

в) Видим, что это уравнение не является уравнением с разделяющимися переменными (переменные не разделить), не является ни однородным, ни линейным, ни уравнением Бернулли. Проверим условие. Имеем:

.

;

.

Таким образом, и уравнение является уравнением в полных дифференциалах, тогда

, поэтому

Продифференцируем найденную функцию по переменной:

.

Учитывая, что , получим уравнение, из которого найдём функцию:

,

Таким образом, Общий интеграл исходного дифференциального уравнения

Ответ:

Задание 3. Решить задачу Коши

Решение. Данное уравнение линейное, найдём его общее решение методом Бернулли. Сделаем подстановку

Подставим выражения для ив заданное уравнение:

. (*)

Найдём функцию как частное решение уравненияЭто уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем:

,

Подставляя найденную функцию в уравнение (*), получим второе дифференциальное уравнение с разделяющимися переменными, из которого найдём функцию:

.

Учитывая, что , получим общее решение исходного уравнения

.

Решим задачу Коши, т.е. найдём частное решение, удовлетворяющее заданному начальному условию т.е.при:

,

Таким образом, искомое частное решение есть или

Ответ:

Задание 4. Найти общий интеграл дифференциального уравнения высшего порядка: .

Решение. Это дифференциальное уравнение второго порядка вида , не содержащие явно искомой функции. Сделаем подстановку, тогда. Подставляя эти выражения в исходное уравнение, получаем:

,

т.е. получаем уравнение с разделяющимися переменными.

Разделяя переменные и интегрируя, имеем:

Учитывая, что , получаем:. Интегрируя, получим общее решение:

.

Ответ: .

Задание 5. Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами методом неопределённых коэффициентов:

Решение. Найдём сначала общее решение соответствующего однородного уравнения Для этого составим характеристическое уравнениеи найдём его корниОбщее решение однородного уравнения будет

Правую часть неоднородного уравнения запишем в виде суммы двух функций и, для которых частное решение можно искать методом неопределённых коэффициентов.

Частное решение, соответствующее правой части будем искать в виде:

.

Характеристическое число функции равно, поэтому, так какявляется корнем характеристического уравнения кратности 1, тогда

.

Имеем:

;

Подставляя эти выражения в неоднородное уравнение (с правой частью ) и сокращая на, получим:

, или

Приравниваем коэффициенты при одинаковых степенях и находим:

отсюда

Таким образом,

Частное решение, соответствующее правой части , запишем в виде:

.

Характеристическое число функции равно, поэтому, так какне является корнем характеристического уравнения, тогда

.

Имеем:

; .

Подставляя эти выражения в неоднородное уравнение (с правой частью ), получим:

, или

Приравниваем коэффициенты при одинаковых функциях слева и справа, получим:

отсюда

Таким образом, .

Следовательно, общее решение исходного дифференциального уравнения есть , или

Ответ: