1.5. Уравнения Бернулли

Определение. Уравнением Бернулли называется дифференциальное уравнение первого порядка вида

, (10)

где (приуравнение (10) является линейным, а при– уравнением с разделяющимися переменными).

Так же как и линейное уравнение, уравнение Бернулли можно проинтегрировать с помощью подстановки или свести к линейному уравнению с помощью подстановки.

Пример 10. Решить уравнение .

Решение. Это уравнение Бернулли с . Решим это уравнение методом Бернулли. Полагая, получаем:

,

. (11)

Функцию выбираем так, чтобы– это уравнение с разделяющимися переменными. Имеем:

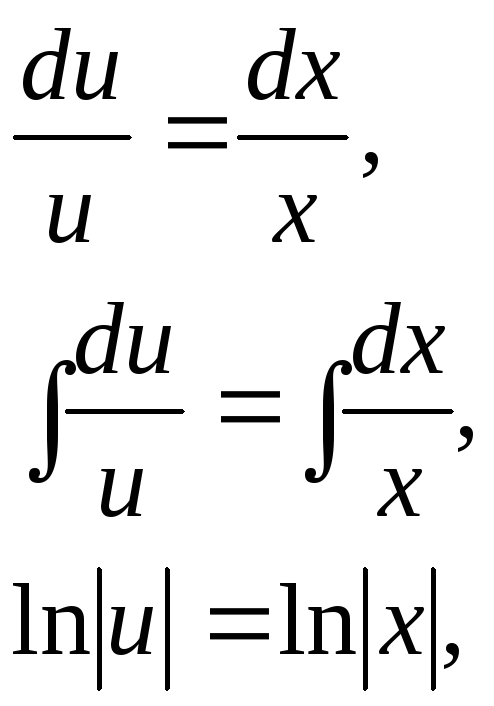
отсюда – некоторое частное решение.

Подставим найденную функцию в уравнение (11), получим:

, или

– это уравнение с разделяющимися переменными относительно функции

Разделяя переменные и интегрируя, получим:

,

, или

.

Учитывая, что , получим общий интеграл заданного дифференциального уравнения:

.

1.6. Уравнения в полных дифференциалах

Определение. Дифференциальное уравнение первого порядка вида

(12)

называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции , т.е.

,

где .

Для того чтобы уравнение (12) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие

.

Если уравнение (12) есть уравнение в полных дифференциалах, то оно может быть записано в виде

.

Общий интеграл этого уравнения , где– произвольная постоянная.

Функция может быть найдена следующим образом. Интегрируя равенство

по при фиксированноми, замечая, что произвольная постоянная в этом случае может зависеть от, имеем

(играет роль константы в неопределённом интеграле).

Чтобы найти функцию , воспользуемся вторым уравнением. Для этого продифференцируем найденную функциюпо переменной:

.

Отметим, что в получаемом на этом этапе решения дифференциальном уравнении не должно остаться членов, содержащих . Решив это уравнение, найдём функциюи тем самым общий интеграл исходного уравнения

.

Пример 11. Найти общий интеграл уравнения

.

Решение. Здесь

Следовательно, левая часть уравнения есть полный дифференциал некоторой функции , т.е.

.

Проинтегрируем первое равенство по :

.

Продифференцируем функцию по:

.

Используя второе равенство , получаем уравнение

,

откуда находим:

,

.

Тогда .

Таким образом, общий интеграл исходного уравнения имеет вид:

.

1.7. Дифференциальные уравнения высших порядков: основные определения, теорема Коши

Определение. Дифференциальным уравнением n-го порядка называется уравнение вида

(13)

или

. (14)

Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:

1) – дифференциальное уравнение второго порядка;

2) – дифференциальное уравнение третьего порядка;

3) – общий вид дифференциального уравнения второго порядка.

Определение. Задачей Коши для дифференциального уравнения (14) называется задача отыскания решения , удовлетворяющего заданным начальным условиям

. (15)

Определение. Общим решением уравнения (13) или (14) называется такая функция , которая при любых допустимых значениях параметровявляется решением этого дифференциального уравнения и для любой задачи Коши с начальными условиями (15) найдутся постоянные, определяемые системой уравнений

Определение. Уравнение , определяющее общее решение как неявную функцию, называется общим интегралом дифференциального уравнения.

Теорема Коши (существования и единственности решения задачи Коши). Если дифференциальное уравнение (14) таково, что функция в некоторой областиизмерения свих аргументов непрерывна и имеет непрерывные частные производные, то для любой точкисуществует интервал, на котором существует и притом единственное решение этого уравнения, удовлетворяющее начальным условиям (15).