
- •Оглавление
- •Введение
- •1. Дифференциальные уравнения
- •1.1. Дифференциальные уравнения первого порядка: основные определения, задача Коши
- •1.2. Уравнения с разделяющимися переменными
- •1.3. Однородные уравнения и уравнения, приводящиеся к ним
- •1.3.1. Однородные уравнения
- •1.3.2. Уравнения, приводящиеся к однородным
- •1.4. Линейные уравнения
- •1.5. Уравнения Бернулли
- •1.6. Уравнения в полных дифференциалах
- •1.7. Дифференциальные уравнения высших порядков: основные определения, теорема Коши
- •1.8. Уравнения, допускающие понижение порядка
- •1.9. Линейные дифференциальные уравнения второго порядка
- •1.9.1. Линейные однородные дифференциальные уравнения (лоду) второго порядка с постоянными коэффициентами
- •1.9.2. Линейные неоднородные дифференциальные уравнения (лнду) второго порядка с постоянными коэффициентами
- •2. Контрольная работа № 7. Задания
- •2.1. Пример выполнения контрольной работы № 7. Вариант № 0
- •2.2. Варианты заданий контрольной работы № 7
1.9.1. Линейные однородные дифференциальные уравнения (лоду) второго порядка с постоянными коэффициентами
Рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
![]() (19)
(19)
где
![]() – постоянные коэффициенты (числа).
– постоянные коэффициенты (числа).
Квадратное уравнение
![]() (20)
(20)
называется
характеристическим
уравнением для
уравнения (19) и получается из уравнения
(19) путём замены производных
![]() на степени
на степени![]() .
.
Для составления
общего решения
![]() дифференциального уравнения (19) необходимо
найти корни
дифференциального уравнения (19) необходимо
найти корни![]() и
и![]() соответствующего характеристического
уравнения (20) и применить следующую
теорему:
соответствующего характеристического
уравнения (20) и применить следующую
теорему:
Теорема 5. Пусть
![]() и
и![]() – корни характеристического уравнения
для уравнения (19). Тогда общее решение
уравнения (19) находится по одной из
следующих формул:
– корни характеристического уравнения
для уравнения (19). Тогда общее решение
уравнения (19) находится по одной из
следующих формул:
Если
 и
и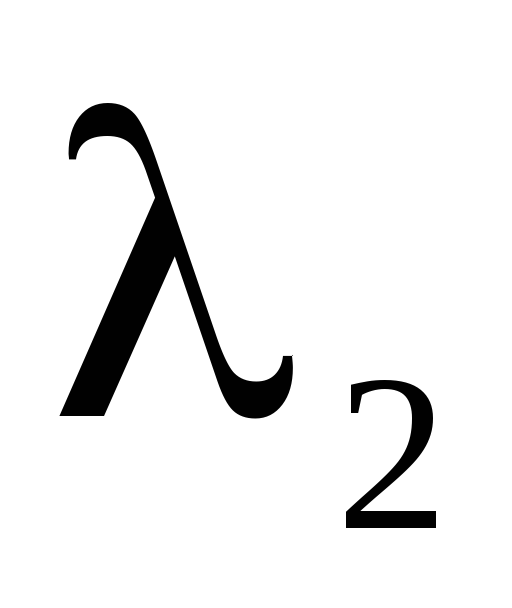 –
действительные и
–
действительные и
 ,
то
,
то
![]() ;
;
Если
 и
и –
действительные и
–
действительные и
 ,
то
,
то
![]() ;
;
Если
 – комплексно-сопряжённые корни
– комплексно-сопряжённые корни ,
то
,
то
![]()
Пример 17.
Найти общее решение уравнения
![]() .
.
Решение. Составляем характеристическое уравнение:
![]() .
.
Вычисляем дискриминант и корни квадратного уравнения:
![]()
![]()
![]() .
.
Запишем фундаментальную
систему решений:
![]() .
Следовательно, общее решение имеет вид:
.
Следовательно, общее решение имеет вид:
![]() .
.
Пример 18.
Найти общее решение уравнения
![]() .
.
Решение. Составляем характеристическое уравнение:
![]() .
.
Находим дискриминант и корни квадратного уравнения:
![]()
![]()
![]()
Следовательно,
функции
![]() составляют ФСР, а общее решение имеет
вид:
составляют ФСР, а общее решение имеет
вид:
![]() .
.
Пример 19. Найти
общее решение уравнения
![]() .
.
Решение. Составляем
характеристическое
уравнение:
![]() .
.
Находим дискриминант и корни квадратного уравнения:
![]()
![]()
![]()
Запишем
фундаментальную систему решений:
![]() .
Следовательно, общее решение имеет вид:
.
Следовательно, общее решение имеет вид:
![]() .
.
1.9.2. Линейные неоднородные дифференциальные уравнения (лнду) второго порядка с постоянными коэффициентами
Поскольку общее
решение
![]() линейного однородного уравнения (19)
легко находится по теореме 5, то в силу
теоремы 4 для нахождения общего решения
линейного неоднородного уравнения
линейного однородного уравнения (19)
легко находится по теореме 5, то в силу
теоремы 4 для нахождения общего решения
линейного неоднородного уравнения
![]() (21)
(21)
остаётся найти
какое-нибудь одно его частное решение
![]() .В тех случаях,
когда правая часть
.В тех случаях,
когда правая часть
![]() имеет специальный вид, частное решение
имеет специальный вид, частное решение![]() неоднородного
уравнения находится методом
неопределённых коэффициентов.
Этот метод называется также методом
подбора частного решения неоднородного
уравнения по специальному виду правой
части.
неоднородного
уравнения находится методом
неопределённых коэффициентов.
Этот метод называется также методом
подбора частного решения неоднородного
уравнения по специальному виду правой
части.
Специальным
видом функции
![]() называется следующий вид:
называется следующий вид:
![]() ,
,
где
![]() и
и![]() – многочлены степени
– многочлены степени![]() и
и![]() соответственно,
соответственно,
или
в частном случае (когда
![]() )
)
![]() .
.
Число
![]() называетсяхарактеристическим
числом функции
называетсяхарактеристическим
числом функции
![]() .
.
Если правая часть
уравнения (21) имеет такой вид, то частное
решение ![]() удобно искать
точно в таком же виде, в каком представлена
функция
удобно искать
точно в таком же виде, в каком представлена
функция
![]() ,
только вместо известных коэффициентов
в многочленах будут стоять неопределённые
коэффициенты, которые находятся при
подстановке построенной функции в
дифференциальное уравнение, т.е.
,
только вместо известных коэффициентов
в многочленах будут стоять неопределённые
коэффициенты, которые находятся при
подстановке построенной функции в
дифференциальное уравнение, т.е.
![]() .
.
Здесь
![]() – наибольшая из степеней
– наибольшая из степеней![]() и
и![]() ;
;![]() и
и![]() – многочлены степени
– многочлены степени![]() с неопределёнными коэффициентами.
с неопределёнными коэффициентами.
Если характеристическое
число
![]() не является корнем характеристического
уравнения (20), то
не является корнем характеристического
уравнения (20), то![]() Если
Если![]() есть корень характеристического
уравнения (20) кратности
есть корень характеристического
уравнения (20) кратности![]() ,
то
,
то![]()
![]() .
.
Так как предполагается, что данная функция есть решение дифференциального уравнения (21), то при подстановке этой функции в данное уравнение мы получим тождество, поэтому можно приравнивать коэффициенты при одинаковых линейно независимых функциях слева и справа. Это даёт систему уравнений для нахождения всех неопределённых коэффициентов.
Теорема 6. Если
![]() и
и![]() – частные решения
соответственно уравнений
– частные решения
соответственно уравнений
![]()
и
![]() ,
,
то
функция ![]() – частное решение уравнения
– частное решение уравнения
![]() .
.
Пример 20.
Найти решение уравнения
![]() ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям![]() .
.
Решение.
Характеристическое уравнение
![]() имеет корни
имеет корни![]() .
Общее решение соответствующего
однородного уравнения
.
Общее решение соответствующего
однородного уравнения
![]() .
.
Частное решение
![]() данного неоднородного уравнения будем
искать в виде
данного неоднородного уравнения будем
искать в виде ![]() ,
где
,
где ![]() – частное решение
уравнения
– частное решение
уравнения
![]() ,
(22) а
,
(22) а ![]() – частное решение уравнения
– частное решение уравнения
![]() . (23)
. (23)
1) Правая часть
уравнения (22) имеет вид:
![]() .
.
![]() –характеристическое
число функции
–характеристическое
число функции
![]() .
.
Частное решение
уравнения (22) будем искать в виде
![]() .
Так как
.
Так как![]() не является корнем характеристического
уравнения, то
не является корнем характеристического
уравнения, то![]() ,
т.е.
,
т.е.![]() Подставляя
Подставляя![]() в уравнение (22),
будем иметь
в уравнение (22),
будем иметь
![]() ,
,
откуда находим
![]() .
.
Таким образом,
![]() .
.
2) Правая часть
уравнения (23) имеет вид:
![]() .
.
![]() –характеристическое
число функции
–характеристическое
число функции
![]() .
.
Частное решение
уравнения (23) будем искать в виде
![]() .
Так как
.
Так как![]() не является корнем характеристического
уравнения, то
не является корнем характеристического
уравнения, то![]() ,
т.е.
,
т.е.![]() .
.
Для определения
неизвестного коэффициента
![]() имеем уравнение
имеем уравнение
![]() ,
,
откуда
![]() .
Тогда
.
Тогда![]() .
.
Следовательно, ![]() и общее решение
исходного уравнения
и общее решение
исходного уравнения
![]() .
.
Выделим теперь из
общего решения частное, удовлетворяющее
начальным условиям. Для этого
продифференцируем найденное
![]() :
:
![]() .
.
Используя начальные
условия
![]() при
при![]() ,
получим систему
,
получим систему
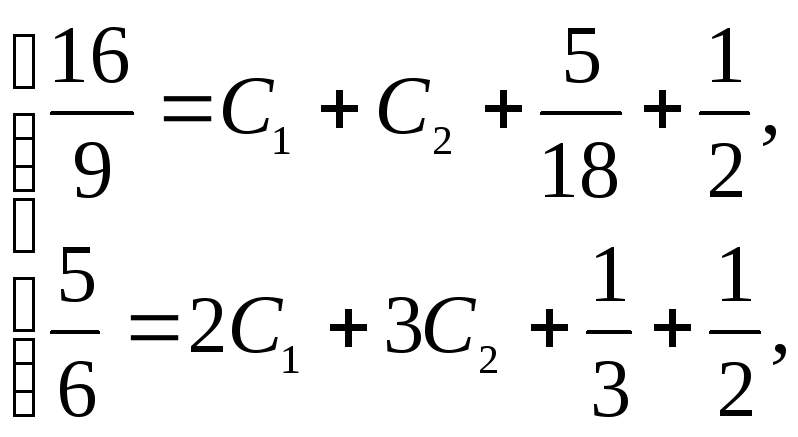
из которой находим:
![]() .
.
Искомое частное решение есть
![]() .
.
