1.3.2. Уравнения, приводящиеся к однородным

Рассмотрим дифференциальное уравнения вида

, (5)

где – постоянные, а – непрерывная функция своего аргумента . Если, то уравнение (5) является однородным и интегрируется, как указано в п. 1.3.1.

Если хотя бы одно из чисел отлично от нуля, то следует различать два случая:

1) Определитель . Вводя новые переменные, где – решение системы

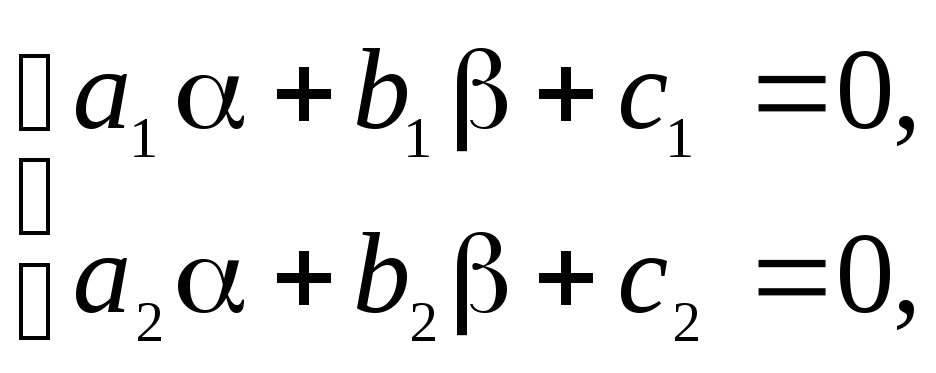
получим однородное уравнение.

2) Определитель . Подстановкапозволяет привести уравнение (5) к уравнению с разделяющимися переменными.

Пример 6. Решить уравнение .

Решение. Уравнение принадлежит к первому типу, поскольку

и .

Находим решение системы

Производим в исходном уравнении замену переменных, полагая . Тогда.

Уравнение преобразуется к виду

,

, или

.

В полученном однородном уравнении положим , откуда. Подставляя в последнее уравнение и преобразуя, придём к уравнению с разделяющимися переменными:

,

, или

.

Разделяем переменные:

.

Интегрируя, получим:

,

,

или после замены :

_.

Возвращаясь к переменным и, после элементарных преобразований найдём общий интеграл исходного уравнения

.

Пример 7. Решить уравнение .

Решение. Уравнение принадлежит ко второму типу, поскольку

.

Положим поэтому ,. Данное уравнение примет вид:

, или

.

Разделяя переменные и интегрируя, получим:

.

Возвращаясь к исходным переменным , получим окончательный ответ

.

1.4. Линейные уравнения

Определение. Дифференциальное уравнение первого порядка называется линейным, если оно содержит ив первой степени, т.е. имеет вид:

(6)

При уравнение (6) примет вид:

и называется линейным однородным. Оно является уравнением с разделяющимися переменными, а его общее решение имеет вид

,

где – произвольная постоянная, а– одна из первообразных функции.

Интегрирование линейного неоднородного уравнения (6) можно провести методом Бернулли.

Положим , тогда. Подставляя выражения дляив уравнение (6), получим:

.

Перенесём слагаемое в левую часть и сгруппируем с, выносяв качестве общего множителя:

. (7)

Согласно методу Бернулли функцию выбирают так, чтобы. Интегрируем уравнение с разделяющимися переменными:

и выбираем какое-либо его частное решение . Подставляя найденную функциюв уравнение (7), получаем уравнение с разделяющимися переменными относительно функции:

,

, тогда

,

т.е. находим общее решение этого уравнения .

Учитывая, что , получаем общее решение уравнения (6):

.

Пример 8. Найти общее решение уравнения .

Решение. Данное уравнение является линейным неоднородным.

Решим это уравнение методом Бернулли. Сделаем подстановку: . Имеем:

,

. (8)

Функцию выберем так, чтобы

, отсюда

.

Интегрируя обе части последнего равенства, получаем:

,

.

Подставим найденную функцию в уравнение (8), получим:

,

.

Вспоминая, что окончательно получаем общее решение данного дифференциального уравнения:

.

Пример 9. Найти частное решение уравнения , удовлетворяющее начальному условию

Решение. Относительно это уравнение не является линейным. Перепишем уравнение в виде

.

Это уравнение линейно относительно функции и её производной:

.

Решим его методом Бернулли: . Имеем:

,

. (9)

Решаем уравнение с разделяющимися переменными и находим его частное решение:.

Подставим найденную функцию в равенство (9), получим:

.

Учитывая, что получим общее решение уравнения

.

Найдём частное решение, используя заданное начальное условие , т.е.:

.

Тогда частное решение имеет вид: