3.2 Метод Зейделя

Деяка модифікація методу простої ітерації. Основна ідея в тому, що при обчисленні -го наближення невідомоївраховуються уже обчислені ранішенаближення невідомих, тобто виконуютьсяпослідовні ітерації. Схема методу Зейделя для системи (3.2):

Умова закінчення ітерацій .

Вказана вище теорема збіжності для простих ітерацій залишається вірною і для ітерацій за методом Зейделя.

Цей метод має кращу збіжність, ніж метод простих ітерацій, але приводить до більш об’ємних обчислень. Процес Зейделя може бути збіжним навіть у тому випадку, коли процес ітерацій розбіжний. Можливі випадки, коли метод Зейделя збігається і повільніше процесу простої ітерації, і навіть розбіжний за Зейделем.

Приклад. Знайти корені системи

які розташовані у І квадранті методом Зейделя з точністю 0,001.

Перетворення системи до вигляду зручного для ітерацій, та пошук початкового наближення приведені вище у розділі 3.1. Схема методу:

Отримані результати за методом Зейделя:

.

При цьому:

3.3 Метод Ньютона

Розглянемо систему рівнянь (3.1), і нехай (х) мають неперервні похідні першого порядку. Нехай також відоме -те наближення кореня х*.

Тоді (3.1) можна переписати у вигляді

f(х+х)= 0, де ∆х = х^*– х.

Для визначення похибки ∆х розкладемо функцію f(х) в ряд Тейлора й обмежимося першими диференціалами, тобто лінеаризуємо функцію:

Врахуємо (3.1) і перейдемо до векторного вигляду запису:

де J(x) – матриця Якобі (якобіан) системи (3.1):

Звідси випливає спосіб обчислення чергового (+ 1)-го набли­ження:

хx(J(x))f(x); (3.7)

У достатньо малому околі розв'язку х* ітераційний процес (3.7) є збіжним, якщо існує обернена матриця J (х), а для цього необхідно, щоб

Теорема 1. Достатні умови збіжності методу Ньютона.

Нехай функція є неперервно диференційованою у відкритій множинііснуєітакі, що- відкритий окіл радіусаr з центром у точці, тобто , а також існує, причому, інеперервна по Ліпшицю з константою ЛіпшицяL тобто для довільнихпослідовність, яка породжується (3.7), збігається до і задовольняє нерівності: .

Зауваження 1. Ітераційний процес (3.7) має квадратичну швидкість збіжності. Якщо початкове наближення х⁽⁰⁾ вибране вдало, то процес (3.7) дає задовільну точність за три-п'ять ітерацій.

Зауваження 2. Якщо на всіх ітераціях використовувати за­мість J(х) стале, обчислене для х⁽⁰⁾ значення якобіану J(х⁽⁰⁾), то отримаємо модифікований метод Ньютона:

Швидкість збіжності у цьому випадку стане лінійною і, відпо­відно, збільшиться кількість необхідних для досягнення заданої точності ітерацій.

Недоліки метода:

• необхідність задавати досить "гарне" початкове наближення;

• відсутність глобальної збіжності для багатьох задач;

• необхідність обчислення матриці Якобі на кожній ітерації;

• необхідність розв’язування на кожній ітерації системи лінійних рівнянь, яка може бути погано зумовленою.

Розглянемо метод Ньютона для системи двох рівнянь.

Запишемо систему (3.1) у вигляді:

(3.8)

Тоді згідно з методом Ньютона послідовні наближення обчис­лимо за формулами

а матриця Якобі має вигляд

Початкові наближення можна визначити, наприклад, графічно.

Метод Ньютона ефективний лише тоді, коли вектор початко­вих наближень х⁽⁰⁾ достатньо близький до розв'язку системи (3.1) х*.

Приклад 1. Перевірити чи ітераційний процес буде збіжний для системи не­лінійних рівнянь

Графічно можна знайти грубе наближення значення коренів Обчислимо якобіан

Якобіан відмінний від нуля, тому ітераційний процес збіжний.

Приклад 2. Методом Ньютона знайти розв’язок системи

який знаходиться у І квадранті з точністю .

Початкове наближення .

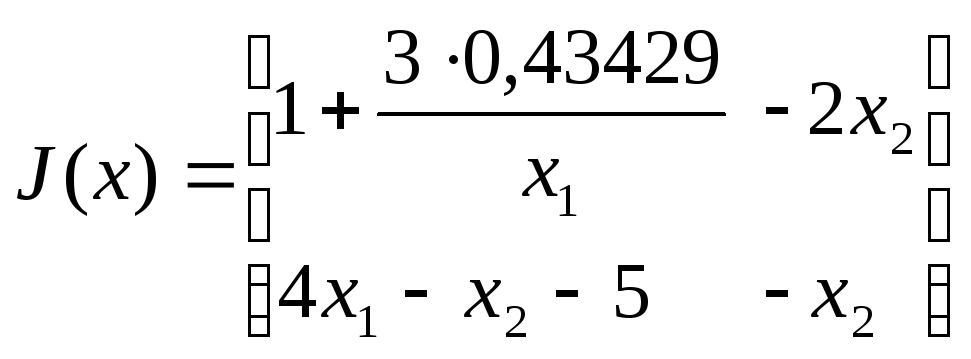–матриця Якобі. .

За формулою (3.7):

Так як , то шукаємо друге наближення:Звідки:. Аналогічно попередньому отримаємо:

.

Висновок: за методом простих ітерацій ( приклад 2 розділ 3.1 ) точність досягається за 4 ітерації, а за методом Ньютона – за 3.

Відповідь:

Приклад 3. Знайти розв’язок системи методом Ньютона з точністю .

Початкові наближення . Матриця Якобі

. В точці

.

Так як , то знаходимо:

звідси:

<

Відповідь: .