
- •Методичні вказівки до практичних занять
- •Обчислювальна математика
- •2010 Зміст
- •Урахування похибок
- •1.1 Основні джерела похибок
- •1.2 Основні поняття
- •1.3 Правила обчислення похибок
- •1.4 Деякі правила обчислення максимальних граничних похибок
- •1.5 Приклади
- •1.6 Задачі
- •Методи розв'язування нелінійних рівнянь
- •2.1 Відокремлення коренів
- •2.2 Метод половинного поділу (бісекцій або діхотомії)
- •2.3 Метод січних (хорд, пропорційних частин)
- •2.4 Метод Ньютона (дотичних, лінеаризації)
- •2.4.1 Модифікований метод Ньютона
- •2.4.2 Метод Ньютона-Бройдена
- •2.5 Метод хорд та дотичних (комбінований метод)
- •2.6 Метод простих ітерацій
- •Методи розв'язування систем нелінійних рівнянь
- •3.1 Метод простих ітерацій
- •3.2 Метод Зейделя
- •3.3 Метод Ньютона
- •3.4 Модифікований метод Ньютона
- •Розв’язування систем лінійних алгебраїчних рівнянь (слар)
- •4.1 Метод ітерації
- •4.2 Зведення слар до вигляду, який придатний до застосування методу ітерації.
- •4.3 Метод Зейделя
- •4.4 Метод релаксації
- •4.5 Метод прогонки
- •4.6 Методика розв’язування задачі
- •5. Наближення функцій
- •5.1 Інтерполяція
- •5.2 Інтерполяційна формула Лагранжа
- •5.3 Оцінка похибки інтерполяційної формули Лагранжа
- •5.4 Збіжність функціонального інтерполяційного процесу неперервних функцій
- •5.5 Методика розв’язування задачі лінійної інтерполяції
- •5.6 Методика розв’язування задачі параболічної інтерполяції
- •5.7 Поліноми Чебишева
- •5.8 Інші методи інтерполяції. Інтерполяційний многочлен Ньютона
- •5.9 Методи інтегрально-диференціальної інтерполяції
- •5.10 Методи інтегрального згладжування
- •5.11 Метод найменших квадратів
- •5.12 Особливості мнк
- •5.13 Метод найкращого інтегрального наближення
- •5.14 Методи інтерполяції та згладжування на основі сплайнів
- •5.15 Інтерполяційні диференціальні кубічні сплайни
- •Список використаних джерел
5.7 Поліноми Чебишева
Похибка
![]() формули Лагранжа залежать від вигляду
функції
формули Лагранжа залежать від вигляду
функції![]() ,
яка не піддається регулюванню, і добутку
,
яка не піддається регулюванню, і добутку![]() ,
який залежить від вузлів інтерполяції.
При невдалому розташуванні вузлів
інтерполяції верхня межа модуля похибки
,
який залежить від вузлів інтерполяції.
При невдалому розташуванні вузлів
інтерполяції верхня межа модуля похибки![]() може бути дуже великою. Наприклад, якщо
взяти вузли біля одного з кінців відрізка,
то
може бути дуже великою. Наприклад, якщо
взяти вузли біля одного з кінців відрізка,
то![]() буде дуже великою. Виникає задача про
найбільш раціональний вибір вузлів
інтерполяції
буде дуже великою. Виникає задача про
найбільш раціональний вибір вузлів
інтерполяції![]() при заданій їх кількостіп,
щоб
при заданій їх кількостіп,
щоб
![]() мала найменше значення максимуму на
відрізку
мала найменше значення максимуму на
відрізку![]() .
.
Цю задачу розв’язав П.Л. Чебишева, який довів, що найкращий вибір вузлів інтерполяції задається формулою:
![]() ,
де
,
де
![]() -
нулі полінома Чебишева.
-
нулі полінома Чебишева.![]() .
.
Тоді:
![]() .
.
Вузли не рівновіддалені. Вони згущаються біля кінців відрізка.

Властивості поліномів Чебишева:
- функція
![]() -
поліномп
степеня;
-
поліномп
степеня;
- поліноми
Чебишева І роду ортогональні на відрізку
![]() з вагою
з вагою![]() :
: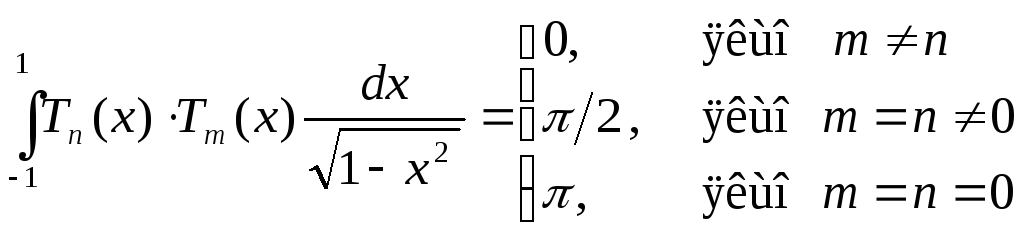 ;
;
- усі
корені
![]() знаходяться на інтервалі
знаходяться на інтервалі![]() ,
тобто вони усі дійсні і
,
тобто вони усі дійсні і![]() ;
;
-
максимальна значення
![]() на
на![]() дорівнює 1:
дорівнює 1:![]() ;
;
-
коефіцієнт при
![]() для
для![]() дорівнює
дорівнює![]() ;
;
- поліном
![]() парний при парномуп
і непарний при непарному п;
парний при парномуп
і непарний при непарному п;
- основні
рекурентні співвідношення для
![]() :
:
-
![]() задовольняє
диференціальному рівнянню:
задовольняє
диференціальному рівнянню:
![]()
- основна
властивість поліномів Чебишева: серед
усіх поліномів степеня п
поліном
![]() найменше відхиляється від 0.
найменше відхиляється від 0.
Таким
чином при інтерполяції по поліномам
Чебишева в якості базисних функцій
вибирають
![]() .
.
Приклади
поліномів:
![]()
5.8 Інші методи інтерполяції. Інтерполяційний многочлен Ньютона
Інколи зручніше при функціональній інтерполяції використовувати многочлени Ньютона, якими можна послідовно підвищувати степінь інтерполяції при додаванні чергових доданків. Такі несиметричні многочлени засновані на розділених і кінцевих різницях, які обчислюються по інтерпольованій сітковій функції ([1],[2]).
Розділені
різниці вводяться для функції
![]() ,
яка задана на нерівномірній сітці, а
скінчені різниці – на рівномірній
сітці.
,
яка задана на нерівномірній сітці, а
скінчені різниці – на рівномірній
сітці.
Розділена
різниця І порядку:
![]() .
.
Розділена
різниця ІІ порядку:
![]() .
.
Розділена
різниця
![]() -го
порядку:
-го
порядку:![]() .
.
Скінченна
різниця І порядку:
![]() .
.
Скінченна
різниця ІІ порядку:
![]() .
.
Скінченна
різниця
![]() -го
порядку:
-го
порядку:![]() ,
де
,
де![]() -
біноміальний коефіцієнт.
-
біноміальний коефіцієнт.
Для
гладких функцій
![]() і
і![]() при
при![]() .
.
Нехай
вихідна функція
![]() задана на нерівномірній сітці.
задана на нерівномірній сітці.![]() ,
тобто
,
тобто![]() .
Длякускового
способу маємо шаблон
.
Длякускового
способу маємо шаблон
![]() ,
тоді многочлен Ньютона
,
тоді многочлен Ньютона![]() -го
степеня:
-го
степеня:
![]() (5.6)
(5.6)
Глобальний
спосіб:
![]() ,
,![]() ,
тобто на сітці
,
тобто на сітці![]() .
.
Для
рівномірної сітки
![]() маємо для кускового способа:
маємо для кускового способа:
![]() (5.7)
(5.7)
![]() -
інтерполяційний багаточлен для
інтерполяції вперед (на початку таблиці)
або екстраполяції назад.
-
інтерполяційний багаточлен для
інтерполяції вперед (на початку таблиці)
або екстраполяції назад.
Залишковий член:
![]() (5.8)
(5.8)
де
![]() - деяке проміжне значеннях.
- деяке проміжне значеннях.
Якщо фазу інтерполяції визначити відносно кінцевої точки інтервала інтерполяції, то:
![]() (4)
(4)
При
![]() отримаємо розв’язок задачіглобальної
інтерполяції.
отримаємо розв’язок задачіглобальної
інтерполяції.
![]() -
многочлен для інтерполяції назад
-
многочлен для інтерполяції назад
![]() або екстраполяції вперед – другий
інтерполяційний многочлен Ньютона.
або екстраполяції вперед – другий
інтерполяційний многочлен Ньютона.
Залишковий
член записується у формі (5.8), де
![]() .
.
Зауваження:
Згідно з теоремою про єдиність розв’язку задачі інтерполяції многочлен Ньютона є тотожним до многочлену, коефіцієнти якого є розв’язком системи початкових умов
 або до многочлену Лагранжа, якщо вузли
інтерполяції та інтерпольована функція
однакові.
або до многочлену Лагранжа, якщо вузли
інтерполяції та інтерпольована функція
однакові.Для підвищення (зниження) точності інтерполяції многочленами Ньютона треба додати (відняти) відповідну кількість доданків. Це інколи спрощує алгоритм інтерполяції.
При інтерполяції по І або ІІ інтерполяційному многочленах Ньютона шаблони інтерполяції доцільно вибирати так, щоб точка х була якомога ближча до середини відрізка
 .
.Залишковий член (5.8) збігається із залишковим членом для многочлена Лагранжа.
Для гладких функцій при підвищенні порядку скінчених різниць виконується
 при
при
 ,тому
як тільки черговий доданок в розглянутих
многочленах стає менше заданої точності
обчислень, збільшення степеня
,тому
як тільки черговий доданок в розглянутих
многочленах стає менше заданої точності
обчислень, збільшення степеня
 треба припинити.
треба припинити.
Приклад
1.
Обчислити значення функції в точці
![]() ,
яка задана таблицею за допомогою
многочлена Ньютона 3 степеня:
,
яка задана таблицею за допомогою
многочлена Ньютона 3 степеня:
Таблиця 5.3
Таблиця значень f(x)
|
|
0 |
1 |
2 |
3 |
|
|
2 |
3 |
4 |
5 |
|
|
7 |
5 |
8 |
7 |
Побудуємо многочлен Ньютона, який виконується при довільному розташуванні вузлів. Тоді:
![]()
 .
.
![]()

Для І інтерполяційного многочлена Ньютона:

![]()

Для ІІ інтерполяційного многочлена Ньютона:

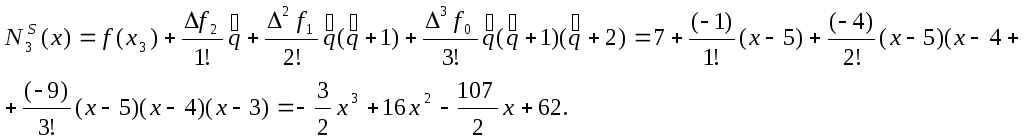
Звідси
![]() для
для![]() маємо
маємо![]() .
.
Приклад
2.
Нехай в прикладі 1 отриманий новий
результат
![]() .
Розташуємо його в кінці таблиці.
Розв’яжемо задачу з додатковим значенням
сіткової функції.
.
Розташуємо його в кінці таблиці.
Розв’яжемо задачу з додатковим значенням
сіткової функції.
Відповідно до (5.6) маємо:

Якщо
додати новий вузол спочатку таблиці,
то результат буде таким же
![]()
Приклад
3.
Для сіткової функції, яка задана таблицею
5.2, знайти лінійний і квадратичний
многочлени Ньютона, та на їх основі
обчислити
![]() .
.
Інтервал
інтерполяції
![]() .
.
![]() .
.
![]()
![]()
Порівнюючи
з результатами розділа 5.2 для многочленів
Лагранжа, маємо
![]() .
.
![]()
Точне
значення
![]() .
.
Приклад
4.
Знайти апріорну оцінку похибки лінійної
інтерполяції на відрізку
![]() .
.
Оцінимо
похідну
![]() чисельними диференціюванням. Для цього
знаходимо
чисельними диференціюванням. Для цього
знаходимо![]() .
Тоді
.
Тоді![]() .
.
Приклад
5.
Для сіткової функції, яка задана таблицею
5.3, побудувати інтерполяційні многочлени
1 і 2 степенів для знаходження значень
у точках
![]()
Для
 маємо шаблон
маємо шаблон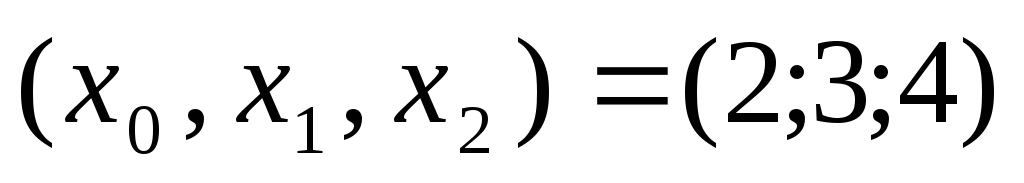 ,
тобто
,
тобто для квадратичної інтерполяції та шаблон
для квадратичної інтерполяції та шаблон ,
тобто
,
тобто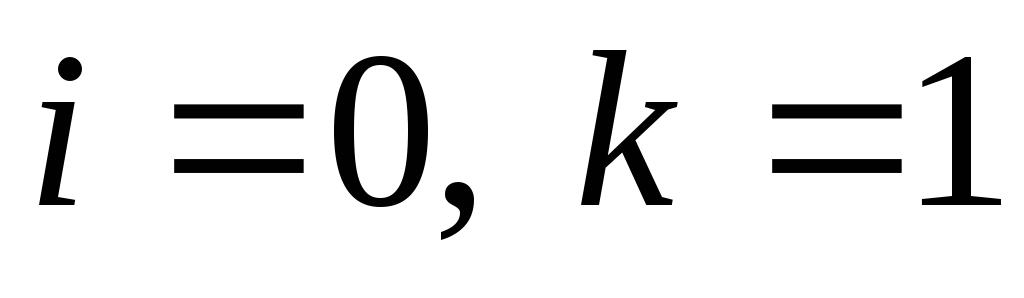 для лінійної інтерполяції. Тоді
для лінійної інтерполяції. Тоді .
.
![]()
![]() .
.
Для
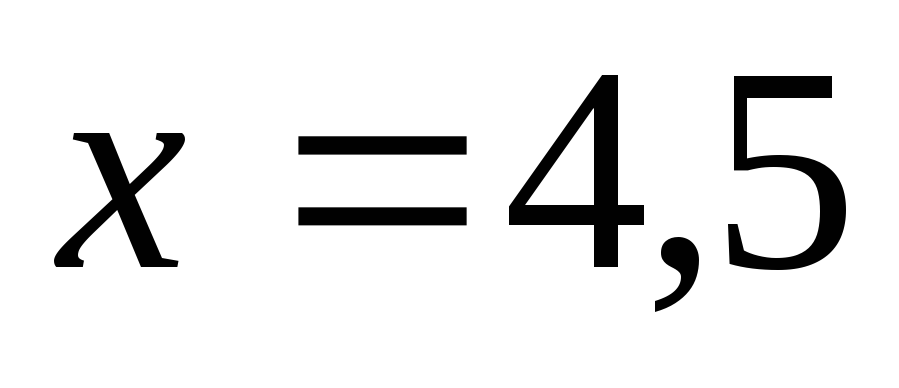 маємо шаблони
маємо шаблони або
або для квадратичної інтерполяції та
для квадратичної інтерполяції та або
або для лінійної інтерполяції. Тоді
для лінійної інтерполяції. Тоді .
.
![]() .
.
![]() .
.
Для
 можна використати
можна використати ;
; ,
тобто виконаємо екстраполяцію.
,
тобто виконаємо екстраполяцію.Для
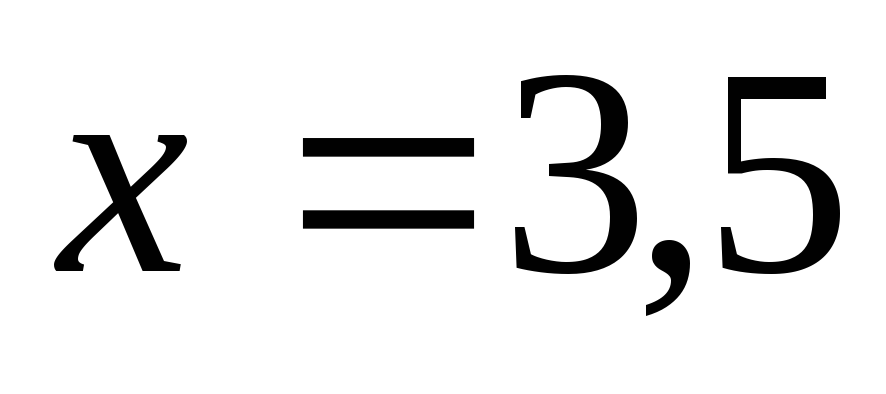 виберемо спочатку шаблон
виберемо спочатку шаблон або
або для квадратичної інтерполяції і
для квадратичної інтерполяції і або
або для лінійної інтерполяції. Тоді
для лінійної інтерполяції. Тоді .
.
![]() ;
;
![]() .
.
Виберемо
шаблон
![]() або
або![]() для квадратичної інтерполяції та
для квадратичної інтерполяції та![]() або
або![]() для лінійної інтерполяції
для лінійної інтерполяції![]() .
.
![]()
![]()
