
- •Методичні вказівки до практичних занять
- •Обчислювальна математика
- •2010 Зміст
- •Урахування похибок
- •1.1 Основні джерела похибок
- •1.2 Основні поняття
- •1.3 Правила обчислення похибок
- •1.4 Деякі правила обчислення максимальних граничних похибок
- •1.5 Приклади
- •1.6 Задачі
- •Методи розв'язування нелінійних рівнянь
- •2.1 Відокремлення коренів
- •2.2 Метод половинного поділу (бісекцій або діхотомії)
- •2.3 Метод січних (хорд, пропорційних частин)
- •2.4 Метод Ньютона (дотичних, лінеаризації)
- •2.4.1 Модифікований метод Ньютона
- •2.4.2 Метод Ньютона-Бройдена
- •2.5 Метод хорд та дотичних (комбінований метод)
- •2.6 Метод простих ітерацій
- •Методи розв'язування систем нелінійних рівнянь
- •3.1 Метод простих ітерацій
- •3.2 Метод Зейделя
- •3.3 Метод Ньютона
- •3.4 Модифікований метод Ньютона
- •Розв’язування систем лінійних алгебраїчних рівнянь (слар)
- •4.1 Метод ітерації
- •4.2 Зведення слар до вигляду, який придатний до застосування методу ітерації.
- •4.3 Метод Зейделя
- •4.4 Метод релаксації
- •4.5 Метод прогонки
- •4.6 Методика розв’язування задачі
- •5. Наближення функцій
- •5.1 Інтерполяція
- •5.2 Інтерполяційна формула Лагранжа
- •5.3 Оцінка похибки інтерполяційної формули Лагранжа
- •5.4 Збіжність функціонального інтерполяційного процесу неперервних функцій
- •5.5 Методика розв’язування задачі лінійної інтерполяції
- •5.6 Методика розв’язування задачі параболічної інтерполяції
- •5.7 Поліноми Чебишева
- •5.8 Інші методи інтерполяції. Інтерполяційний многочлен Ньютона
- •5.9 Методи інтегрально-диференціальної інтерполяції
- •5.10 Методи інтегрального згладжування
- •5.11 Метод найменших квадратів
- •5.12 Особливості мнк
- •5.13 Метод найкращого інтегрального наближення
- •5.14 Методи інтерполяції та згладжування на основі сплайнів
- •5.15 Інтерполяційні диференціальні кубічні сплайни
- •Список використаних джерел
5.11 Метод найменших квадратів
Нехай
у вузлах
![]() задані значення функції
задані значення функції![]() ,
де
,
де![]() .
Треба знайти коефіцієнти
.
Треба знайти коефіцієнти![]() ,
узагальненого многочлена
,
узагальненого многочлена
![]() (5.15)
(5.15)
де
![]() -
система базисних функцій, які забезпечують
мінімум:
-
система базисних функцій, які забезпечують
мінімум:
![]()
Необхідна
умова безумовного екстремуму:
![]() де
де![]() .
.
У результаті можна отримати:
 (5.16)
(5.16)
Система
(5.16) називається нормальною системою
МНК. Для лінійної апроксимації маємо:
![]() .
Система (5.16) набуває вигляду:
.
Система (5.16) набуває вигляду:

Звідси:
 ,
(5.17)
,
(5.17)
де
 -
середні значеннях
і у.
-
середні значеннях
і у.
Для
квадратичної апроксимації
![]() отримаємо:
отримаємо:
 . (5.18)
. (5.18)
Приклад 1. Визначити рівняння прямої за МНК, яка проходить найближче до таких точок:
-
х
1
1,5
2
2,5
3
3,5
у
0,29
0,81
1,26
1,85
2,5
3,01
За формулами (5.17) отримаємо:

Відповідь:
![]() .
.
Приклад 2. Визначити рівняння прямої за МНК, яка проходить найближче до таких точок:
-
х
2,8
2,2
3
3,5
3,2
3,7
4
4,8
6
5,4
5,2
5,4
6
9
у
6,7
6,9
7,2
7,3
8
8,8
9,1
9,8
10,6
10,7
11,1
11,8
12,1
12,4
Аналогічно попередньому отримаємо:
![]()
Відповідь:
![]() .
.
Приклад 3. Визначити рівняння прямої за МНК, яка проходить найближче до таких точок:
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
5,7 |
6,7 |
5,2 |
3,2 |
3,7 |
Відповідь:
![]() .
.
Приклад 4. Визначити рівняння прямої та параболи за МНК, які проходять найближче до таких точок:
|
х |
2 |
3 |
4 |
5 |
|
у |
7 |
5 |
8 |
7 |
За
формулами (5.17), (5.18) отримаємо
![]()
5.12 Особливості мнк
Метод інтерполяції – точковий метод, тому що потребує виконання точкових умов інтерполяції. МНК є інтерполяційним методом і не потребує точного виконання функціональних умов, вимагає відповідності
 і
і в середньому (за інтегралом або за
інтегральною сумою).
в середньому (за інтегралом або за
інтегральною сумою).Вихідна функція
 задана неточно, а з деякою похибкою,
суттєво більшою, ніж у методі інтерполяції.
Ця похибка зумовлена результатами
фізичного досліду.
задана неточно, а з деякою похибкою,
суттєво більшою, ніж у методі інтерполяції.
Ця похибка зумовлена результатами
фізичного досліду.Кількість точок
 ,
у яких задана вихідна функція, як
правило, значно більше степенят
многочлена
,
у яких задана вихідна функція, як
правило, значно більше степенят
многочлена
 .
Тому міжп
і т
немає відповідності, як це має місце в
методі інтерполяції.
.
Тому міжп
і т
немає відповідності, як це має місце в
методі інтерполяції.
Зауваження.
Якщо для функції, яка задана в
 точці, визначати многочлен степеня
точці, визначати многочлен степеня за МНК, то
за МНК, то збігається з інтерполяційним многочленом
і метод стає еквівалентним методу
інтерполяції з нульовою дисперсією.
збігається з інтерполяційним многочленом
і метод стає еквівалентним методу
інтерполяції з нульовою дисперсією.У кожному конкретному випадку може існувати "оптимальна" степінь т, яка залежить від конкретної поведінки функції, числа п і вигляду базисних функцій
 .
Нехай похибка задання вихідної функції
характеризується тільки одним значенням
.
Нехай похибка задання вихідної функції
характеризується тільки одним значенням (усі похибки однакові).
(усі похибки однакові).
Задаючи
деяке т,
визначають коефіцієнти
![]() ,
та середнє квадратичне відхилення
,
та середнє квадратичне відхилення![]() і порівнюють його з
і порівнюють його з![]() .
Можливі три випадки:
.
Можливі три випадки:
якщо
 ,
то апроксимація дуже груба, степіньт
недостатня, треба її збільшити;
,
то апроксимація дуже груба, степіньт
недостатня, треба її збільшити;якщо
 ,
то апроксимація фізично недостовірна,
степіньт
треба зменшити;
,
то апроксимація фізично недостовірна,
степіньт
треба зменшити;якщо
 ,
то степінь многочленат
є оптимальною.
,
то степінь многочленат
є оптимальною.
Система (2) при
 стає погано зумовленою і визначити
многочлен
стає погано зумовленою і визначити
многочлен практично неможливо. Необхідно замість
степеневих базисних функцій
використовувати, наприклад, поліноми
Чебишова або інші базисні функції.
практично неможливо. Необхідно замість
степеневих базисних функцій
використовувати, наприклад, поліноми
Чебишова або інші базисні функції.МНК реалізує найкраще в середньому наближення у всій області визначення функції
 і в деяких випадках не враховує локальних
властивостей функції
і в деяких випадках не враховує локальних
властивостей функції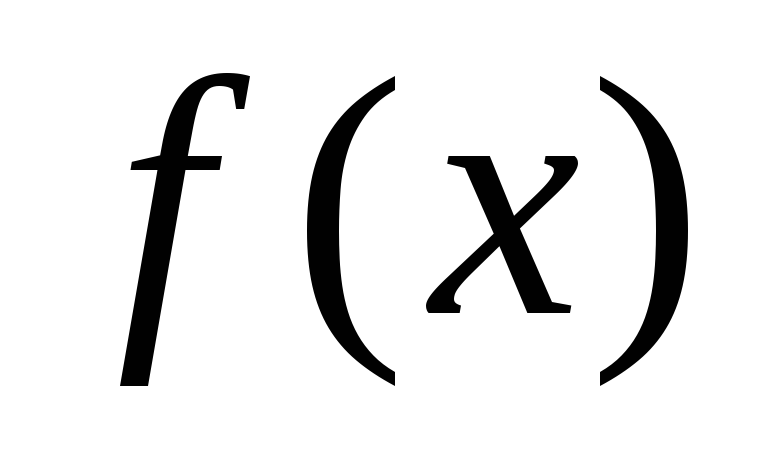 ,
наприклад, окремі піки функції.
,
наприклад, окремі піки функції.Реалізація МНК з використанням степеневих функцій пов’язана з розв’язуванням СЛАР відповідно до коефіцієнтів
 ,
причому при зміні степенят
усі коефіцієнти необхідно розраховувати
знову. Цей недолік усувається вибором
ортогональних базисних функцій
,
причому при зміні степенят
усі коефіцієнти необхідно розраховувати
знову. Цей недолік усувається вибором
ортогональних базисних функцій
 .
.
