
- •Методичні вказівки до практичних робіт
- •З дисципліни "Обчислювальна математика"
- •Для студентів заочного відділення кі Сум ду
- •Методи розв'язування нелінійних рівнянь
- •Метод половинного поділу (бісекцій або діхотомії)
- •Метод січних (хорд, пропорційних частин)
- •Метод Ньютона (дотичних)
- •Метод хорд та дотичних (комбінований метод)
- •Метод простих ітерацій
- •Методи розв'язування систем нелінійних рівнянь
- •Метод простих ітерацій
- •Метод Зейделя
- •Метод Ньютона
- •Метод прямокутників
- •Метод трапецій
- •Метод Сімпсона (парабол)
Методичні вказівки до практичних робіт
З дисципліни "Обчислювальна математика"
Для студентів заочного відділення кі Сум ду
Методи розв'язування нелінійних рівнянь
Якщо алгебраїчне та трансцендентне рівняння досить складні, то корені рідко вдається знайти точно. Окрім того, в деяких випадках коефіцієнти відомі лише приблизно, і тому задача про точне визначення коефіцієнтів рівняння не має сенсу. Тому важливе значення мають способи приблизного знаходження коренів рівняння та оцінка степені їх точності.
Нехай
задано неперервну функцію
![]() в деякому обмеженому або необмеженому
інтервалі
в деякому обмеженому або необмеженому
інтервалі![]() .
Необхідно знайти всі або деякі корені
рівняння
.
Необхідно знайти всі або деякі корені
рівняння
![]() (1)
(1)
Корінь
рівняння (1) – всяке значення
![]() ,
яке обертає
,
яке обертає![]() в нуль (тотожність (1)), тобто
в нуль (тотожність (1)), тобто![]() ,
або нуль функції
,
або нуль функції![]() .
.
Вважаємо, що (1) має тільки ізольовані корені. Ця задача передбачає два етапи розв'язування:
а)
відокремлення коренів, тобто виокремлення
достатньо малої області, що належить
до області допустимих значень функції
![]() ,
у
якій є один і тільки один корінь;
,
у
якій є один і тільки один корінь;
б) уточнення наближеного значення кореня до наперед заданої точності.
Для відокремлення дійсних коренів корисно знати кількість коренів, а також нижню і верхню межі їх розташування. Для цього використовується ряд теорем.
Теорема Больцано-Коші. Якщо неперервна функція
 на кінцях відрізка має різні за знаком
значення, тобто
на кінцях відрізка має різні за знаком
значення, тобто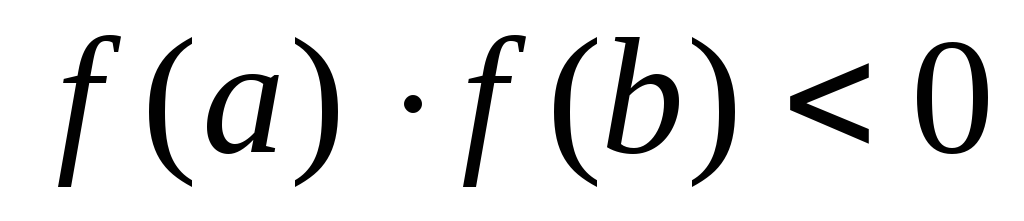 ,
то на цьому відрізку рівняння (1) має
хоча б один корінь. Якщо, крім цього,
існує
,
то на цьому відрізку рівняння (1) має
хоча б один корінь. Якщо, крім цього,
існує і
зберігає знак, тобто
і
зберігає знак, тобто
 або
або >0,
то корінь єдиний.
>0,
то корінь єдиний.Алгебраїчний багаточлен
![]() (2)
(2)
степеня
![]() має рівно
має рівно![]() коренів, дійсних або комплексних, при
умові, що кожний корінь підраховується
таку кількість разів, якій дорівнює
його кратність.
коренів, дійсних або комплексних, при
умові, що кожний корінь підраховується
таку кількість разів, якій дорівнює
його кратність.
Якщо
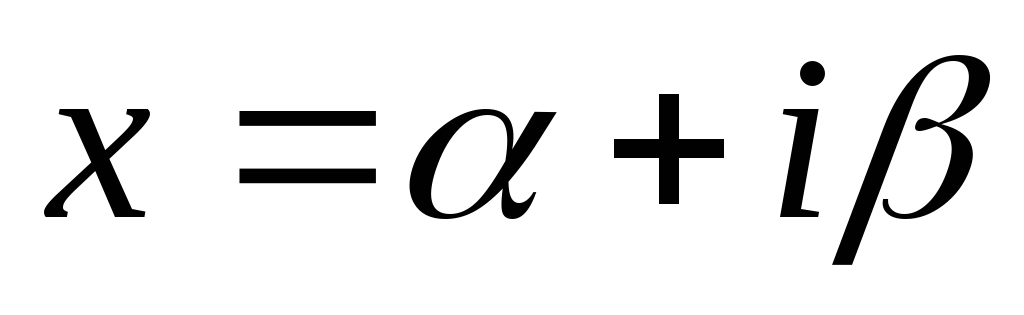 - корінь алгебраїчного багаточлена з
дійсними коефіцієнтами, то
- корінь алгебраїчного багаточлена з
дійсними коефіцієнтами, то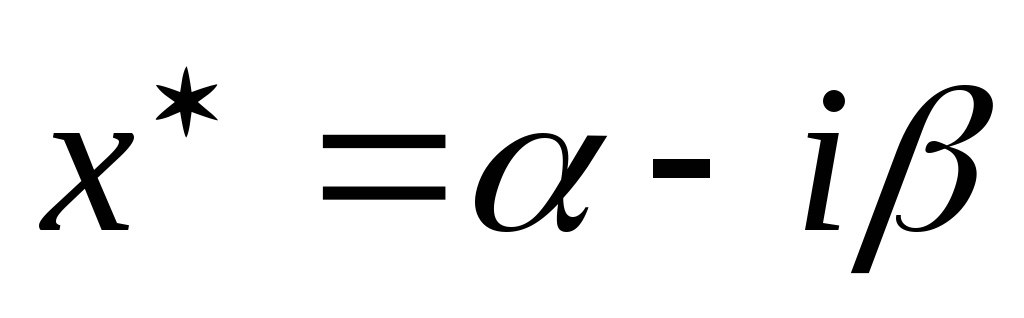 також є коренем тієї ж кратності.
також є коренем тієї ж кратності.
Наслідок. Алгебраїчний багаточлен з дійсними коефіцієнтами непарного степеня має хоча б один дійсний корінь.
Нехай
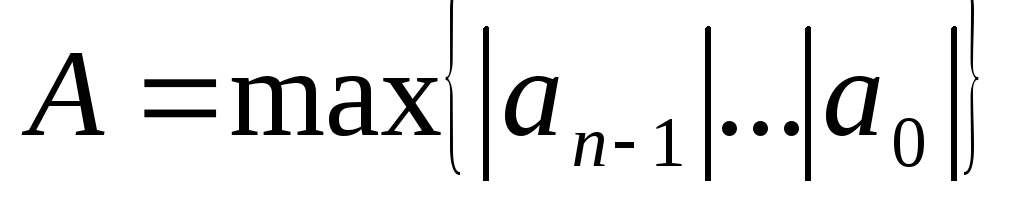 і
і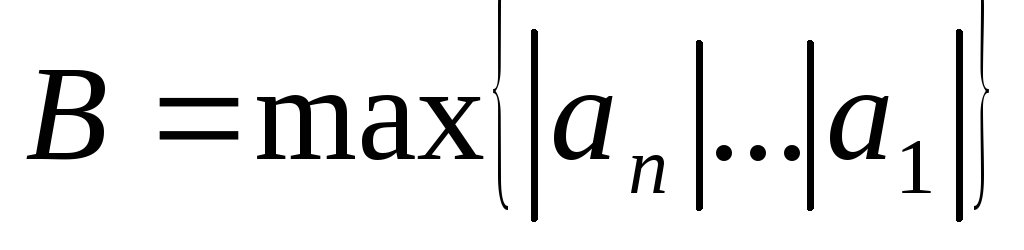 ,
де
,
де -
коефіцієнти (2),
-
коефіцієнти (2),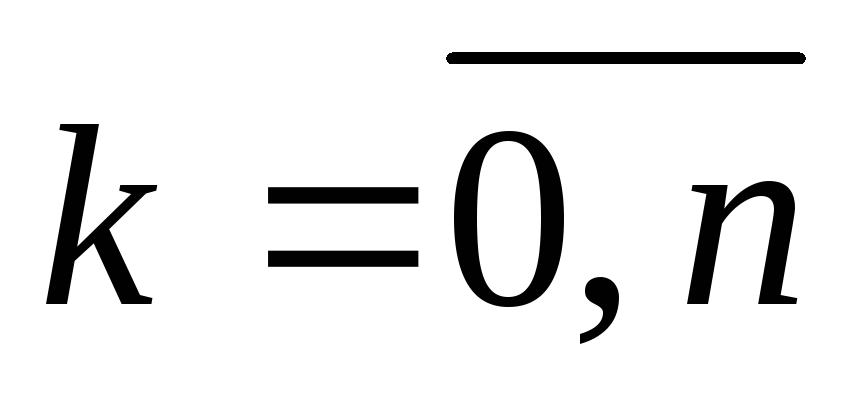 .
Тоді модулі всіх коренів рівняння (2)
задовольняють нерівності:
.
Тоді модулі всіх коренів рівняння (2)
задовольняють нерівності:
 .
.
На
практиці застосовують такі методи
відокремлення коренів:
засобами комп’ютерної графіки,
дослідження функцій і побудова графіка
функції, застосування методу половинного
поділу. Процес відокремлення коренів
починається з установлення знаків
![]() в граничних точках
в граничних точках![]() і
і![]() області її існування. Потім за допомогою
процесу половинного поділу визначають
знаки функції
області її існування. Потім за допомогою
процесу половинного поділу визначають
знаки функції![]() в точках поділу.
в точках поділу.
За
допомогою методу
підбирання можна,
застосовуючи комп'ютер, протабулювати
функцію
![]() з певним кроком і визначити проміжки,
на яких вона змінює знак.
з певним кроком і визначити проміжки,
на яких вона змінює знак.
Приклад
1. Відокремити
корені рівняння
![]() .
.
Розв’язування.
Тут
![]() .
Відповідно теоремі 2 рівняння має не
більше трьох дійсних коренів. Методом
підбирання визначимо, що
.
Відповідно теоремі 2 рівняння має не
більше трьох дійсних коренів. Методом
підбирання визначимо, що
|
|
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
+ |
|
|
- |
- |
+ |
+ |
+ |
- |
- |
+ |
+ |
Отже, рівняння має три корені. Інтервали коренів: (-3;-2); (0;1); (2;3) .
Використовують
також графічний
спосіб відокремлювання
коренів: будують графік функції
![]() і
наближено визначають області, де графік
перетинає вісь абсцис. Інколи зручно
рівняння (2.1) записати у вигляді
і
наближено визначають області, де графік
перетинає вісь абсцис. Інколи зручно
рівняння (2.1) записати у вигляді
![]() .
Значеннями коренів у цьому випадку
будуть абсциси точок перетину графіків
функцій
.
Значеннями коренів у цьому випадку
будуть абсциси точок перетину графіків
функцій![]() і
і![]() .
.
Приклад
2. Відокремити
корені рівняння
![]()
Розв’язування.
Перетворимо
його до вигляду
![]() і побудуємо графіки функцій
і побудуємо графіки функцій![]() і
і![]() .
З рис. 2.1 випливає, що рівняння має два
корені, і вони належать, відповідно,
проміжкам:
.
З рис. 2.1 випливає, що рівняння має два
корені, і вони належать, відповідно,
проміжкам:
![]() .
.
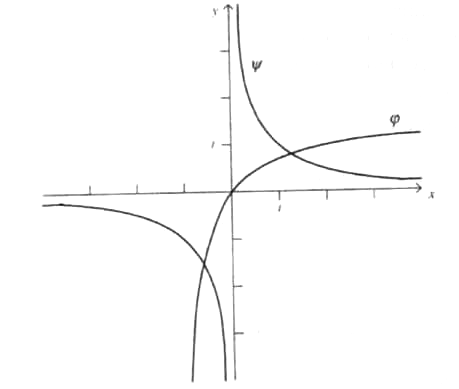
Рис. 1. Графічне відокремлення коренів.
Приклад
3. Відокремити
корені рівняння
![]() .
.
Розв'язування.
Тут
![]() ,
тому
,
тому![]() при
при![]() .
Звідси
.
Звідси![]()
![]() ;
;![]() .
Отже, рівняння має тільки два дійсні
корені, один з яких є в інтервалі
.
Отже, рівняння має тільки два дійсні
корені, один з яких є в інтервалі![]() ,
а інший ― в інтервалі
,
а інший ― в інтервалі![]() .
Уточнюємо інтервали знаходження коренів:
(-1;0) і (1;2).
.
Уточнюємо інтервали знаходження коренів:
(-1;0) і (1;2).
Приклад
4.
Відокремити корені рівняння
![]() .
Тут,
.
Тут,![]() .
На основі теореми 4 корені знаходяться
в інтервалі
.
На основі теореми 4 корені знаходяться
в інтервалі![]() <
<![]() <
2. Уточнюємо інтервал коренів:
<
2. Уточнюємо інтервал коренів:
|
|
-2 |
-1 |
|
|
1 |
2 |
|
|
- |
+ |
+ |
+ |
+ |
+ |
Для грубої оцінки похибки використовується теорема:
Теорема
5.
Нехай
![]() - точний, а
- точний, а![]() -
приблизний корені рівняння
-
приблизний корені рівняння![]() ,
які знаходяться на одному й тому ж
відрізку
,
які знаходяться на одному й тому ж
відрізку![]() ,
причому
,
причому![]() >0.
Тоді виконується оцінка:
>0.
Тоді виконується оцінка:![]() ,
де в якості
,
де в якості![]() можна брати
можна брати![]() .
.
Приклад
5.
Оцінити абсолютну похибку, якщо
![]() ,
а
,
а![]() .
.
![]() >0;
>0;
![]()
![]() <
<![]()
Взагалі універсальних методів відокремлення коренів не існує.
