
- •Методичні вказівки до практичних занять
- •Обчислювальна математика
- •2010 Зміст
- •Урахування похибок
- •1.1 Основні джерела похибок
- •1.2 Основні поняття
- •1.3 Правила обчислення похибок
- •1.4 Деякі правила обчислення максимальних граничних похибок
- •1.5 Приклади
- •1.6 Задачі
- •Методи розв'язування нелінійних рівнянь
- •2.1 Відокремлення коренів
- •2.2 Метод половинного поділу (бісекцій або діхотомії)
- •2.3 Метод січних (хорд, пропорційних частин)
- •2.4 Метод Ньютона (дотичних, лінеаризації)
- •2.4.1 Модифікований метод Ньютона
- •2.4.2 Метод Ньютона-Бройдена
- •2.5 Метод хорд та дотичних (комбінований метод)
- •2.6 Метод простих ітерацій
- •Методи розв'язування систем нелінійних рівнянь
- •3.1 Метод простих ітерацій
- •3.2 Метод Зейделя
- •3.3 Метод Ньютона
- •3.4 Модифікований метод Ньютона
- •Розв’язування систем лінійних алгебраїчних рівнянь (слар)
- •4.1 Метод ітерації
- •4.2 Зведення слар до вигляду, який придатний до застосування методу ітерації.
- •4.3 Метод Зейделя
- •4.4 Метод релаксації
- •4.5 Метод прогонки
- •4.6 Методика розв’язування задачі
- •5. Наближення функцій
- •5.1 Інтерполяція
- •5.2 Інтерполяційна формула Лагранжа
- •5.3 Оцінка похибки інтерполяційної формули Лагранжа
- •5.4 Збіжність функціонального інтерполяційного процесу неперервних функцій
- •5.5 Методика розв’язування задачі лінійної інтерполяції
- •5.6 Методика розв’язування задачі параболічної інтерполяції
- •5.7 Поліноми Чебишева
- •5.8 Інші методи інтерполяції. Інтерполяційний многочлен Ньютона
- •5.9 Методи інтегрально-диференціальної інтерполяції
- •5.10 Методи інтегрального згладжування
- •5.11 Метод найменших квадратів
- •5.12 Особливості мнк
- •5.13 Метод найкращого інтегрального наближення
- •5.14 Методи інтерполяції та згладжування на основі сплайнів
- •5.15 Інтерполяційні диференціальні кубічні сплайни
- •Список використаних джерел
2.4 Метод Ньютона (дотичних, лінеаризації)
Є
одним із найбільш популярних чисельних
методів. Має другий порядок збіжності
і допускає різні модифікації, які
застосовуються при розв’язуванні
нелінійних задач, систем нелінійних
рівнянь і сіткових рівнянь. Але він
застосовується при досить жорстких
обмеженнях [1] на функцію
![]()
Розглянемо
рівняння (2.1) і припустимо, що на відрізку
![]() функція
функція![]() двічі
диференційована, причому
двічі
диференційована, причому
![]() ´
´![]() і
і![]() ´´
´´![]() не
дорівнюють нулю на
не
дорівнюють нулю на
![]() .
Виберемо початкове наближення
.
Виберемо початкове наближення![]() і проведемо в точці
і проведемо в точці![]() дотичну до кривої
дотичну до кривої![]() (рис.
2.3). Рівняння дотичної має вигляд
(рис.
2.3). Рівняння дотичної має вигляд
![]() ´
´![]()
Нехай
![]() .
Знайдемо точку перетину
.
Знайдемо точку перетину![]() дотичної з віссюОХ
,
абсциса якої буде наближенням кореня
дотичної з віссюОХ
,
абсциса якої буде наближенням кореня
![]() :
:


Рис. 2.3. Геометрична інтерпретація методу Ньютона
У
точці
![]() знову проводимо дотичну до кривої та
отримаємо наступне наближення кореня.
Продовжуючи цей процес, отримаємо
ітераційну формулуметоду
Ньютона:
знову проводимо дотичну до кривої та
отримаємо наступне наближення кореня.
Продовжуючи цей процес, отримаємо
ітераційну формулуметоду
Ньютона:
![]() (2.5)
(2.5)
Геометрична
інтерпретація методу полягає в заміні
невеликої дуги кривої
![]() дотичною, яка проводиться в точці
дотичною, яка проводиться в точці![]() кривої (рис. 2.3).
кривої (рис. 2.3).
Метод Ньютона можна розглядати як частковий випадок методу простих ітерацій, якщо

Тоді
умова збіжності
![]() матиме вигляд
матиме вигляд

Загалом
метод Ньютона характеризується другим
порядком збіжності в околі кореня і
першим порядком – за його межами.
Суттєвим є вибір початкового наближення.
Невдало вибране початкове наближення,
наприклад,
![]() на
рис. 2.3, унеможливлює пошук кореня.
Початкове наближення
на
рис. 2.3, унеможливлює пошук кореня.
Початкове наближення
![]() треба
вибирати так, щоб виконувалася умова
треба
вибирати так, щоб виконувалася умова
![]() >0 (2.6)
>0 (2.6)
Теорема 6. Достатні умови збіжності методу Ньютона.
Нехай виконуються такі умови:
функція
 визначена та двічі диференційована на
відрізку
визначена та двічі диференційована на
відрізку ;
;відрізку
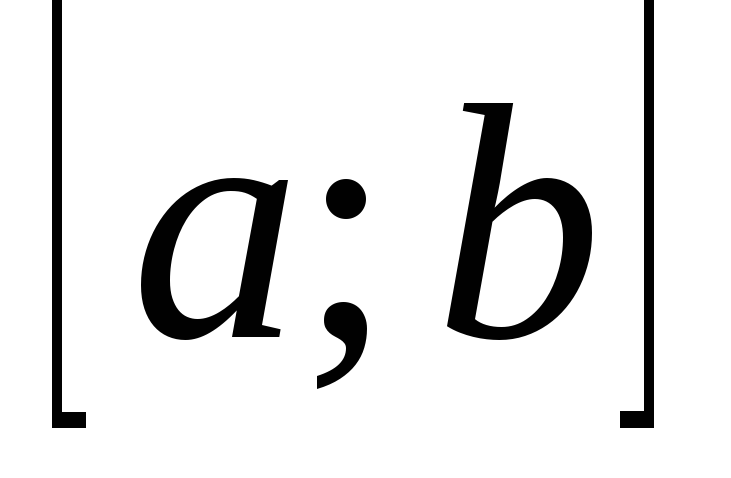 належить тільки один простий корінь
належить тільки один простий корінь так, що
так, що <0;
<0;похідні
 та
та на
на зберігають знак, і
зберігають знак, і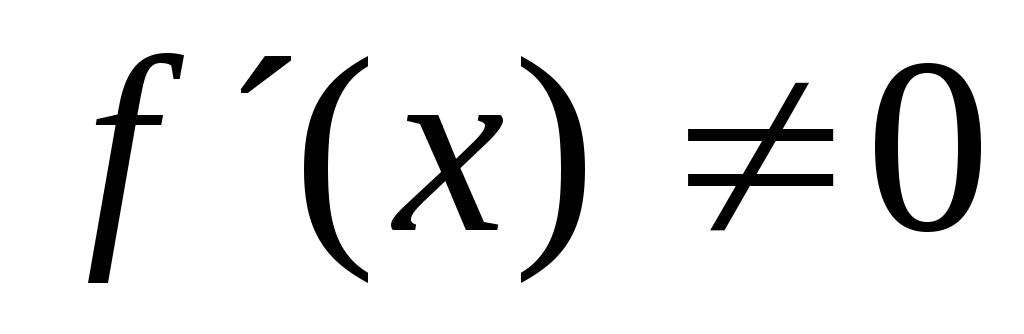 ;
;початкове наближення
 задовольняє нерівності
задовольняє нерівності >0
(знаки функцій
>0
(знаки функцій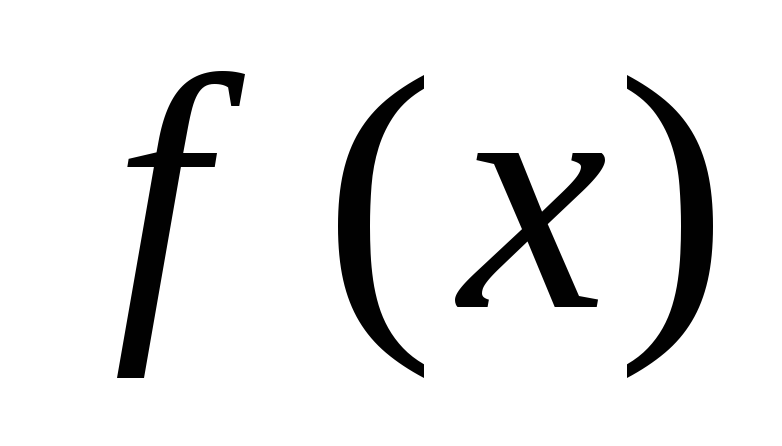 та
та в точці
в точці збігаються).
збігаються).
Тоді
методом Ньютона (2.5) можна визначити
корінь рівняння
![]() з довільною точністю.
з довільною точністю.
Теорема 7. Достатні умови збіжності методу Ньютона.
Нехай:
-
![]() визначена у відкритому інтервалі
визначена у відкритому інтервалі![]() ;
;
-
![]() є ліпшиць-неперервною з константою
є ліпшиць-неперервною з константою![]() для
для![]() ;
;
-
для деякого
![]() >0
виконується умова
>0
виконується умова![]() для
для![]() .
.
Тоді,
якщо рівняння
![]() має розв’язок
має розв’язок![]() ,
то послідовність
,
то послідовність![]() ,
яка визначається (2.5) існує та збігається
до
,
яка визначається (2.5) існує та збігається
до![]() .
Більш того
.
Більш того![]()
Точність
![]() -го
наближення
-го
наближення![]() :
:![]() ,
де
,
де![]() -
найменше значення
-
найменше значення![]() на відрізку
на відрізку![]() .
Інша оцінка:
.
Інша оцінка:![]() ,
де
,
де![]() .
.
Зауваження
1.
Якщо
![]() ,
то
,
то![]() -
кратний корінь, а метод Ньютона збігається
лінійно.
-
кратний корінь, а метод Ньютона збігається
лінійно.
Зауваження
2.
Метод Ньютона може застосовуватися не
тільки для знаходження простих коренів,
тобто коли на відрізку
![]() ,
який містить корінь, не виконується
умова
,
який містить корінь, не виконується
умова![]() <0.
<0.
Зауваження
3.
Виконання умов теорем 6,7 гарантує
збіжність метода Ньютона тільки для
"гарного" початкового наближення
![]() :
:![]() >0
і
>0
і![]() в околі кореня
в околі кореня![]() .
.
Приклад
1.
Обчислити методом Ньютона від’ємний
корінь рівняння
![]() з 5 вірними знаками.
з 5 вірними знаками.
Інтервал
кореня:
![]() ,
причому
,
причому![]() ´
´![]() <
<![]() >0
при
>0
при![]() ,
,![]()
Так
як
![]() >0
і
>0
і![]() ,
то за вихідне наближення приймаємо
,
то за вихідне наближення приймаємо![]() .
Послідовні наближення наведені в таблиці
.
Послідовні наближення наведені в таблиці![]() ;
;![]()
![]()
![]()
![]() і т. д.
і т. д.
Таблиця 2.1
Результати обчислень
|
|
|
|
|
|
|
0 |
-11 |
3453 |
-5183 |
0,66622 |
|
1 |
-10,33378 |
308,0708 |
-4277,077 |
0,07203 |
|
2 |
-10,26175 |
3,28807 |
-4185,823 |
0,00079 |
|
3 |
-10,26098 |
0,06536 |
-4184,8545 |
0,00002 |
|
4 |
-10,26096 |
|
|
|
Відповідь:
![]()
Приклад
2.
Знайти за методом Ньютона найменший
додатний корінь рівняння
![]() з точністю до 0,0001.
з точністю до 0,0001.
Будуємо
графіки
![]() і
і![]() .
Інтервал кореня
.
Інтервал кореня![]() .
.
Запишемо
рівняння у вигляді
![]() .
Тоді:
.
Тоді:![]() .
.
Так
як
![]() <0,
<0,![]() <0
при
<0
при![]() і
і![]() <0,
то за початкове наближення приймаємо
<0,
то за початкове наближення приймаємо![]() .
.
Таблиця 2.1
Результати обчислень
|
|
|
|
|
|
|
0 |
|
-1 |
-4,712 |
-0,21222 |
|
1 |
4,50017 |
-0,02974 |
-4,3993 |
-0,00676 |
|
2 |
4,49341 |
-0,00012 |
-4,38604 |
-0,00002 |
Для
оцінки похибки знаходимо:
![]() ,
тому що
,
тому що![]() <0
при
<0
при![]() .
Тоді
.
Тоді![]() <0,00003,
тобто:
<0,00003,
тобто:![]() .
Враховуючи попередній аналіз, остаточно:
.
Враховуючи попередній аналіз, остаточно:![]() ,
де
,
де![]() .
.
Приклад
3.
Методом Ньютона з точністю
![]() знайти корінь трансцендентного рівняння
знайти корінь трансцендентного рівняння![]() ,
причому шуканий корінь
,
причому шуканий корінь![]() .
.
На
множині
![]() виконуються умови теореми 1, які
забезпечують збіжність метода дотичних
виконуються умови теореми 1, які
забезпечують збіжність метода дотичних![]() >0
на множині
>0
на множині![]() .
.![]() <0
<0![]() >0.
Тоді
>0.
Тоді![]() >0.
Тому початкове наближення
>0.
Тому початкове наближення![]() .
.
Таблиця 2.2
Результати обчислень
|
|
0 |
1 |
2 |
3 |
|
|
1,000 |
0,73304 |
0,70381 |
0,703467 |
|
|
– |
0,27 |
0,029 |
0,00034 |
|
|
0,63212 |
0,05690 |
0,00065 |
|
Відповідь:![]() .
.
Приклад
4.
Побудувати
ітераційну формулу Ньютона для рівняння
![]() .
.
Розв’язування.
Застосовуючи
(2.5). отримаємо

Це відома формула Герона для наближеного відшукання квадратного кореня числа а .
Приклад
5.
Знайти корінь рівняння
![]() методом хорд з точністю
методом хорд з точністю![]() .
.
Відокремимо
корінь на відрізку
![]() .
Тоді для
.
Тоді для![]() :
:
![]()
Порівняємо метод Ньютона з методом хорд (приклад 2 розділ 2.3). За 5 кроків метод Ньютона дає похибку обчислень майже у 10000 раз меншу.
Приклад 6. Порівняємо метод Ньютона з методом хорд. У таблиці наведено хід ітерацій у разі добування квадратного кореня з а = 16 . Перші два наближення взяті однаковими. З порівняння видно, що метод хорд збігається повільніше.
![]()
![]()
![]()
![]() ;
;
![]() .
.
Таблиця 2.3
Результати обчислень
|
n |
|
хп за методом хорд |
|
0 |
2,0000 |
2,0000 |
|
1 |
5,0000 |
5,0000 |
|
2 |
4,1000 |
3,7143 |
|
3 |
4,0012 |
3,9673 |
