
- •А.А. Силич, т.А. Миронова, ф.В. Авдощенко
- •Введение
- •Глава 1. Метод проецирования
- •1.1. Центральная проекция
- •1.2. Параллельная проекция
- •1.2.1. Свойства параллельных проекций
- •1.3. Показатели искажения
- •1.4. Аксонометрические проекции
- •Изображения точки
- •Рис 1.11. Аксонометрическое изображение модели
- •1.4.1.Направление аксонометрических осей и показатели
- •1.4.2. Построение окружности в аксонометрических проекциях
- •Глава 2. Точка, прямая, плоскость
- •2.1. Ортогональные проекции точки
- •2.1.1. Безосный эпюр
- •Б) на две плоскости проекции; в) безосный
- •2.2. Ортогональные проекции прямой
- •2.2.1. Прямые частного положения
- •Рис 2.4 Прямые частного положения
- •Рис 2.5 Проекция прямой частного положения
- •2.3. Взаимное положение прямых линий
- •А) параллельные; б) пересекающиеся; в) скрещивающиеся
- •2.3.1. Конкурирующие точки
- •2.4. Проекции плоских углов
- •2.4.1. Теорема о проекциях прямого угла
- •А) на фронтальной плоскости проекции; б) на горизонтальной плоскости проекции
- •Рис 2.12 Проекция прямого угла
- •2.5. Ортогональные проекции плоскости
- •А) в диметрии; б) на эпюре
- •2.5.1. Прямая и точка в плоскости
- •А) заданной прямоугольником; б) заданной следом
- •А) в диметрии; б) на эпюре
- •3.3. Пересечение плоскости с прямой общего положения
- •3.4 Взаимное пересечение плоскостей общего положения
- •Рис 3.6. Построение линии пересечения двух плоскостей, не имеющих общих точек
- •3.5. Прямая, параллельная плоскости
- •3.6. Параллельные плоскости
- •3.7. Прямая, перпендикулярная плоскости
- •3.8. Взаимно перпендикулярные плоскости
- •Рис 3.12 Взаимно перпендикулярные плоскости
- •Глава 4. Способы преобразования чертежа
- •4.1. Способ замены плоскостей проекций
- •Преобразование чертежа точки и прямой
- •Рис 4.2. Преобразование чертежа точки на эпюре
- •Рис 4.3. Преобразование чертежа прямой
- •Рис 4.4. Определение натуральной длины отрезка а) и угла α; б) и угла β
- •Рис 4.5. Преобразование чертежа
- •Рис 4.7. Преобразование плоскости общего положения
- •Рис 4.8. Преобразование горизонтально проецирующей плоскости в плоскость уровня
- •Рис 4.9. Преобразование плоскости общего положения в плоскость уровня
- •Рис 4.10. Вращение точки вокруг оси в диметрии
- •Рис 4.11. Вращение точки вокруг оси на юпюре
- •4.2.2. Вращение без указания осей на чертеже –
- •Способом плоскопараллельного перемещения
- •4.2.3. Способ вращения вокруг линии уровня
- •A) б)
- •Глава 5. Многогранники
- •5.1. Общие положения
- •Г) призма усеченная
- •Грани вcc’в’
- •Грани авв’а’
- •Грани sвс
- •5.2. Пересечение многогранников плоскостью
- •Положения и определение натуральной величины сечения
- •5.3. Пересечение многогранников с прямой линией
- •С пирамидой
- •5.4. Взаимное пересечение многогранников
- •5.5. Развертки многогранников
- •Усеченной призмы
- •Глава 6. Кривые линии
- •6.1. Основные определения и проекции кривых
- •6.2. Пространственные кривые
- •Глава 7. Кривые поверхности
- •7.1. Общие сведения
- •7.2. Поверхности вращения
- •7.3. Пересечение поверхности вращения плоскостью
- •7.3.1. Цилиндр. Возможные сечения
- •7.3.2. Конус. Возможные сечения
- •7.3.3. Пересечение поверхности вращения с плоскостью
- •Положения заданной прямыми линиями ав и вс
- •7.4. Пересечение поверхности вращения с прямой линией
- •7.5. Взаимное пересечение поверхностей
- •7.5.1. Способ вспомогательных секущих плоскостей
- •7.5.2. Способ вспомогательных сферических поверхностей
- •7.6. Развертка поверхности вращения
- •7.7. Развертываемые и косые поверхности
- •7.7.1. Линейчатые развертываемые поверхности.
- •Заключение
- •Список литературы
- •Содержание
- •Глава 3. Относительное положение прямой и
7.7. Развертываемые и косые поверхности
7.7.1. Линейчатые развертываемые поверхности.
Линейчатые развертываемые поверхности (торсы) образуются закономерным движением в пространстве прямой – образующей по направляющим линиям.
У торсов две бесконечно близких образующих или пересекаются или параллельны, поэтому поверхности относят к развертываемым.
Если образующая прямая непрерывно перемещается по какой-то пространственной кривой, оставаясь при этом касательной к ней во всех своих положениях, то образуется торс, называемый поверхностью с ребром возврата (рис.7.21).
Кривая К (ребро возврата) является множеством точек возврата кривых, получающихся в плоскостях, нормальных к образующим в точках их касания с направляющей. Поверхность имеет две полы.
Определитель поверхности записывается ФКА, где К – ребро возврата, т.е. поверхность определяется положением ребра возврата, А - алгоритм движения образующей (касание). Если ребро возврата вырождается в точку, то поверхность с ребром возврата преобразуется в коническую или цилиндрическую поверхности.
Таким образом, к торсам относятся три вида поверхностей: поверхность с ребром возврата, коническая и цилиндрическая. Последние широко распространены в технике и требуют более подробного рассмотрения.
Цилиндрическая поверхность получается при движении прямой, перемещающейся по кривой направляющей, параллельно заданному направлению. Определитель поверхности: Фn, lА, где n – направляющая, l – образующая, А – алгоритм образования поверхности, (l //b), b – направление образующей (рис.7.22).
Если направляющая поверхности произвольная кривая, то образуется цилиндрическая поверхность общего вида.
Цилиндрическая поверхность безгранична и может пересекать плоскость проекций, оставляя на ней след m (см. рис.7.22). След является одной из направляющих поверхности и может служить для задания ее на чертеже. m (mH, mV ) – горизонтальный след поверхности. Часть цилиндрической поверхности, заключенная между двумя параллельными плоскостями пересекающими все образующие, называется цилиндром. Сечение цилиндра плоскостью, перпендикулярной образующим, называют нормальным. Видом нормального сечения определяется название цилиндра.

Рис. 7.21. Поверхность с ребром возврата
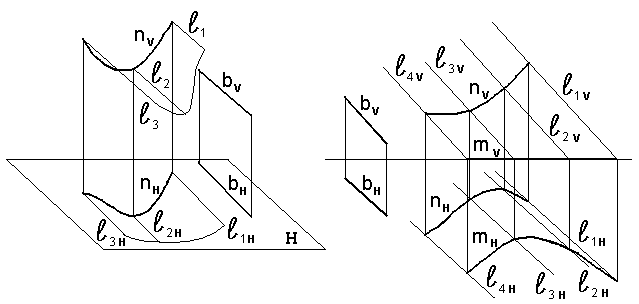
Рис. 7.22. Цилиндрическая поверхность общего вида
Если в нормальном сечении круг, то цилиндр круговой, эллипс – эллиптический, парабола – параболический и т.д.
Если за основание цилиндра принято нормальное сечение, то он прямой, если любое другое – наклонный. Прямой круговой цилиндр идентичен цилиндру вращения. Только в круговой цилиндр может быть вписан шар. Основанием наклонного кругового цилиндра является эллипс, малая ось которого равна диаметру окружности нормального сечения, а большая ось зависит от направления образующей.
На рис.7.23 показан прямой эллиптический цилиндр. Круговое сечение эллиптического цилиндра может быть получено при пересечении цилиндра со сферой, диаметр которой равен большой оси эллипса основания и, которая имеет с цилиндром двойное прикосновение (см. рис.7.23).
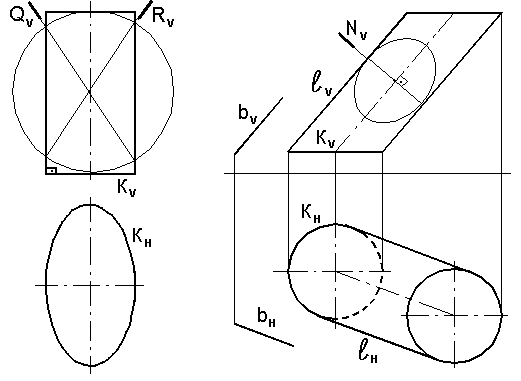
Рис. 7.23. Прямой Рис. 7.24. Наклонный эллиптический
эллиптический цилиндр цилиндр
У наклонного эллиптического цилиндра с круговым основанием диаметр последнего равен большой оси нормального сечения (рис.7.24), а малая ось определяется направлением образующей.
Коническая поверхность получается при движении прямой образующей, пересекающей кривую направляющую и проходящую во всех своих положениях через неподвижную точку, называемую вершиной поверхности. Определитель конической поверхности Фn, SА, где n – направляющая кривая, S – вершина поверхности, l – образующая поверхности (рис.7.25).
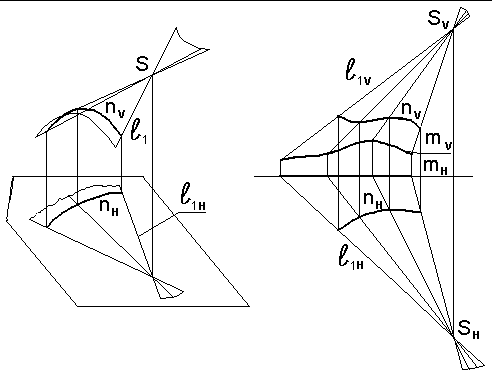
Рис. 7.25. Коническая поверхность общего вида
Коническая поверхность простирается неограниченно по обе стороны вершины и является двуполостной. Она называется поверхностью общего вида, если направляющая ее – произвольная кривая. Пересекаясь с плоскостями проекций, коническая поверхность оставляет на них следы (см. рис.7.25), mV – фронтальный след поверхности. Коническая поверхность может быть задана следом и вершиной.
Осью конической поверхности называют линию пересечения хотя бы двух ее плоскостей симметрии (линия SM на рис.7.26).
Часть конической поверхности, заключенная между вершиной и плоскостью, пересекающей все образующие, называется конусом.
Сечение конуса, перпендикулярное его оси, называется нормальным. Видом нормального сечения определяется название конуса.
Если нормальное сечение принято за основание конуса – конус прямой, если любое другое сечение – конус наклонный.
Только круговой конус является множеством прямых касательных к сфере, исходящих из одной точки (вершины), поэтому только в круговой конус можно вписать шар.
На рис.7.27 показан наклонный круговой конус, а на рис.7.26 – наклонный эллиптический конус с круговым основанием.
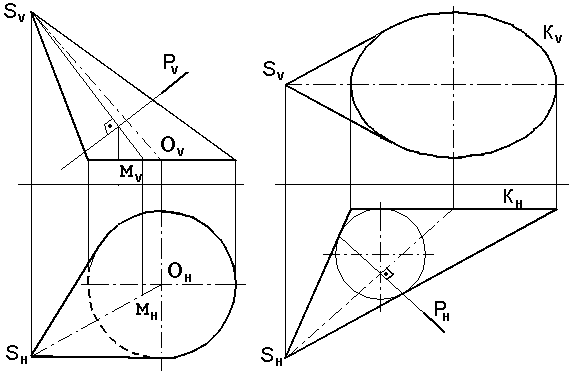
Рис. 7.26. Наклонный Рис. 7.27. Наклонный круговой
эллиптический конусконус
с круговым основанием
Круговое сечение эллиптического конуса может быть получено как линия пересечения его со сферой, имеющей с конусом двойное прикосновение (подобно тому, как оно было получено для эллиптического цилиндра). Осью конуса является биссектриса угла при вершине конуса.
