
- •А.А. Силич, т.А. Миронова, ф.В. Авдощенко
- •Введение
- •Глава 1. Метод проецирования
- •1.1. Центральная проекция
- •1.2. Параллельная проекция
- •1.2.1. Свойства параллельных проекций
- •1.3. Показатели искажения
- •1.4. Аксонометрические проекции
- •Изображения точки
- •Рис 1.11. Аксонометрическое изображение модели
- •1.4.1.Направление аксонометрических осей и показатели
- •1.4.2. Построение окружности в аксонометрических проекциях
- •Глава 2. Точка, прямая, плоскость
- •2.1. Ортогональные проекции точки
- •2.1.1. Безосный эпюр
- •Б) на две плоскости проекции; в) безосный
- •2.2. Ортогональные проекции прямой
- •2.2.1. Прямые частного положения
- •Рис 2.4 Прямые частного положения
- •Рис 2.5 Проекция прямой частного положения
- •2.3. Взаимное положение прямых линий
- •А) параллельные; б) пересекающиеся; в) скрещивающиеся
- •2.3.1. Конкурирующие точки
- •2.4. Проекции плоских углов
- •2.4.1. Теорема о проекциях прямого угла
- •А) на фронтальной плоскости проекции; б) на горизонтальной плоскости проекции
- •Рис 2.12 Проекция прямого угла
- •2.5. Ортогональные проекции плоскости
- •А) в диметрии; б) на эпюре
- •2.5.1. Прямая и точка в плоскости
- •А) заданной прямоугольником; б) заданной следом
- •А) в диметрии; б) на эпюре
- •3.3. Пересечение плоскости с прямой общего положения
- •3.4 Взаимное пересечение плоскостей общего положения
- •Рис 3.6. Построение линии пересечения двух плоскостей, не имеющих общих точек
- •3.5. Прямая, параллельная плоскости
- •3.6. Параллельные плоскости
- •3.7. Прямая, перпендикулярная плоскости
- •3.8. Взаимно перпендикулярные плоскости
- •Рис 3.12 Взаимно перпендикулярные плоскости
- •Глава 4. Способы преобразования чертежа
- •4.1. Способ замены плоскостей проекций
- •Преобразование чертежа точки и прямой
- •Рис 4.2. Преобразование чертежа точки на эпюре
- •Рис 4.3. Преобразование чертежа прямой
- •Рис 4.4. Определение натуральной длины отрезка а) и угла α; б) и угла β
- •Рис 4.5. Преобразование чертежа
- •Рис 4.7. Преобразование плоскости общего положения
- •Рис 4.8. Преобразование горизонтально проецирующей плоскости в плоскость уровня
- •Рис 4.9. Преобразование плоскости общего положения в плоскость уровня
- •Рис 4.10. Вращение точки вокруг оси в диметрии
- •Рис 4.11. Вращение точки вокруг оси на юпюре
- •4.2.2. Вращение без указания осей на чертеже –
- •Способом плоскопараллельного перемещения
- •4.2.3. Способ вращения вокруг линии уровня
- •A) б)
- •Глава 5. Многогранники
- •5.1. Общие положения
- •Г) призма усеченная
- •Грани вcc’в’
- •Грани авв’а’
- •Грани sвс
- •5.2. Пересечение многогранников плоскостью
- •Положения и определение натуральной величины сечения
- •5.3. Пересечение многогранников с прямой линией
- •С пирамидой
- •5.4. Взаимное пересечение многогранников
- •5.5. Развертки многогранников
- •Усеченной призмы
- •Глава 6. Кривые линии
- •6.1. Основные определения и проекции кривых
- •6.2. Пространственные кривые
- •Глава 7. Кривые поверхности
- •7.1. Общие сведения
- •7.2. Поверхности вращения
- •7.3. Пересечение поверхности вращения плоскостью
- •7.3.1. Цилиндр. Возможные сечения
- •7.3.2. Конус. Возможные сечения
- •7.3.3. Пересечение поверхности вращения с плоскостью
- •Положения заданной прямыми линиями ав и вс
- •7.4. Пересечение поверхности вращения с прямой линией
- •7.5. Взаимное пересечение поверхностей
- •7.5.1. Способ вспомогательных секущих плоскостей
- •7.5.2. Способ вспомогательных сферических поверхностей
- •7.6. Развертка поверхности вращения
- •7.7. Развертываемые и косые поверхности
- •7.7.1. Линейчатые развертываемые поверхности.
- •Заключение
- •Список литературы
- •Содержание
- •Глава 3. Относительное положение прямой и
Рис 4.9. Преобразование плоскости общего положения в плоскость уровня
Вращение вокруг оси, перпендикулярной к плоскости
проекций
Допустим, что точка А, расположенная в пространстве вращается вокруг оси i, перпендикулярной к фронтальной плоскости проекций V (рис.4.10а).
Проекцией вращающейся точки А на фронтальной плоскости проекций является окружность, а на горизонтальной прямая линия перпендикулярная оси вращения или параллельно оси Х (рис.4.11). Если ось вращения i перпендикулярна к плоскости Н, то горизонтальная проекция точки описывает окружность, а ее фронтальная проекция перемещается параллельно оси Х (рис.4.11).
Задача: Повернуть отрезок АВ до положения прямой уровня (рис.4.12).
Решение. Повернем отрезок, например, до положения фронтали. Для этого за ось вращения примем горизонтально-проецирующую прямую i, проходящую через точку В. При вращении точка В остается неподвижной, остается повернуть вокруг оси i точку А до положения, чтобы заданный отрезок стал параллельным фронтальной плоскости

Рис 4.10. Вращение точки вокруг оси в диметрии

Рис 4.11. Вращение точки вокруг оси на юпюре
проекций. Горизонтальная проекция траектории точки А есть дуга окружности, а фронтальная проекция есть прямая параллельная оси Х. Для поворота отрезка АВ до положения горизонтали нужно за ось вращения принять фронтально-проецирующую прямую, проведенную через какую-нибудь точку отрезка АВ.
При решении этих задач можно определить натуральную величину углов наклона отрезка к плоскостям проекций и . На рис. 4.10 показан, например, угол .
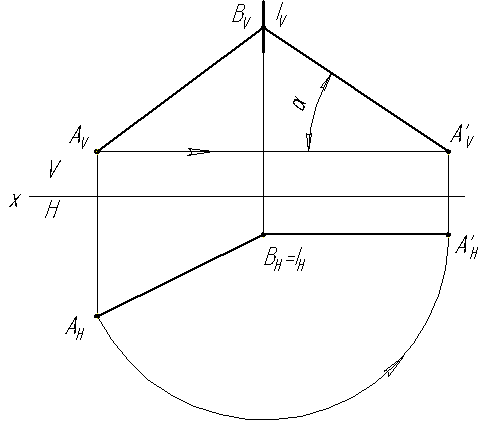
Рис.4.10 Вращение прямой вокруг проецирующей оси
4.2.2. Вращение без указания осей на чертеже –
плоскопараллельное перемещение
Способ вращения вокруг оси перпендикулярной плоскости проекций не всегда удобен, так как новое положение проекций формы может налагаться на заданное изображение. Проще и рациональней использовать способ плоскопараллельного перемещения. Он заключается в том, что используемые геометрические формы перемещаются в плоскостях, параллельных плоскостям проекций, причем взаимная связь элементов формы не изменяется.
Задача: Прямую общего положения преобразовать в горизонтально-проецирующую.
Решение. На рис.4.11 сначала отрезок АВ общего положения переместили в положение фронтали, для этого построили А1НВ1Н = АН ВН параллельно фронтальной плоскости на произвольном расстоянии от оси Х. Одновременно все точки отрезка на фронтальной проекции движутся в горизонтальных направлениях к соответствующим каждой точке линиям связи с новыми горизонтальными проекциями этих точек. Второе перемещение, цель которого преобразовать отрезок АВ в проецирующее вертикальное положение, выполнено параллельно фронтальной плоскости проекций.
При перемещении нескольких связанных между собой геометрических элементов для решения метрических задач необходимо оставлять неизменным их взаимное размещение, так как при нарушении этого положения ответ не будет искомым.
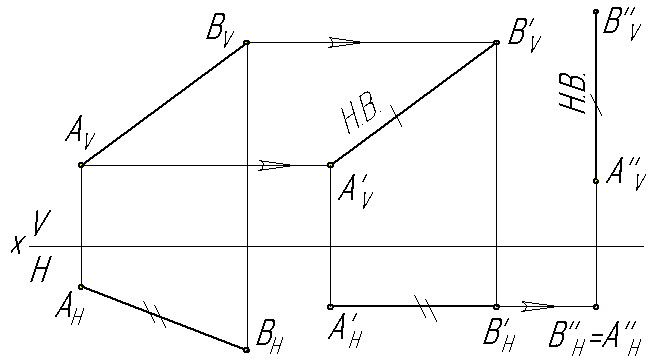
Рис.4.11 Плоскопараллельное перемещение отрезка АВ
Задача: Определить натуральную величину треугольника АВС (Рис.4.12).
Решение.
1. Провести горизонталь А1 в треугольнике АВС.
2. Горизонталь А’H1’H построить перпендикулярно фронтальной плоскости на произвольном расстоянии от нее.
3. Методом засечек относительно горизонтали А’Н1’Н перенести горизонтальную проекцию треугольника в положение А’НВ’НС’Н (АНВНСН = А’НВ’НС’Н). По горизонтальной проекции треугольника построить фронтальную. Таким образом треугольник общего положения преобразовали во фронтально-проецирующую плоскость. Этим нашли угол наклона плоскости к горизонтальной плоскости проекций.
4. Перенести новую фронтальную проекцию треугольника А’VВ’VC’V в положение А’’VВ’’VС’’V параллельное горизонтальной плоскости проекций, достроить горизонтальную проекцию А’’НВ’’НС’’Н. Этим преобразовали фронтально-проецирующую плоскость в плоскость уровня, а именно в горизонтальную, следовательно горизонтальная проекция А’’НВ’’НС’’Н в натуральной величине.
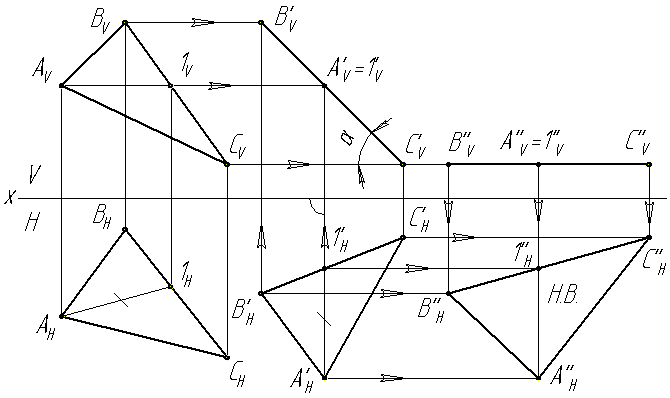
Рис.4.12 Определение натуральной величины треугольника
