15 Вопрос.
Алгебраические
Алгебраическая функция — функция, которая в окрестности каждой точки области определения может быть задана неявно с помощью алгебраического уравнения.
Более точное определение:
Функция 
называется
алгебраической в точке 
,
если существует окрестность точки 
,
в которой верно тождество
где 
есть многочлен от n +
1 переменной.
Функция называется алгебраической, если она является алгебраической в каждой точке области определения.
Например,
функция действительного переменного 
является
алгебраической на интервале (
− 1,1) в
поле действительных чисел, так как она
удовлетворяет уравнению
Существует аналитическое
продолжение функции 
на комплексную
плоскость, с вырезанным отрезком [
− 1,1] или
с двумя вырезанными лучами 
и 
.
В этой области полученная функция
комплексного переменного является
алгебраической и аналитической.
Известно, что если функция является алгебраической в точке, то она является и аналитической в данной точке. Обратное неверно. Функции, являющиеся аналитическими, но не являющиеся алгебраическими, называются трансцендентными.
Трансцендентные
Свойства
Множество трансцендентных чисел континуально.
Каждое
трансцендентное вещественное
число является иррациональным,
но обратное неверно. Например, число 
—
иррациональное, но не трансцендентное:
оно является корнем многочлена 
(и
потому является алгебраическим).
Примеры
Основание
натуральных логарифмов 
.
Число 
.
Десятичный
логарифм любого
целого числа, кроме чисел вида 
.
, 
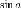и 
,
для любого ненулевого алгебраического
числа 
.
Элементарные функции
Элементарные функции— функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:
многочлен,
рациональная,
степенная,
показательная и логарифмическая,
тригонометрические и обратные тригонометрические.
Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения. Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.
Элементарные функции разделяются на алгебраические и трансцендентные.
Специальные функции
Специальные функции — встречающиеся в различных приложениях математики (чаще всего — в различных задачах математической физики) функции, которые не выражаются через элементарные функции. Специальные функции представляются в виде рядов или интегралов.
Специальные функции возникают обычно из следующих соображений:
«неберущиеся» интегралы;
решения трансцендентных уравнений, не выражающиеся в элементарных функциях;
решения дифференциальных уравнений, не выражающиеся в элементарных функциях;
ряды, не сходящиеся к элементарным функциям;
математическое выражение свойств чисел;
необходимость задания функции с необычными свойствами.
Эта разделение не является строгим, поскольку, например, большинство неэлементарных решений дифференциальных уравнений удалось выразить через неберущийся интеграл или в виде ряда. Поэтому не существует строгой классификации трансцендентных функций
Большинство специальных функций являются трансцендентными.
