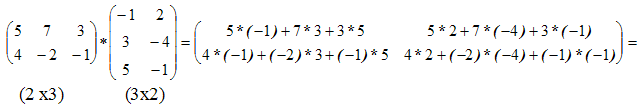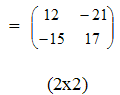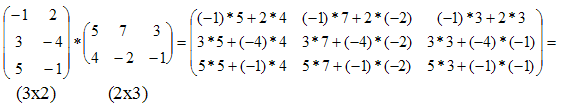5 Вопрос.

Определения.

Матрицей называется прямоугольная  таблица чисел  или буквенных выражений, содержащая m строк и n столбцов:

,

 называют  элементами  матрицы.

Матрица, у которой число строк равно числу столбцов, т.е. m=n, называется квадратной матрицей, а число n называется порядком матрицы:

A = 

 Элементы   образуют главную диагональ квадратной матрицы. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны нулю, то матрицу называют диагональной. Если в диагональной матрице все элементы главной диагонали равны между собой, то ее называют скалярной.

Если в скалярной матрице все элементы главной диагонали равны единице, то матрицу называют единичной и обозначают буквой E .

Если все элементы матрицы  равны  0, то матрица называется нулевой и ее обозначают буквой O.

Две матрицы считаются равными, если они одинакового размера, и элементы, стоящие на пересечении строк и столбцов с одинаковыми номерами, равны, т.е. если

Сложение матриц.

Суммой матриц одной и той же размерности называется матрица размерности , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B:

Матрицы разных размерностей складывать нельзя.

Пример1..

Свойства сложения матриц.1. Коммутативность.A+B=B+A2. Ассоциативность. (A+B)+C=A+(B+C)

Умножение матриц, транспонирование матриц.

Матрица C, элементы которой с_ij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α:

Пример 2. .

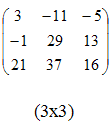
Произведением матрицы  размерности на матрицу размерности называется матрица размерности , где:

Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример 3.

Пример 4.

Результатом транспонирования матрицы размерности является матрица  размерности , где 

Пример 5.

Свойства транспонированных матриц.

1). Если E-единичная матрица, то E=E^T.

2). Двукратное транспонирование не изменяет матрицу (A^T)^T=A.

3). Транспонирование суммы матриц равносильно сложению транспонированных матриц: (A+B)^T=A^T+B^T

4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: .

5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице: (A^-1)^T=(A^T)^-1 .

6). Если транспонированная матрица A^T совпадает с данной матрицей A, то матрица A называется симметрической.

Определения.

Матрицей называется прямоугольная  таблица чисел  или буквенных выражений, содержащая m строк и n столбцов:

,

 называют  элементами  матрицы.

Матрица, у которой число строк равно числу столбцов, т.е. m=n, называется квадратной матрицей, а число n называется порядком матрицы:

A = 

 Элементы  образуют главную диагональ квадратной матрицы. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны нулю, то матрицу называют диагональной. Если в диагональной матрице все элементы главной диагонали равны между собой, то ее называют скалярной.

Если в скалярной матрице все элементы главной диагонали равны единице, то матрицу называют единичной и обозначают буквой E .

Если все элементы матрицы  равны  0, то матрица называется нулевой и ее обозначают буквой O.

Две матрицы считаются равными, если они одинакового размера, и элементы, стоящие на пересечении строк и столбцов с одинаковыми номерами, равны, т.е. если

Сложение матриц.

Суммой матриц одной и той же размерности называется матрица размерности , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B:

Матрицы разных размерностей складывать нельзя.

Пример1..

Свойства сложения матриц.1. Коммутативность.A+B=B+A2. Ассоциативность. (A+B)+C=A+(B+C)

Умножение матриц, транспонирование матриц.

Матрица C, элементы которой с_ij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α:

Пример 2. .

Произведением матрицы  размерности на матрицу размерности называется матрица размерности , где:

Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример 3.

Пример 4.

Результатом транспонирования матрицы размерности является матрица  размерности , где 

Пример 5.

Свойства транспонированных матриц.

1). Если E-единичная матрица, то E=E^T.

2). Двукратное транспонирование не изменяет матрицу (A^T)^T=A.

3). Транспонирование суммы матриц равносильно сложению транспонированных матриц: (A+B)^T=A^T+B^T

4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: .

5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице: (A^-1)^T=(A^T)^-1 .

6). Если транспонированная матрица A^T совпадает с данной матрицей A, то матрица A называется симметрической.
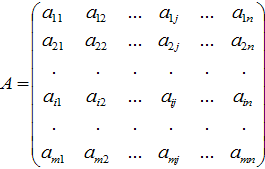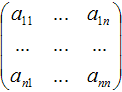
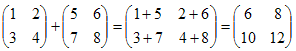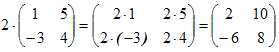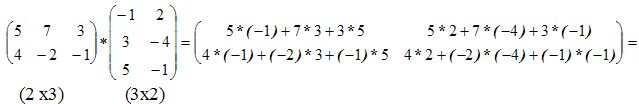
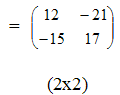
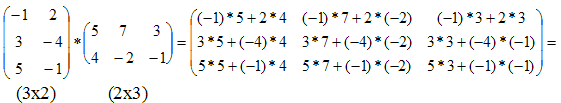
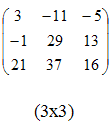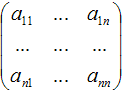
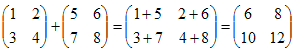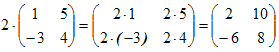