27 Вопрос.

Первообразнойилипримитивной функцией(иногда называют также антипроизводной) даннойфункцииf называют такую F,производнаякоторой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция является первообразной. Так как производнаяконстантыравнанулю,будет иметьбесконечноеколичество первообразных; таких какили… и т. д.; таким образомсемействопервообразных функции x2 можно обозначить как F(x) = x3 / 3 + C, где C — любое число.Графикитаких первообразных смещены вертикально относительно друг друга, и их положение зависит отзначенияC.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

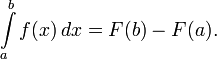
Это соотношение называется формулой Ньютона — Лейбница.

Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:

Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) =F(x) + C для всех x. Число C называютпостоянной интегрирования.

Каждая непрерывная функцияf имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:

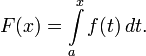
Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, с f(0) = 0 не непрерывна при x = 0, но имеет первообразнуюс F(0) = 0.

Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции(такие какмногочлены,экспоненциальные функции,логарифмы,тригонометрические функции,обратные тригонометрические функциии их комбинации). Например:

Более развёрнутое изложение этих фактов см. в дифференциальной теории Галуа.

Свойства первообразной

Первообразная суммы равна сумме первообразных
Первообразная произведения константы и функции равна произведению константы и первообразной функции
Достаточным условием существования первообразной у заданной на отрезке функции f является непрерывность f на этом отрезке
Необходимыми условиями существования являются принадлежность функции f первому классу Бэраи выполнение для неёсвойства Дарбу
У заданной на отрезке функции любые две первообразные отличаются на постоянную.