Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский кооперативный институт (филиал РУК)

Предмет:

Макроэкономическое планирование и прогнозирование

Файл:

МатАн_ЛинАлг_080100 / Лекции_Математика_3_Интегральное исчисление

.pdf

Скачиваний:

Добавлен:

26.02.2016

Размер:

573.11 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Доказательство. Из вида интеграла следует, что f (x) =1. Тогда при лю-

бом выборе точек ξk	имеем	f (ξk ) = 1, а интегральная сумма равна
n			n		n
∑ f (xk )Dxk = ∑1× Dxk = ∑Dxk = b - a .
k =1			k =1	k =1
Итак, интегральная сумма при любом разбиении отрезка на части и при
любом выборе точек ξk равна b − a . Следовательно,
b			n
∫1× dx =	lim		∑Dxk =	lim	(b - a) = b - a .
a	max xk →0		k =1	max xk	→0
a			k =1
1.2.3.6. Теорема об оценке определенного интеграла
Теорема 17. Если m –		наименьшее, а M – наибольшее значения функции

f (x) на отрезке [a,b] , a < b , то имеет место оценка

m(b - a) £ ∫ f (x)dx £ M (b - a) .

Доказательство. Так как по условию теоремы m ≤ f (x) ≤ M , то по свой-

ству интегрирования неравенств (Теорема 15) получим

∫mdx £ ∫ f (x)dx £ ∫ Mdx .

Применив теперь свойство линейности (Теорема 11), найдем

m∫ dx £ ∫ f (x)dx £ M ∫dx .

Так как ∫dx = (b - a) (Теорема 16), то окончательно получим

m(b - a) £ ∫ f (x)dx £ M (b - a) .

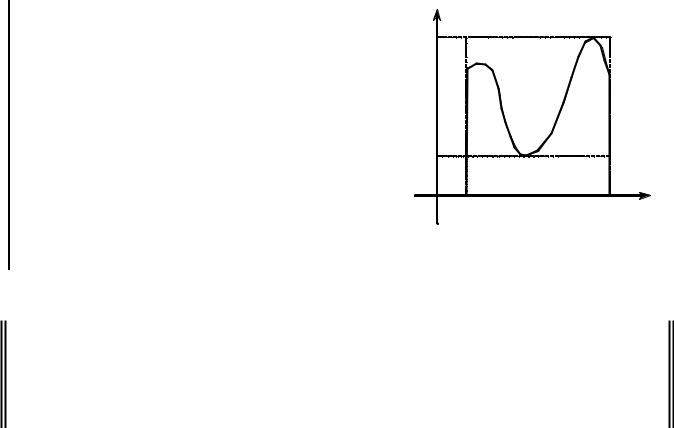
Геометрический смысл теоремы (рис.	y	A2	B2
1.2.5). Если f (x) ³ 0 при x [a,b] , то площадь	M	A2	B2
1.2.5). Если f (x) ³ 0 при x [a,b] , то площадь	M
криволинейной трапеции S f ( x) больше площа-		y = f ( x)
ди прямоугольника aA1B1b и меньше площади		y = f ( x)
ди прямоугольника aA1B1b и меньше площади
прямоугольника aA2 B2b :
SaA1B1b ≤ S f ( x) ≤ SaA2 B2b .	m	A	B1
	m	1	B1
		1
	O a		b	x
		РИС. 1.2.5
1.2.3.7. Теорема о среднем
Теорема 18. Если функция f (x) непрерывна на отрезке [a,b] ,			a < b , то
на этом отрезке существует такая точка c, что выполняется равенство
b
∫ f (x)dx = f (c)(b − a) .
a
Доказательство. Так как функция f (x)	непрерывна на отрезке [a,b] , то

она принимает на этом отрезке свое наименьшее m и наибольшее M значения. Следовательно, в силу теоремы об оценке интеграла (Теорема 17), имеем

m(b − a) ≤ ∫ f (x)dx ≤ M (b − a) .

Отсюда

∫ f (x)dx

m ≤	a			≤ M .

	b − a
Введем обозначение
		b
μ =		∫ f (x)dx
		a			.	(9)

			b − a
Тогда, в силу полученных оценок, число μ удовлетворяет неравенствам
m ≤ μ ≤ M .
По условию теоремы функция			f (x) непрерывна на отрезке [a,b] . Поэто-

му она принимает на этом отрезке все промежуточные значения между m и M. 32

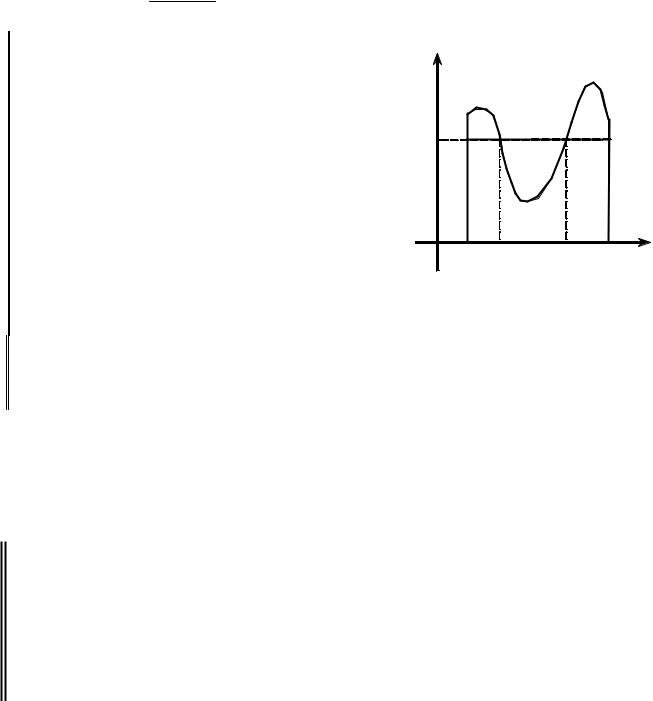
Следовательно, найдется такая точка c [a,b] , в которой						f (c) = μ . Подставляя
это значение μ в равенство (9), получим:
	b
	∫ f (x)dx			b
	a	= f (c) ∫ f (x)dx = f (c)(b − a) .
	b − a	= f (c) ∫ f (x)dx = f (c)(b − a) .
	b − a			a
				a
Геометрический		смысл		теоремы
(рис. 1.2.6).				y			y = f ( x)
(рис. 1.2.6).
Обозначим:
	b			f (c)	A				B
	b			f (c)
1)	∫ f (x)dx = Sкр. трап. –		площадь криво-
	a
линейной трапеции,
2)	f (c)(b − a) = SaABb		– площадь пря-		a	c	с1	b	x
				O	a	c	с1	b	x
моугольника aABb с основанием b − a и вы-						РИС. 1.2.6
сотой f (c) .						РИС. 1.2.6
сотой f (c) .
Тогда доказанная теорема утверждает, что существует точка c [a,b] , для
которой				Sкр. трап. = SaABb .
				Sкр. трап. = SaABb .

Точка c необязательно будет единственна. Так для функции y = f (x) ,

представленной на рис. 1.2.6, таких точек две: c и c1.

С доказанной выше теоремой связано очень важное и имеющее многочисленные приложения понятие среднего значения функции.

Средним значением yср функции		y = f (x) , непрерывной на отрезке
[a,b] , называется величина
	b
y =	∫ f (x)dx
	a		.
	b − a		.
ср

Понятие среднего значения функции очень часто употребляется в физике, механике, технике и т.д. Многие величины часто характеризуются своими средними значениями. Например, давление пара, сила и напряжение переменного тока, скорость химической реакции и многие другие.

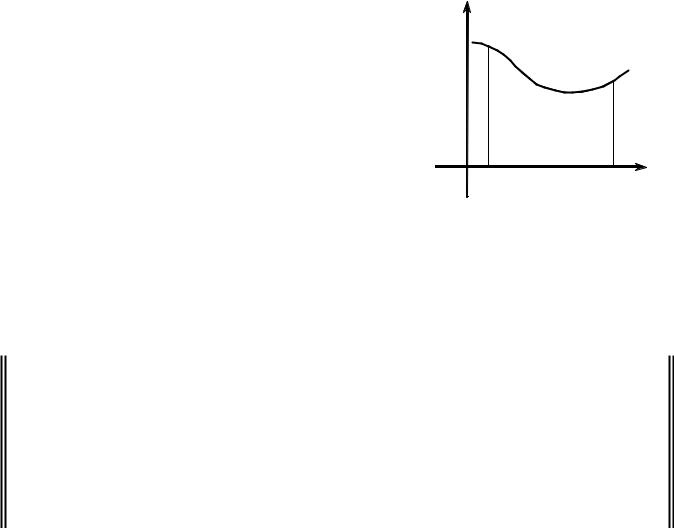
1.2.4.Вычисление определенного интеграла

1.2.4.1.Интеграл с переменным верхним пределом

Рассмотрим определенный интеграл ∫ f (x)dx .

Пусть a – фиксированное число, а b – переменная величина. личным значениям b будут соответствовать различные значения следовательно, интеграл есть функция верхнего предела.

Обозначив верхний предел интегрирования	y
через x, а переменную интегрирования через t,	A
через x, а переменную интегрирования через t,
получим функцию

Тогда разинтеграла,

Φ(x) = ∫ f (t)dt .

Если f (t) ³ 0 , то F(x) – площадь криволи- O a	x t
нейной трапеции aAXx (рис. 1.2.7) с переменным	РИС. 1.2.7
основанием [a, x] .

1.2.4.2. Теорема о производной интеграла с переменным верхним преде-

лом

Теорема. Если f (x) – непрерывная функция, то

′	x	¢
′	∫		= f (x) ,
Φ (x) =		f (t)dt	= f (x) ,
	a

то есть производная интеграла по переменному верхнему пределу равна подынтегральной функции.

Доказательство. Найдем производную Φ′( x) по шагам.

1. Дадим аргументу x приращение x и вычислим значение функции в точке x + x :

x+Δx	x	x+Δx	x+Δx
Φ ( x + x) = ∫ f (t)dt = ∫ f (t)dt + ∫ f (t)dt = Φ(x) + ∫ f (t)dt .
a	a	x	x

Здесь использовано свойство аддитивности.

2. Найдем приращение функции

x+Δx	x+Δx
ΔΦ = Φ(x + x) − Φ(x) = Φ(x) + ∫ f (t)dt − Φ(x) = ∫ f (t)dt .
x	x
К полученному интегралу применим теорему о среднем, в силу которой
существует такая точка с, заключенная между x и x +	x , что
x+Δx

ΔΦ = ∫ f (t)dt = f (c)(x + x − x) = f (c) x .

3. Найдем отношение

ΔΦ = f (c) x =

f (c) .

4.Вычислим предел при x → 0 и найдем производную

Φ′(x) = lim ΔΦ = lim f (c) .
	x→0 x		x→0
Так как точка с заключена между x и x +				x и	x → 0 , то c → x . Оконча-
тельно, в силу непрерывности	f (x) , имеем
Φ′(x) = lim	f (c) = lim f (c) = f (x) .
x→0		c→x
Из доказанной теоремы следует, что всякая непрерывная функция имеет
первообразную.
Действительно, в силу теоремы существования определенного интеграла
для всякой непрерывной функции		f (x) существует интеграл
		x
Φ(x) = ∫ f (t)dt .
		a
Но так как по доказанному		Φ′(x) = f (x),		то	Φ(x) – первообразная для
функции f (x) .
1.2.4.3. Формула Ньютона-Лейбница
Теорема. Если F(x) –	какая-то		первообразная непрерывной функции
f (x) , то справедлива формула

∫ f (x)dx = F (b) − F (a).

Эта формула называется формулой Ньютона– Лейбница.

Доказательство. Функция F(x) – заданная первообразная для функции f (x) . По теореме о производной интеграла с переменным верхним пределом

функция Φ(x) = ∫ f (t)dt также является первообразной для f (x) . Но так как

две первообразные одной и той же функции отличаются друг от друга на постоянную, то

F (x) = Φ(x) + C .

Тогда

F(b) − F (a) = (Φ(b) + C ) − (Φ(a) + C ) = Φ(b) − Φ(a) =

b	a	b
= ∫ f (t)dt − ∫ f (t)dt = ∫ f (t)dt .
a	a	a

Вернемся теперь к обычному обозначению переменной интегрирования через x. Окончательно получим

∫ f (x)dx = F (b) − F (a) .

Введем знак «двойной подстановки»:

F (x) |ba = F (b) − F (a) .

Тогда формулу Ньютона– Лейбница можно записать в виде

∫ f (x)dx = F (x) |ba = F (b) − F (a) .

Эта формула используется для вычисления определенного интеграла

∫ f (x)dx . Сначала находится первообразная F (x) для подынтегральной функ-

ции f (x) (эта задача была решена в Разделе I), а затем вычисляется разность

F (b) − F (a) .

Примеры.

2	x4	2	24		1		15

1. ∫ x3dx =		=		−		=		.
	4
1		4		4		4
		1

1		xdx		1	1	2xdx		1	1 d (1 + x2 )				1

2. ∫			=		∫		=		∫		=	1 + x2

	1 + x2			2		1 + x2		2		+ x2
0					0				0 1				0

= 2 − 1.

1.2.5. Замена переменной в определенном интеграле

Теорема 19. Пусть дан

∫ f (x)dx ,

где f (x) – непрерывная на [ a,b ] функция. Пусть x = ϕ(t) , причем ϕ(t) удовле-

творяет условиям:

1) ϕ(t) , ϕ′(t) непрерывны на [ α,β ], 2) ϕ(α) = a , ϕ(β) = b .

Тогда имеет место формула

b	β
∫ f (x)dx = ∫ f [ϕ(t)]ϕ′(t)dt .		(10)
a	α
Доказательство. Из условий теоремы и свойств непрерывных функций
следует, что обе подынтегральные функции из формулы (10) непрерывны:		f (x)
– непрерывна на [ a,b ], f [ϕ(t)]ϕ′(t) –	непрерывна на [ α,β ]. Следовательно, ин-

тегралы в формуле (10) существуют. Покажем, что они равны одному значению.

Если F (x) – первообразная для f (x) , т.е.

∫ f (x)dx = F (x) + C ,

то по формуле Ньютона-Лейбница имеем

∫ f (x)dx = F (x) ba = F (b) − F (a) .

Так как ∫ f [ϕ(t)]ϕ′(t)dt = ∫ f [ϕ(t)]d[ϕ(t)] = F[ϕ(t)] + C (свойство инвари-

антности формул интегрирования), то F[ϕ(t)] – первообразная для f [ϕ(t)]ϕ′(t) .

Следовательно,

∫ f [ϕ(t)]ϕ′(t)dt = F[ϕ(t)] |βα = F[ϕ(β)] − F[ϕ(α)] = F (b) − F (a) .

Сравним доказанную формулу (10) с формулой (2) замены переменной в неопределенном интеграле. Подынтегральные функции в этих формулах совпадают, отличия состоят в следующем:

в определенном интеграле обязательна смена пределов интегрирования по

формулам ϕ(α) = a ,

ϕ(β) = b ;

после вычисления неопределенного интеграла необходимо вернуться к

старой переменной, в определенном интеграле этого делать не нужно.

Примеры.

1. Найти ∫

1 +

Решение. Положим x = t

2 ,

dx = 2tdt ,

= 0 t

= 0 ,

= 4 t

= 2 . То-

гда

2tdt

∫

= 2∫ 1 −

dt = 2(t

0 − ln

t + 1

0 ) = 4

− 2ln 3.

1 + t

+ x

1 + t

1 − x2

2. Найти

∫

dx .

t = π ,

= π .

Решение. Положим x = sin t,

dx = costdt,

x = 1 t

Тогда

1 − x2

1 − sin2 t

2 cos2 t

∫

dx = ∫

costdt

∫

dt =

sin

π sin

1 − sin2 t

= ∫

dt = ∫

−

1 dt = − ctg t

π2

− t

π2 = 1 −

sin

1.2.6. Интегрирование по частям в определенном интеграле

Теорема 20. Если u(x) , v(x) , u′(x) , v′( x) ,

–

непрерывны на отрезке [ a,b

], то имеет место формула

b	b
∫udv = uv \|ba −∫vdu ,		(11)
a	a

которая называется формулой интегрирования по частям в определенном интеграле.

Доказательство. В силу предположений теоремы, интегралы в доказываемой формуле (11) существуют. Кроме того, заметим, что формулу Ньютона – Лейбница можно записать в виде

b		= (∫ f (x)dx)	b .
∫ f (x)dx = F (x)	ba


a			a

Используя это соображение и формулу интегрирования по частям для неопределенного интеграла, получим

∫udv = (∫udv)

b = (uv − ∫vdu )

b = uv

ba − (∫vdu )

= uv

ba − ∫vdu .

Пример.

Найти ∫ x cos xdx .

Решение. Пусть u = x ,

du = dx ,

dv = cos xdx ,

v = sin x .

π − 1.

∫ x cos xdx = x sin x

− ∫sin xdx = x sin x

02 + cos x

02 =

1.3.Приложения определенного интеграла

1.3.1.Вычисление площади криволинейной трапеции

Вычисление площадей плоских фигур основано на геометрическом смыс-

b
ле определенного интеграла: если f (x) ³ 0 на [a,b], то ∫ f (x)dx –	это площадь
a
криволинейной трапеции, ограниченной сверху кривой y = f (x) ,	и имеющей в
основании отрезок [a,b].

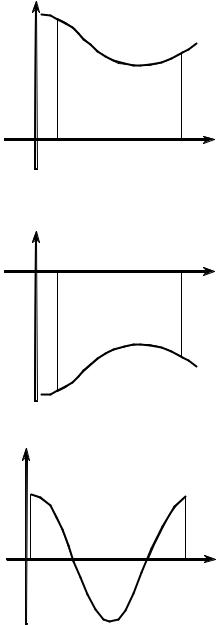
В этом пункте рассмотрим различные случаи расположения криволинейной трапеции, которая определяется основанием и кривой y = f (x) . Найдем ее

площадь в каждом случае.
1. Основание	x [a,b] ,	f (x) ³ 0 на [a,b]
		y			y = f ( x)
(рис. 1.3.1).					y = f ( x)
(рис. 1.3.1).
b
Тогда ∫ f (x)dx ³ 0 . В силу геометрического
Тогда ∫ f (x)dx ³ 0 . В силу геометрического					+
a

смысла интеграла	площадь	S криволинейной
		O	a			b x
		b
трапеции вычисляется по формуле S = ∫ f (x)dx .				РИС. 1.3.1

2. Основание x Î[a,b] ,		f (x) ≤ 0 на [a,b]
(рис. 1.3.2).
	b
Тогда	∫ f (x)dx £ 0 .	Следовательно,

S = -∫ f (x)dx .

3. Основание x Î[a,b] , f (x) меняет знак на

[a,b] (рис. 1.3.3).

Интеграл ∫ f (x)dx разбиваем на сумму ин-

тегралов

y
a		b
O	¾	x
	¾

y = f ( x)

РИС. 1.3.2

+	y = f ( x)
		+

O a c	−	d b x

РИС. 1.3.3

b	c	d	b
∫ f (x)dx = ∫ f (x)dx + ∫ f (x)dx + ∫ f (x)dx .
a	a	c	d
c	d		b
Здесь ∫ f (x)dx ³ 0,	∫ f (x)dx £ 0,		∫ f (x)dx ³ 0.
a	c		d

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в папке МатАн_ЛинАлг_080100

#
26.02.2016483.32 Кб41ЗаданияСР_ЛА_080100.pdf
#
26.02.2016690.03 Кб41ЗаданияСР_МА_080100.pdf
#
26.02.2016869.89 Кб49ЛА_экз_1курс_экономика_заочн.doc
#
26.02.2016454.39 Кб44Лекции_Математика_1_Линейная_алгебра.pdf
#
26.02.2016494.69 Кб51Лекции_Математика_2_Дифференциальное исчисление.pdf
#
26.02.2016573.11 Кб48Лекции_Математика_3_Интегральное исчисление.pdf
#
26.02.20161.52 Mб59МА_экз_1курс_экономика_заочн.doc
#
26.02.2016855.38 Кб43Математика_Словарь терминов.pdf
#
26.02.2016630.28 Кб47ПланыПЗ_ЛА_080100.pdf
#
26.02.2016496.78 Кб56ПланыПЗ_МА_080100.pdf