Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский кооперативный институт (филиал РУК)

Предмет:

Макроэкономическое планирование и прогнозирование

Файл:

МатАн_ЛинАлг_080100 / Лекции_Математика_3_Интегральное исчисление

.pdf

Скачиваний:

Добавлен:

26.02.2016

Размер:

573.11 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

c d b

Следовательно, S = ∫ f (x)dx − ∫ f (x)dx + ∫ f (x)dx .

a c d

4. Основание x [a,b] ,
		1				[	a,c	]	,
	f (x), x						a,c		,
f (x) =			2	(x), x [c,b],
		f	2
		f

(рис. 1.3.4).
Используя свойство аддитивности инте-
грала, получим
c	d
S = ∫ f1 (x)dx + ∫ f2 (x)dx .
a	c
5. Основание y [c, d ]					на оси Oy, кривая,
ограничивающая	трапецию,						имеет уравнение

x = ϕ( y) (рис. 1.3.5).

Тогда S = ∫ϕ( y)dy .

Примеры.

y	(x)
y = f 2

y = f1 ( x)

a с

b x

РИС. 1.3.4

y d

x = ϕ( y)

с
O	x

РИС. 1.3.5

1. Найти площадь S криволинейной трапеции, ограниченной линиями: y = x3 ,

y = 0 , x = −1, x = 1.

Решение.

Построим чертеж (рис. 1.3.6). Так как

∫ x3dx ≤ 0 , то

−1
			0			1
S = − ∫ x3dx + ∫ x3dx =
		−1				0
= −	x4	0	+	x4	1	=	1	+	1	=	1	.


	4	−1	4		0	4 4 2

2. Найти S криволинейной трапеции,
ограниченной линиями:						y = x + 1, y = cos x ,

y = 0 .

Решение.

Построим плоскую фигуру (рис. 1.3.7). Тогда искомая площадь будет суммой двух интегралов

0 π/2

S = ∫ (x + 1)dx + ∫ cos xdx =

−1 0

=	(x + 1)2	0	+ sin x	π/2	=	3	.


				0
2		−1			2

	y
		y = x 3
-1		+
-1
—	O	1 x
	O

РИС. 1.3.6

y y = x + 1

y = cos x

-1 O	π	x

РИС. 1.3.7

1.3.2. Вычисление площадей плоских фигур

Рассмотрим плоскую фигуру, ограниченную линиями y = f1 (x) , y = f2 (x)

и прямыми x = a , x = b . Пусть f1 ( x) ≤ f2 (x) на отрезке [ a,b ]. Требуется найти площадь этой фигуры.

В случае 0 ≤ f1 (x) ≤ f2 (x) из рис. 1.3.8 видно, что площадь фигуры вычис-

ляется как разность площадей двух криволинейных трапеций

	b		2		b	1	b		2	1	]
S =	∫	f	2	(x)dx −	∫	1	∫[	f	2	1	]
S =		f		(x)dx −		f (x)dx =		f		(x) − f (x) dx .
	a				a		a
										y
y											y = f 2 (x)
y = f 2 ( x)

		O	a	y = f1	( x)
				y = f1	( x)
	y = f1 ( x)
O a	b x	-M
	РИС. 1.3.8			РИС. 1.3.9

(12)

Покажем, что формула (12) верна при любом расположении линий y = f1 (x) , y = f2 (x) относительно оси Oy (рис. 1.3.9).

Действительно, сделаем параллельный перенос оси Ox вниз на величину −M . Получим новую систему координат XOY, где X = x , Y = y + M . Число M

подберем так, чтобы уравнения кривых в новой системе координат удовлетворяли условиям:

		Y = F1 (x) , F1 ( x) = f1 (x) + M ³ 0 ;
	Y = F2 (x) , F2 (x) = f2 (x) + M ³ 0 ;
причем F1 (x) £ F2 ( x) .
Тогда площадь фигуры равна
	b	2	1	b	[		2		1	]
S =	∫	2	1	∫	[	f	2	(x) −	1	]
S =		[F	(x) − F (x)]dx =			f		(x) −	f	(x) dx.
	a			a

Пример.

Найти площадь фигуры, ограниченной ли-

ниями x = 4 ,	y = − x ,			y = x2 .			y
ниями x = 4 ,	y = − x ,			y = x2 .
Решение.							y = x2
							y = x2
Построим чертеж (рис. 1.3.10). Тогда
		4
				2	+		O	4 x
		S = ∫ x			+	x dx =	O	4 x
		0					y = −	x
	3	+ 2 x	3		4	= 64 + 16	РИС. 1.3.10
= x		+ 2 x				= 64 + 16	= 80 .
3		3				3 3	3
					0

1.3.3.Вычисление длин дуг

1.3.3.1.Определение длины дуги плоской кривой


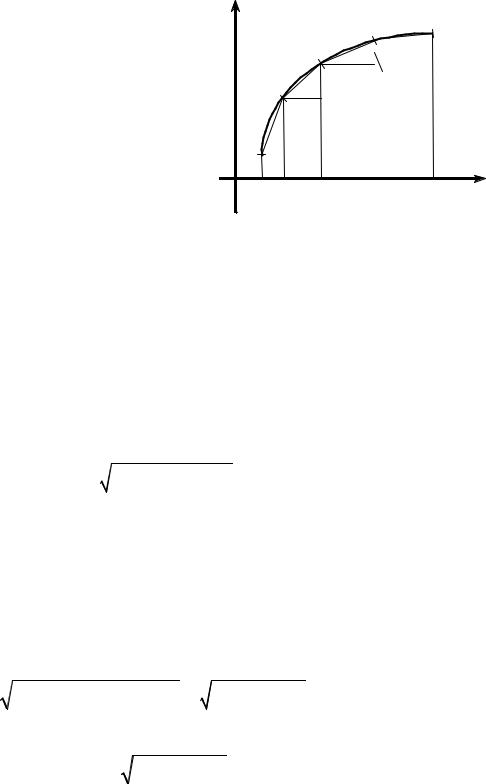
Пусть MN – дуга некоторой плоской кривой		N
		N

(рис. 1.3.11). Впишем в дугу MN произвольную ло-		lk
		lk
маную линию. Обозначим длины ее звеньев через	l1 ,
n		M
n
l2 , ..., ln . Длина ломаной линии равна ∑ lk .		РИС. 1.3.11

k =1

Длиной l дуги называется предел периметра вписанной в нее ломаной линии, когда число звеньев неограниченно растет, а длина максимального звена стремится к нулю

	n
l = lim	∑ lk .
max lk →0	k =1
	k =1

1.3.3.2. Длина дуги в прямоугольных координатах

Постановка

задачи. Пусть

кривая

M k

задана уравнением

y = f (x) .

Предполо-

M k −1

жим, что f (x) и

f ′(x) непрерывны на от-

резке [a,b] . Требуется найти длину дуги

MN кривой y = f (x) на отрезке [a,b] (рис.

1.3.12).

O x0=a x1

xk-1

xn=b

Решение задачи.

РИС. 1.3.12

Разобьем дугу

MN на n частей точками M0 ( x0 , f (x0 )) = M , M1 ( x1, f (x1)) ,

M2 ( x2 , f (x2 )) , ...,

Mn ( xn , f (xn )) = N . Соединим эти точки отрезками прямых.

Обозначим длины зве-

В результате получим ломаную, вписанную в дугу MN .

ньев ломаной через lk , k =

, а их проекции на оси Ox и Oy через

1,n

xk ,

yk ,

k =

, соответственно, причем

= f ( xk ) − f (xk −1 ) . Тогда

1,n

( x )2 + ( y

)2 .

Воспользуемся

теоремой

Лагранжа,

по которой на

каждом

отрезке

[xk −1 , xk ] существует точка ξk , в которой выполняется равенство

или

f (xk ) − f ( xk −1 ) = f ′(ξk )(xk − xk −1 )

yk = f ′(ξk ) xk .

Тогда длина k-го звена ломаной отыщется по формуле

l =

( x )2 + [ f

′(ξ

) x ]2

1 + [ f ′(ξ

)]2

x ,

а длина всей ломаной равна

∑ lk =

∑ 1 + [ f ′(ξk )]2 xk .

k =1

Полученная сумма является интегральной. Найдем предел последовательности этих сумм, когда max lk → 0 . Учитывая, что при стремлении max lk к

нулю величина max xk также стремится к нулю, получим

					n
					n
	l = lim				∑ 1 + [ f ′(ξk )]2 xk =
		max l		→0	k =1
			k		k =1
			k
		n				b
= lim	→0	∑ 1 + [ f ′(ξk )]2				xk = ∫ 1 + [ f ′(x)]2 dx .
max xk	→0	k =1				a
		k =1				a

Таким образом, если кривая задана уравнением y = f (x) , то длина ее дуги на отрезке x [a,b] вычисляется по формуле

							b
						l = ∫ 1 + [ f ′(x)]2 dx .												(13)
							a
Найти длину дуги цепной линии y =												ex	+ e− x		на отрезке x [0, a] .
Найти длину дуги цепной линии y =													2		на отрезке x [0, a] .
													2
Решение.
Так как y′ =	ex − e− x					, то
Так как y′ =		2				, то
		2
				ex − e− x 2							e2 x		− 2ex e− x + e−2 x
1 + y′2 = 1 +								= 1 +											=
1 + y′2 = 1 +					2			= 1 +						4					=
					2									4
	=		e2 x		+ 2ex e− x + e−2 x					=		ex + e− x 2
																	.
							4						2				.
							4						2
Тогда
a						a ex	+ e− x			ex			− e− x			a		ea − e−a


l = ∫ 1 + y′2 dx = ∫									dx =							=				.
l = ∫ 1 + y′2 dx = ∫							2		dx =				2			=		2		.
0					0		2						2			0		2
0					0											0

Формулу (13) для длины дуги можно преобразовать следующим образом:

b b

l = ∫ 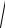(dx)2 + [ f ′(x)dx]2 = ∫ 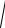(dx)2 + (dy)2 .

a a

Если теперь также заменить пределы интегрирования a и b на точки M и N

– начало и конец дуги, то получим другую форму записи формулы (13):

N
l = ∫ (dx)2 + (dy)2 .	(14)

1.3.4.Вычисление объемов тел

1.3.4.1.Вычисление объемов тел по площадям параллельных сечений

Постановка задачи. Пусть дано не-
которое тело T. Предположим, что извест-
на площадь любого сечения этого тела		y
плоскостью, перпендикулярной	оси Ox		T
(рис. 1.3.13). Эта площадь зависит от по-
ложения секущей плоскости и,	следова-	O
тельно, является функцией переменной x:		O	x	b	x
тельно, является функцией переменной x:		a	x	b	x
S = S(x) , x [a,b] (отрезок [a,b]	– проек-	z
ция тела T на ось Ox). Требуется найти			РИС. 1.3.13
объем тела T.
Решение задачи.
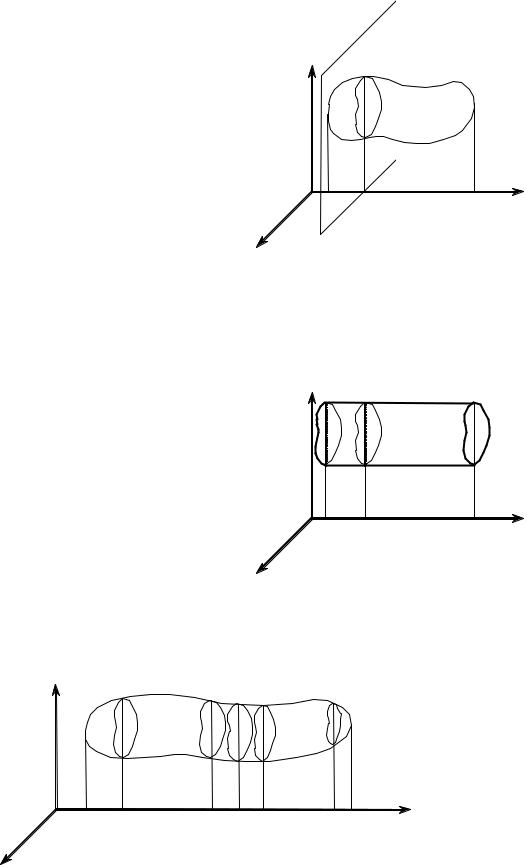
1. Частный случай (рис. 1.3.14).
Пусть тело T – прямой цилиндр с направ-		y
ляющей, параллельной оси x. Тогда пло-			T
щадь поперечного сечения такого тела бу-
дет постоянной величиной при любых зна-		O a
чениях x ( S (x) = S = const ), а его объем		O a	x	b	x
найдется как произведение площади осно-		z
найдется как произведение площади осно-
вания S на высоту h = b - a , то есть			РИС. 1.3.14

V= S × h = S (b - a) .

2.Общий случай (рис. 1.3.15).

O	xk-1 ξk xk
x0=a x1	xk-1 ξk xk	xn-1 xn=b x

РИС. 1.3.15

Разобьем тело произвольно на n частей (слоев) плоскостями, перпендику-


лярными оси Ox и проходящими через точки x0 = a ,				x1 ,		x2 , ..., xn = b . Обозна-
чим длины полученных отрезков [xk −1 , xk ], k =			через
		1,n				xk .
Выберем произвольно точки ξk [xk −1 , xk ], k =					и проведем через них
				1,n
сечения, площади которых равны Sk	= S (ξk ) .
Найдем объем Vk каждого k-го слоя приближенно,							считая его прямым
цилиндром с площадью основания S (ξk ) и высотой				xk :		Vk	≈ S (ξk ) xk .
Тогда для объема всего тела имеем приближенную формулу
n	n
V = ∑Vk ≈	∑S (ξk ) xk .
k =1	k =1
Полученная сумма является	интегральной.			Перейдя к пределу при

стремлении max xk → 0 получим точную формулу для вычисления объема тела

						n
		V =	lim		→0	∑ S (ξk ) xk .
			max	x	→0	k =1
				k		k =1
				k
Если теперь вспомнить определение определенного интеграла, то оконча-
тельно получим, что объем V тела T с известной площадью S(x)									поперечных
сечений находится по формуле
					b
			V = ∫ S (x)dx .						(15)
					a
							y
Найти объем тела, ограниченного эллиптиче-
ским параболоидом z2	+	y2	= x	и плоскостью x = 1.			O	x	1 x
2		8					O	x	1 x
2		8

Решение. Построим чертеж (рис. 1.3.16).

РИС. 1.3.16

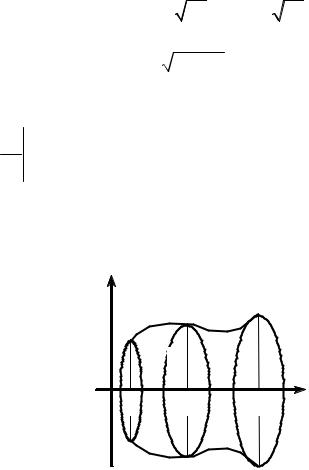
В сечении тела плоскостью, перпендикулярной оси Ox, получим плоскую

	z2	+	y2	= 1 с полуосями a =		и b = 2		.
фигуру, ограниченную эллипсом					2x		2x
	2x		8x

Площадь этой фигуры вычисляется по формуле S = pab = p22x × 2x = 4px . Тогда

1	1		1
V = ∫ S (x)dx = 4p∫ xdx = 4p x2			= 2p (куб.ед.).
0	0	2	0
0	0		0
1.3.4.2. Вычисление объемов тел вращения
Постановка задачи. Пусть криволинейная
трапеция с основанием [a,b] ,	ограниченная кри- y				y = f ( x)
вой y = f (x) вращается вокруг оси		Ox	(рис.		y = f ( x)
вой y = f (x) вращается вокруг оси		Ox	(рис.
1.3.17). Найти объем полученного тела вращения.					y
					y
Решение задачи. Рассмотрим сечение тела				O a	x	b	x
плоскостью, проходящей через точку		x оси Ox,		O a	x	b	x
плоскостью, проходящей через точку		x оси Ox,
перпендикулярно этой оси. В таком сечении тела
вращения получается круг	радиуса	R = f (x) .

РИС. 1.3.17

Следовательно, его площадь равна

S (x) = πR2 = π[ f ( x)]2 .

Используя формулу (15), для объема тела по известным площадям параллельных сечений, получим:

V = p∫[ f (x)]2 dx –

объем тела вращения криволинейной трапеции с основанием [a,b] , ограни-

ченной графиком функции y = f (x) .

									y
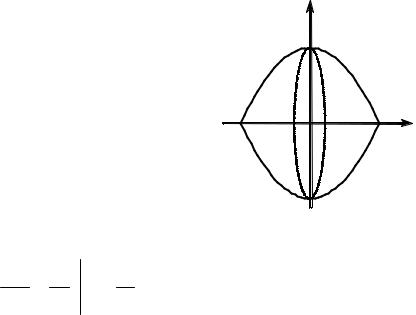
Найти объем тела,	образованного вращением								1	y = 1− x 2
вокруг оси Ox кривой y = 1 − x2			на отрезке x [−1,1].
Решение. Построим чертеж (рис. 1.3.18). Из
него видно, что								-1	O	1 x
него видно, что
1		1
V = π ∫ (1 − x2 )2 dx = π ∫ (1 − 2x2 + x4 )dx =
−1		−1							РИС. 1.3.18
									РИС. 1.3.18
	−	2x3	+	x5	1	=	16	π (куб.ед.).
= π x	−	3	+	5		=	15	π (куб.ед.).
		3		5	−1		15

1.4.Несобственные интегралы

1.4.1.Понятие несобственных интегралов

При введении понятия определенного интеграла ∫ f (x)dx считалось, что

отрезок [a,b] конечный, а функция f (x) непрерывна на [a,b] и, следовательно,

ограничена. Если нарушено хотя бы одно из перечисленных условий, то определить интеграл, как предел последовательности интегральных сумм нельзя. Однако имеется другой способ обобщить понятие определенного интеграла на случаи, когда:

1)интервал интегрирования бесконечный,

2)подынтегральная функция неограниченная.

Такие интегралы называются несобственными интегралами.

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Соседние файлы в папке МатАн_ЛинАлг_080100

#
26.02.2016483.32 Кб41ЗаданияСР_ЛА_080100.pdf
#
26.02.2016690.03 Кб41ЗаданияСР_МА_080100.pdf
#
26.02.2016869.89 Кб49ЛА_экз_1курс_экономика_заочн.doc
#
26.02.2016454.39 Кб44Лекции_Математика_1_Линейная_алгебра.pdf
#
26.02.2016494.69 Кб51Лекции_Математика_2_Дифференциальное исчисление.pdf
#
26.02.2016573.11 Кб48Лекции_Математика_3_Интегральное исчисление.pdf
#
26.02.20161.52 Mб59МА_экз_1курс_экономика_заочн.doc
#
26.02.2016855.38 Кб43Математика_Словарь терминов.pdf
#
26.02.2016630.28 Кб47ПланыПЗ_ЛА_080100.pdf
#
26.02.2016496.78 Кб56ПланыПЗ_МА_080100.pdf