
080100Экономика(МатАнализ и ЛинАлгебра) / Математический анализ_080100_заоч_1_курс_экз_паспорт
.pdfАВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ЦЕНТРОСОЮЗА РОССИЙСКОЙ ФЕДЕРАЦИИ «РОССИЙСКИЙ УНИВЕРСИТЕТ КООПЕРАЦИИ»
КАЗАНСКИЙ КООПЕРАТИВНЫЙ ИНСТИТУТ (ФИЛИАЛ)
УТВЕРЖДАЮ Проректор по учебной работе
Казанского кооперативного института (филиала) Российского университета кооперации
_____________А. М. Хуснутдинова «____»_________________20___г.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ТЕСТОВЫЕ ЗАДАНИЯ
Направление подготовки (специальность) 080100.62 «Экономика»
Составители: ________________________________А.В. Поташев
________________________________Е.В. Поташева
«___»_____________2013 г.
Тестовые задания обсуждены на заседании кафедры «Инженернотехнические дисциплины и сервис» «__»____________2013 г., протокол №__.
Заведующий кафедрой ___________________________ А.М. Мухаметшин
СОГЛАСОВАНО Начальник отдела менеджмента качества _______________ Д.Н. Алюшева
1
№ |
Наименование пункта |
Значение |
1. |
Кафедра |
Инженерно-технические |
|
|
дисциплины и сервис |
2. |
Автор – разработчик |
Поташев А.В., д.ф.-м.н., профессор |
|
|
Поташева Е.В., к.т.н., доцент |
3. |
Наименование дисциплины |
Математический анализ |
|
|
|
4. |
Общая трудоемкость по |
216 (1 курс) |
|
учебному плану |
|
5. |
Вид контроля (нужное |
Предварительный (входной), |
|
подчеркнуть) |
текущий, промежуточный |
|
|
(экзамен) |
6. |
Для специальности(ей)/ |
080100.62 «Экономика» |
|
направления(й) подготовки |
нормативный срок и СПО |
|
|
заочная форма обучения |
7. |
Количество тестовых |
|
|
заданий всего по дисциплине, |
432 |
|
из них |
|
8. |
Количество заданий при |
24 |
|
тестировании студента |
|
|
|
|
9. |
Из них правильных ответов |
|
|
(в %): |
|
10. |
для оценки «отлично» |
85 % и больше |
|
|
|
11. |
для оценки «хорошо» |
70 % - 85% |
|
|
|
12. |
для оценки |
50% - 70% |
|
«удовлетворительно» |
|
|
или для получения оценки |
- |
|
«зачет» не менее |
|
13. |
Время тестирования (в |
45 |
|
минутах) |
|
2
Содержание |
|
|
Стр. |
V1: ЭЛЕМЕНТЫ ТЕОРИИ ПРЕДЕЛОВ .............................................................. |
4 |
V2: Элементы теории множеств........................................................................ |
4 |
V2: Понятие функции ......................................................................................... |
7 |
V2: Предел на бесконечности.......................................................................... |
10 |
V2: Предел функции в точке............................................................................ |
12 |
V2: Замечательные пределы............................................................................. |
16 |
V2: Непрерывность функции, точки разрыва ................................................ |
20 |
V2: Асимптоты графика функции................................................................... |
28 |
V1: ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ |
|
ПЕРЕМЕННОЙ ..................................................................................................... |
32 |
V2: Геометрический и физический смысл производной .............................. |
32 |
V2: Производные первого порядка ................................................................. |
38 |
V2: Производные высших порядков............................................................... |
42 |
V2: Приложения дифференциального исчисления ФОП. ............................ |
43 |
V1: ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ |
|
ПЕРЕМЕННЫХ..................................................................................................... |
49 |
V2: Частные производные первого порядка................................................... |
49 |
V2: Частные производные высших порядков ................................................ |
54 |
V2: Полный дифференциал, производная по направлению, градиент........ |
57 |
V1: ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ .............................................................. |
61 |
V2: Основные методы интегрирования .......................................................... |
61 |
V2: Методы вычисления определенного интеграла...................................... |
65 |
V2: Приложения определенного интеграла.................................................... |
66 |
V2: Несобственные интегралы ........................................................................ |
70 |
V1: ЭЛЕМЕНТЫ ТЕОРИИ РЯДОВ.................................................................... |
73 |
V2: Сходимость числовых рядов..................................................................... |
73 |
V2: Область сходимости степенного ряда...................................................... |
80 |
V2: Ряд Тейлора (Маклорена) .......................................................................... |
83 |
V1: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.................................................... |
86 |
V2: Типы дифференциальных уравнений. ..................................................... |
86 |
V2: Дифференциальные уравнения первого порядка. .................................. |
90 |
V2: Дифференциальные уравнения высших порядков................................. |
93 |
3
F1: Математический анализ экзамен 1 курс 2013/2014 F2: Поташев А.В., Поташева Е.В.
F3: Тестовые задания по направлению подготовки 080100.62 «Экономика» заочная нормативный срок и СПО 432 заданий, 24 вопроса, 216 часов
F4: Дидактическая единица; Раздел; Тема
V1: Элементы теории пределов
V2: Элементы теории множеств
I:
S: Установить соответствия между списками двух множеств, заданных различным образом:
L1: 
L2: 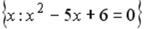
L3: 
L4:  R1:
R1: 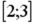
R2: 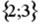
R3: 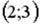
R4: 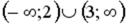
R5: 
I:
S: Установить соответствия между списками двух множеств, заданных различным образом:
L1: 
L2: 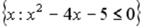
L3: 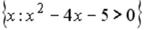
L4: 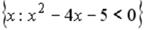 R1:
R1: 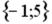
R3: 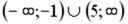
R5: 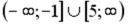
R2: 
R4: (-1; 5)
I:
S: Установите соответствие между заданными числами и множествами, которым они принадлежат.
L1: 
L2:  L3:
L3: 
4
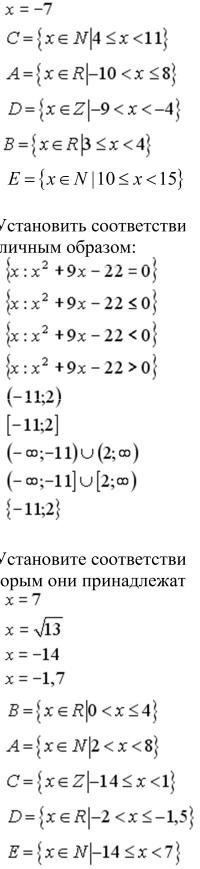
L4: |
|
R3: |
|
R1: |
|
R4: |
|
R2: |
|
R5: |
|
I: |
|
S: |
между списками двух множеств, заданных |
L1: |
|
L2: |
|
L3: |
|
L4: |
|
R3: |
|
R2: |
|
R4: |
|
R5: |
|
R1: |
|
I: |
|
S: |
между заданными числами и множествами, |
|
. |
L1: |
|
L2: |
|
L3: |
|
L4: |
|
R2: |
|
R1: |
|
R3: |
|
R4: |
|
R5: |
|
I: |
|
5
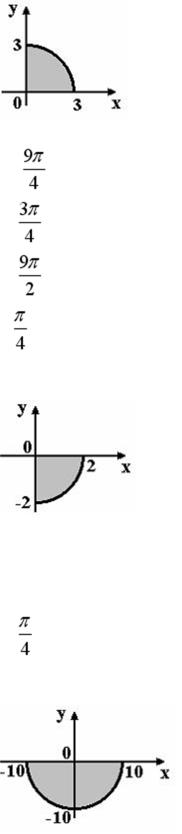
S: Мера множества, изображенного на рисунке,
равна…
+:
-:
-:
-:
I:
S: Мера множества, изображенного на рисунке,
равна…
-:  -:
-: 
+: 
-:
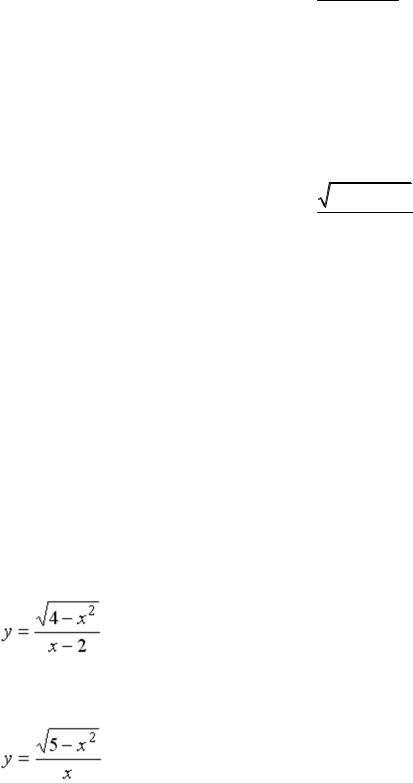
I:
S: Мера множества, изображенного на рисунке,
равна…
-:  -:
-:  +:
+: 
6

-: 
I:
S: Мера множества, изображенного на рисунке,
равна…
+:  -:
-:  -:
-:  -:
-: 
V2: Понятие функции
I:
S: Областью определения функции у = |
2x - 4 |
является множество точек вида |
||||||
|
||||||||
|
|
|
|
|
|
|
3x - 2 |
|
|
|
|
2 |
|||||
+: |
A = x : x ¹ |
|
|
|
|
|
||
|
|
|
|
|||||
|
|
|
3 |
|||||
|
|
3 |
||||||
-: |
B = x : x ¹ |
|
|
|
|
|||
|
|
|||||||
|
|
2 |
||||||
|
|
2 |
||||||
-: |
C = x : x ³ |
|
|
|
|
|||
|
|
|||||||
|
|
3 |
||||||
|
|
2 |
||||||
-: |
D = x : x £ |
|
|
|
|
|||
|
|
|
||||||
|
|
3 |
||||||
I: |
|
|
|
|
|
|
|
|
|
S: Областью определения функции у = |
|
|
− |
|
|
|
является множество |
||
x − 3 |
x + 3 |
||||||||
точек вида |
|
|
|
|
|
|
|
|
|
-: A = {x Î(-¥, -3) È[3,¥)} |
|
|
|
|
|
|
|
|
|
-: B = {x Î[-3,¥)} |
|
|
|
|
|
|
|
|
|
+: C = {x Î[3,¥)} |
|
|
|
|
|
|
|
|
|
-: D = {x Î[-3,3]} |
|
|
|
|
|
|
|
|
|
I: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
S: Областью определения функции у = |
x + 3 + |
|
|
|
является множество |
||||
|
|
|
|
||||||
|
|
|
|
|
|||||
|
6 - x |
||||||||
точек вида
-: A = {x Î(-¥, -3) È[6,¥)} +: B = {x Î[-3,6)}
7

-: C = { x [−3,6]} -: D = { x (−3,6]} I:
S: Областью определения функции у = 
 9 − x2 является множество точек
9 − x2 является множество точек
вида
-: A = { x (∞, −3) [3,∞)} -: B = { x (∞, −3] [3,∞)} -: C = { x (−3,3)}
+ : D = { x [−3,3]} I:
S: Областью определения функции у = 
 x2 − 4x + 3 является множество
x2 − 4x + 3 является множество
точек вида
-: A = { x [3,∞)} -: B = { x (1,∞)}
+ : C = { x (−∞,1] [3,∞} -: D = { x [1,3]}
I:
S: Областью определения функции у = 
 5x − x2 − 6 является множество
5x − x2 − 6 является множество
точек вида
-: A = { x (−∞, 2] [3,∞)} -: B = { x (−∞, 2) (3,∞)}
-: C = { x (2,3)} +: D = { x [2,3]} I:
S: Областью определения функции у = log3 3 2x − 6 является множество
2x − 6 является множество
точек вида
+: A = { x (3,∞)} -: B = { x (−∞,∞)} -: C = { x (−∞,3)} -: D = { x [0,∞)} I:
S: Областью определения функции у = |
|
2 |
|
является множество |
|
|
|
|
|||
x2 − 3x + 2 |
|||||
|
|
|
|
точек вида
+: A = {x (−∞,1) (2,∞)} -: B = {x (−∞,1] [2,∞)}
8
-: C = {x Î(1, 2)} -: D = {x Î[0,¥)} I:
S: Областью определения функции
вида
-: A = {x : x ¹ 1}
-: B = {x Î(-¥,1) È (2,¥)} -: C = {x : x ¹ 2}
+: D = {x : x ¹1, x ¹ 2} I:
S: Областью определения функции
точек вида
-: A = {x Î(-¥,1] È[2,¥)} +: B = {x Î(-¥,1] È (2,¥)}
-: C = {x Î(1, 2)} -: D = {x : x ¹ 2}
I:
S: Областью определения функции
точек вида
-: A = {x Î(-¥,¥)} -: B = {x Î[0,3]} +: C = {x Î(0,3)} -: D = {x Î(-¥,3]}
3 |
|
у = x2 - 3x + 2 |
является множество точек |
у=  x2 - 3x + 2 является множество
x2 - 3x + 2 является множество
x- 2
у= log5 (3x − x2 ) является множество
I:
S: Количество целых чисел, принадлежащих области определения функции
равно …
+: 4
I:
S: Количество целых чисел, принадлежащих области определения функции
равно …
+: 4 I:
9
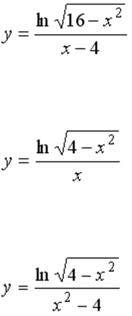
S: Количество целых чисел, принадлежащих области определения функции
равно …
+: 7
I:
S: Количество целых чисел, принадлежащих области определения функции
равно …
+: 2
I:
S: Количество целых чисел, принадлежащих области определения функции
равно …
+: 3
V2: Предел на бесконечности
I:
S: Предел функции
+: 1 I:
S: Предел функции
+: 5 I:
S: Предел функции
+: 5 I:
S: Предел функции
+: 2 I:
S: Предел функции
+: 1/2 I:
S: Предел функции
+: 3
lim |
2x5 + 7x3 − 5 |
равен ... |
|||||||
2x5 − |
4x |
|
|
||||||
x→∞ |
|
|
|
|
|
||||
lim |
10x4 + 7x3 − 5x |
|
равен ... |
||||||
2x4 − 4x + 1 |
|
|
|||||||
x→∞ |
|
|
|
||||||
lim |
30x5 + 8x4 − 5x |
|
равен ... |
||||||
6x5 + 4x |
|
|
|
|
|||||
x→∞ |
|
|
|
|
|
||||
lim |
4x5 + 7x3 − 5 |
равен ... |
|||||||
2x5 − |
4x |
|
|
||||||
x→∞ |
|
|
|
|
|
||||
lim |
3x5 + 8x |
4 − 5х |
равен ... |
||||||
6x5 + 4x |
|
|
|||||||
x→∞ |
|
|
|
|
|
||||
lim |
6x4 + x3 − 5 |
|
равен ... |
||||||
2x4 − x |
|||||||||
x→∞ |
|
|
|
|
|
||||
10
