080100Экономика(МатАнализ и ЛинАлгебра) / Математический анализ_080100_заоч_1_курс_экз_паспорт
.pdf
-: x − sin x cos x 2
x cos x
I:
S: Производная функции y = sin(2x2 − 5) равна…
-: −4x cos(2x2 − 5) -: cos(2x2 − 5)
+: 4x cos(2x2 − 5) -: − cos(2x2 − 5) I:
S: Производная функции y = arctg (1 + 3x2 ) равна…
-:
6x
1 + x2
-:
1
1 + (1 + 3x2 )2
+:
6x
1 + (1 + 3x2 )2
-:
6x
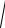1 − (1 + 3x2 )2
I:
S: Производная функции y = ln (x2 + 4) равна…
+:
2x
x2 + 4 -: 2x
x
-:
1
x2 + 4
-: 1 (x2 + 4) + ln 2x x
I:
S: Производная функции y = arcsin (1 − 2x) равна…
-:
1
-:
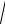1 − x2 −2
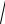1 − x2
+:
−2
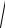1 − (1 − 2x)2
41
-: |
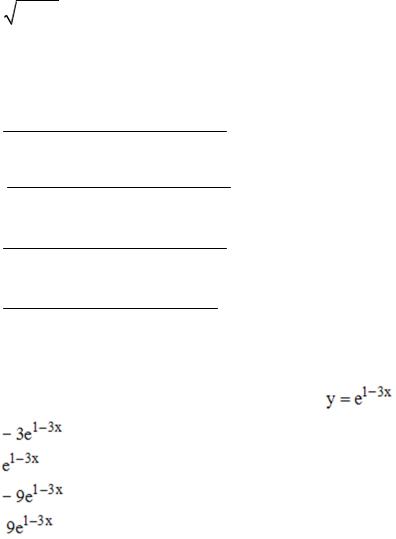
1 |
|
(1 |
− 2x) + arcsin(−2) |
|
|||
|
|
|
|
|||||
|
1 − x2 |
|
|
|
||||
I: |
|
|
|
|
|
1 + ex |
|
|
S: Производная функции y = |
равна… |
|||||||
2x − x3 |
||||||||
|
|
|
|
|
|
|
||
ex (2x − x3 ) − (1 + ex )(2 − 3x2 )
-: (2x − x3 )
+: ex (2x − x3 ) − (1 + ex )(2 − 3x2 )
(2x − x3 )2
-: ex (2x − x3 ) + (1 + ex )(2 − 3x2 )
(2x − x3 )2
-: ex (2x − x3 ) − (1 + ex )(2 − x2 )
(2x − x3 )2
V2: Производные высших порядков
I: |
|
|
|||
S: Производная второго порядка функции |
|
равна … |
|||
-: |
|
|
|
|
|
-: |
|
|
|
|
|
-: |
|
|
|
|
|
+: |
|
|
|
|
|
I: |
|
|
|||
S: Производная второго порядка функции y = |
x6 |
|
− 3x2 + 4x + 2 в точке x = 1 |
||
|
|
||||
6 |
|
0 |
|||
|
|
|
|||
равна ... |
|
|
|||
+: -1 |
|
|
|
|
|
I: |
|
|
|||
S: Производная второго порядка функции y = |
x3 |
|
|
− x2 + x в точке x = 1 равна |
|
|
|||||
3 |
|
0 |
|||
|
|
|
|||
... |
|
|
|
|
|
+: 0 |
|
|
|
|
|
I: |
|
|
|||
S: Производная второго порядка функции y = |
x7 |
|
+ 3x2 − 4x в точке x = 1 |
||
|
|
||||
7 |
|
0 |
|||
|
|
|
|||
равна ... |
|
|
|||
+: 12 |
|
|
|
|
|
I: |
|
|
|||
42
S: Производная второго порядка функции y = x4 + x3 − 7 в точке x = 1 равна |
|||||||
|
|
|
0 |
|
|
|
|
... |
|
|
|
|
|
|
|
+: 18 |
|
|
|
|
|
|
|
I: |
|
|
|
|
|
||
S: Производная второго порядка функции y = x3 − 3x2 − 9x в точке x |
|
= 1 |
|||||
|
|
|
0 |
|
|
|
|
равна ... |
|
|
|
|
|
||
+: 0 |
|
|
|
|
|
|
|
I: |
|
|
|
|
|
||
S: Производная второго порядка функции y = |
|
x8 |
|
+ 2x5 − 7х в точке x |
|
|
= 1 |
|
|
|
|
||||
8 |
0 |
|
|
||||
|
|
|
|
|
|||
равна ... |
|
|
|
|
|
||
+: 47 |
|
|
|
|
|
|
|
I: |
|
|
|
|
|
||
S: Производная второго порядка функции y = 2x |
4 − x3 − 2х2 в точке x |
|
|
= 1 |
|||
|
|
|
0 |
|
|||
равна ... |
|
|
|
|
|
||
+: 14 |
|
|
|
|
|
|
|
I: |
|
|
|
|
|
||
S: Производная второго порядка функции y = x10 − 2x3 − 7 в точке x |
= 1 |
||||||
|
|
|
0 |
|
|
|
|
равна ... |
|
|
|
|
|
||
+: 78 |
|
|
|
|
|
|
|
I: |
|
|
|
|
|
||
S: Производная второго порядка функции y = |
x4 |
|
+ 2x3 − 7х в точке x |
|
|
= 1 |
|
|
|
|
|
||||
4 |
0 |
|
|
||||
|
|
|
|
|
|||
равна ... |
|
|
|
|
|
||
+: 15 |
|
|
|
|
|
|
|
I: |
|
|
|
|
|
||
S: Производная второго порядка функции y = x15 − 2x3 − 7 в точке x |
= 1 |
||||||
0
равна ...
+: 198
V2: Приложения дифференциального исчисления ФОП.
I:
S: Функция y = 2x4
4
-: 0
+: 4 -: Ни при каком х
-: 2 I:
S: Функция y = 4x3
3
-: 0
−8х3 − 2 имеет минимум при x = ...
3
+36х − 7 имеет минимум при x = ...
43
-: 4
-: 2 +: Ни при каком х
I:
S: Функция y = x3
3
+: 1
-: 5 -: Ни при каком х
-: 3 I:
S: Функция y = x 4
2
-: Ни при каком х
-: -4 +: 0 -: 4 I:
S: Функция y = x3
3
+: Ни при каком х
-: -2 -: 4 -: 0
I:
S: Функция y = х3
3
-: 1
+: 5 -: Ни при каком х
-: 3 I:
S: Функция y = x 4
2
-: Ни при каком х
-: -4 +: 0 -: 4 I:
−3х2 + 5х имеет максимум при x =
−16х2 + 5 имеет максимум при x =
−х2 + 8х имеет минимум при x = ...
−3х2 + 5x имеет минимум при x = ...
+ 16х2 − 5 имеет минимум при x = .........
44
S: Функция y = 4x3 − 36х − 7 имеет максимум при x = ...
3
-: Ни при каком х
+: -3 -: 3 -: 1 I:
S: График функции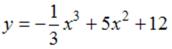 
обращен выпуклостью вверх на промежутке …
+: 
-: 
-: 
-: 
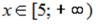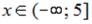
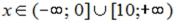
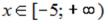I:
S: Функция y = x5 − 2x2 + 4x + 2 является вогнутой на интервале
5
-: A = {x (−∞,∞)}
+: B = {x (1,∞)} -: C = {x (−∞,1)}
I:
S: Функция y = x3 − x2 + x является вогнутой на интервале
3
-: A = {x (−∞,∞)}
+: B = {x (1,∞)} -: C = {x (−∞,1)} I:
S: Функция y = x7 + 3x2 − 4x является вогнутой на интервале
7
-: A = {x (−∞,∞)} +: B = {x (−1,∞)} -: C = {x (−∞, −1)}
I:
S: Функция y = x4 + x3 − 7 является вогнутой на интервале
|
|
|
1 |
|
|
+: A = x |
−∞, − |
|
|
(0,∞) |
|
|
|||||
|
|
|
2 |
|
|
45
|
|
|
1 |
|
-: B = x |
−∞, − |
|
|
|
|
||||
|
|
|
2 |
|
-: C = {x (0, ∞)} |
|
|
||
I:
S: Функция y = x3 − 3x2 − 9x является вогнутой на интервале
-: A = {x (−∞,∞)}
+: B = {x (1,∞)} -: C = {x (−∞,1)}
I:
S: Функция y = x4 − x3 − 7 является вогнутой на интервале
4
+: A = {x (−∞, 0) (2, ∞)} -: B = {x (2, ∞)}
-: C = {x (0, 2)} I:
S: Функция y = x5 + 2x3 − 7х является вогнутой на интервале
5
-: A = {x (−∞,0) (3,∞)}
+: B = {x (0,∞)} -: C = {x (−∞,0)}
I:
S: Функция y = 2x3 − 2x2 − 7 является вогнутой на интервале
3
-: A = {x (−∞,∞)}
+: B = {x (1,∞)} -: C = {x (−∞,1)}
I:
S: Функция, график которой представлен на рисунке,
имеет … точек перегиба.
46
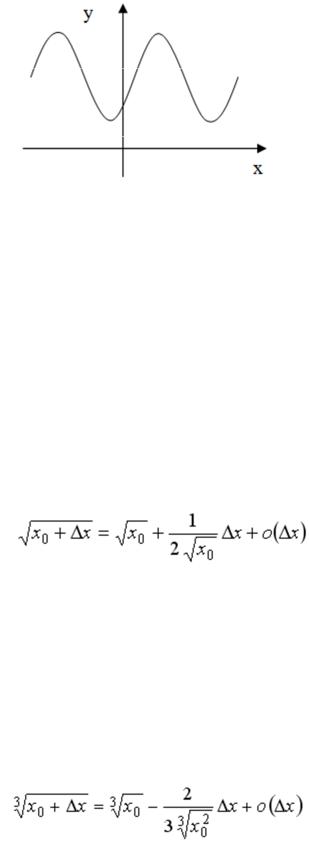
+: 2
I:
S: Функция, график которой представлен на рисунке,
имеет … точек перегиба. +: 3
I:
S: Значение функции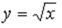 
в точке 
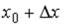можно вычислить по формуле
…
-: 
-: 
-: 
+:
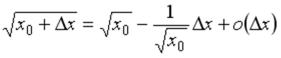
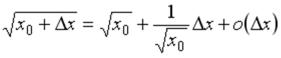
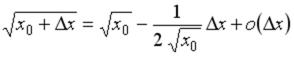
I:
S: Значение функции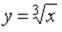 
в точке 
можно вычислить по формуле
…
-: 
-: 
-:
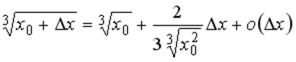
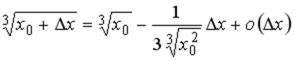
47
+:
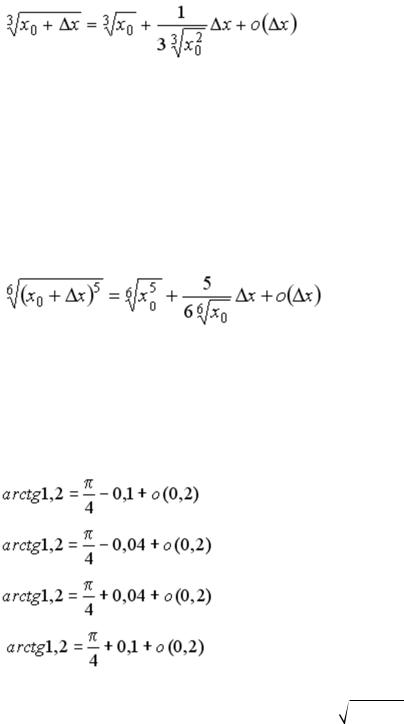
I:
S: Значение функции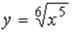 
в точке 
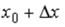можно вычислить по формуле
…
-: 
-: 
+:
-: 
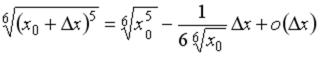
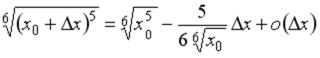
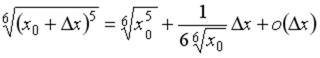I:
S: Значение функции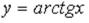 
в точке 
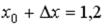можно вычислить по формуле …
-:
-:
-:
+:
I:
S: Приближенное значение функции f (x) = 
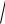x2 + 3x при
x = 0.94 вычисленное с использованием дифференциала первого порядка, равно …
-: 1.925 -: 2.075 -: 1.25 +: 1.85 I:
48
S: Дифференциал функции y = sin 5x + cos p имеет вид …
3
|
π |
-: 5cos5x − sin |
dx |
|
3 |
-: 5cos 5x
+: 5cos5x × dx
-: cos5x × dx
V1: Дифференциальное исчисление функций нескольких переменных
V2: Частные производные первого порядка.
I:
S: Частная производная функции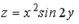 
по переменной y в точке 
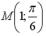равна…
-: –1 -: 2 +: 1 -: 0
I:
S: Частная производная функции z = x3 cos 4 y по переменной y в точке
M 1, π равна…
2
-: – 1 -: 4 -: -4 +: 0
I:
S: Частная производная функции z = x3 cos 2 y по переменной x в точке
M 1, π равна…
2
-: – 1 -: 3 -: -3 +: 0
I:
S: Частная производная функции z = x3tgy по переменной y в точке M (1,0) равна…
-: – 1 -: 0,5 +: 1
49
-: 0 |
|
|
|
|
I: |
|
|
|
π |
S: Частная производная функции |
3 |
по переменной x |
||
z = x tgy |
в точке M 1, |
|
||
|
|
|
|
4 |
равна…
-: – 0,5 -: 0,5 +: 3 -: 0
I:
S: Частная производная функции z = (x3 + x)tgy по переменной x в точке
M 1, π равна…
4
-: – 0,5 -: 0,5 +: 4 -: -4 I:
S: Частная производная функции z = (x3 + x)tgy по переменной y в точке M (1,0) равна…
-: – 0,5 -: 0,5 +: 2 -: -2 I:
S: Частная производная функции z = (2x2 + 3x) ln y по переменной y в точке M (1,1) равна…
-: – 2 -: 0,5 +: 5 -: 0
I:
S: Частная производная функции z = (2x2 + 3x) ln y по переменной x в точке M (1,1) равна…
-: – 2 -: 0,5 +: 0 -: 7 I:
50