080100Экономика(МатАнализ и ЛинАлгебра) / Математический анализ_080100_заоч_1_курс_экз_паспорт
.pdf
S: Частная производная функции z = x4 ln 4 y по переменной x в точке
|
1 |
|
|
|
M 1, |
|
|
равна… |
|
4 |
||||
|
|
|
-: – 8 -: 0,5 +: 0 -: 4 I:
S: Частная производная функции z = 6x4 ln 4 y по переменной y в точке M (1,1) равна…
-: –2 -: 4 +: 6 -: 1
I:
S: Частная производная функции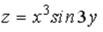 
по переменной y в точке
равна…
-: 3 +: 1,5 -: 1 -: 0,5
I:
S: Частная производная функции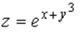 
по переменной y в точке
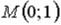равна…
-: е -: 2е +: 3е -: 3
I:
S: Частная производная функции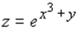 
по переменной x в точке 
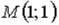равна…
+: 
-: 
-: 
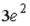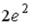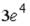
51
-: 
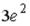
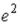I:
S: Частная производная функции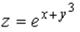 
по переменной y в точке 
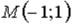равна…
-: – 3 |
|
|
|||||||
-: |
|
|
|
|
|
|
|
|
|
-: 1 |
|
|
|
|
|
|
|
||
+: 3 |
|
|
|
|
|
|
|||
I: |
|
|
|
|
|
|
|
||
S: Частная производная z′ |
функции z = x3 + 5xy − 3y3 + 2x − y − 1 равна … |
||||||||
|
|
|
|
|
|
|
|
y |
|
-: 3x2 + 5 y + 2 |
|
|
|||||||
-: 5 y − 9 y2 −1 |
|
|
|||||||
-: 3x2 + 5x + 5 y − 9 y2 + 1 |
|
|
|||||||
+: 5x − 9 y2 − 1 |
|
|
|||||||
I: |
|
|
|
|
|
|
|
||
S: Частная производная z′ |
функции z = x3 + 5xy − 3y3 + 2x − y − 1 равна … |
||||||||
+: 3x2 + 5 y + 2 |
x |
|
|||||||
|
|
||||||||
-: 5 y − 9 y2 −1 |
|
|
|||||||
-: 3x2 + 5x + 5 y − 9 y2 + 1 |
|
|
|||||||
-: 5x − 9 y2 − 1 |
|
|
|||||||
I: |
|
|
|
|
|
∂z |
|
||
S: Частная производная |
функции z = arctg(2x − 3y) равна … |
||||||||
|
|
|
|
|
|
|
|
∂x |
|
-: |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ (2x − 3y)2 |
|
|
|||||
1 |
|
|
|||||||
+: |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + (2x − 3y)2 |
|
|
|||||||
|
|
|
|||||||
-: |
|
|
|
2 − 3y |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
+ (2x − 3y)2 |
|
|
|||||
1 |
|
|
|||||||
-: − |
3 |
|
|
|
|
|
|||
|
|
|
|
|
|||||
1 + (2x − 3y)2 |
|
|
|||||||
I: |
|
|
|
|
|
∂z |
|
||
S: Частная производная |
функции z = arctg(2x − 3y) равна … |
||||||||
|
|
|
|
|
|
|
|
∂y |
|
-: |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ (2x − 3y)2 |
|
|
|||||
1 |
|
|
|||||||
52
-: |
|
|
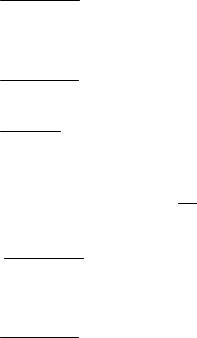
2 |
|
|
+ (2x − 3y)2 |
|||
1 |
||||
-: |
|
|
2 − 3y |
|
|
+ (2x − 3y)2 |
|||
1 |
||||
+: − |
3 |
|
||
|
||||
1 + (2x − 3y)2 |
||||
I: |
|
|
|
|
S: Частная производная z′
x
-: 3x2 cos 4 y - x3 × 4sin 4 y -: 3x2 cos 4 y - x3 sin 4 y
-: -x3 × 4sin 4 y +: 3x2 cos 4 y I:
S: Частная производная z′y
-: 3x2 cos 4 y - x3 × 4sin 4 y -: 3x2 cos 4 y - x3 sin 4 y +: -x3 × 4sin 4 y
-: 3x2 cos 4 y I:
S: Частная производная ∂z
¶x
-: (2x2 + 3x) y
+: (4x + 3)ln y
-: (2x2 + 3x) + (4x + 3) ln y y
-: (4x + 3) y
I:
S: Частная производная ∂z
∂y
+: (2x2 + 3x) y
-: (4x + 3)ln y
-: (2x2 + 3x) + (4x + 3) ln y y
функции z = x3 cos 4 y равна …
функции z = x3 cos 4 y равна …
функции z = (2x2 + 3x) ln y равна …
функции z = (2x2 + 3x) ln y равна …
53
-: (4x + 3) y
V2: Частные производные высших порядков
I:
S: Частная производная второго порядка по переменной y функции
z = 3x2 − xy2 + 2 y3 − xy + 2 в точке M |
0 |
(5;1) равна … |
|
|
|
-: 6 |
|
|
-: –3 |
|
|
+: 2 |
|
|
-: 4 |
|
|
I: |
|
|
S: Частная производная второго порядка по переменной x функции
z = 3x2 − xy2 + 2 y3 − xy + 2 в точке M |
0 |
(5;1) равна … |
|
|
|
+: 6 |
|
|
-: –3 |
|
|
-: 2 |
|
|
-: 4 |
|
|
I:
S: Смешанная производная второго порядка функции
z = 3x2 − xy2 + 2 y3 − xy + 2 в точке M |
0 |
(5;1) равна … |
|
|
|
-: 6 |
|
|
+: –3 |
|
|
-: 2 |
|
|
-: 4 |
|
|
I: |
|
|
S: Частная производная второго порядка по переменной y функции
z = 3x2 − x2 y2 + 2 y3 − xy + 2 в точке M |
0 |
(−1;1) равна … |
|
|
|
-: 4 |
|
|
-: 3 |
|
|
-: 2 |
|
|
+: 10 |
|
|
I: |
|
|
S: Частная производная второго порядка по переменной x функции
z = 3x2 − x2 y2 + 2 y3 − xy + 2 в точке M |
0 |
(−1;1) равна … |
|
|
|
+: 4 |
|
|
-: 3 |
|
|
-: 2 |
|
|
-: 10 |
|
|
I: |
|
|
S: Смешанная производная второго порядка функции |
||
z = 3x2 − x2 y2 + 2 y3 − xy + 2 в точке M |
0 |
(−1;1) равна … |
|
|
|
-: 6 |
|
|
54
+: 3 -: 2 -: 10
I:
S: Частная производная второго порядка по переменной y функции
z = 3x2 − x2 y + 2 y3 − xy + 2 в точке M |
0 |
(−1;1) равна … |
|
|
|
-: 6 |
|
|
+: –12 |
|
|
-: -3 |
|
|
-: 8 |
|
|
I: |
|
|
S: Частная производная второго порядка по переменной x функции |
||
z = 3x2 − x2 y + 2 y3 − xy + 2 в точке M |
0 |
(−1;1) равна … |
|
|
|
-: 6 |
|
|
-: –12 |
|
|
-: -3 |
|
|
+: 8 |
|
|
I: |
|
|
S: Смешанная производная второго порядка функции |
||
z = 3x2 − x2 y + 2 y3 − xy + 2 в точке M |
0 |
(−1;1) равна … |
|
|
|
-: 6 |
|
|
-: –12 |
|
|
+: -3 |
|
|
-: 8 |
|
|
I: |
|
|
S: Смешанная производная второго порядка функции z = ln(2x − 3y) равна …
+:
6
(2x − 3y)2
-:
1
(2x − 3y)2
-: − |
9 |
|
(2x − 3y)2 |
||
|
-: − |
4 |
|
(2x − 3y)2 |
||
|
I:
S: Частная производная второго порядка по переменной x функции z = ln(2x − 3y) равна …
-:
6
(2x − 3y)2
-:
1
(2x − 3y)2
55
-: − |
|
9 |
|
|
(2x − 3y)2 |
||||
|
||||
+: − |
4 |
|
||
|
|
|||
(2x − 3y)2 |
||||
|
|
|||
I:
S: Частная производная второго порядка по переменной y функции z = ln(2x − 3y) равна …
-:
6
(2x − 3y)2
-:
1
(2x − 3y)2
+: − |
9 |
|
||
(2x − 3y)2 |
||||
|
|
|||
-: − |
|
4 |
|
|
|
|
|
||
(2x − 3y)2 |
||||
|
||||
I:
S: Смешанная производная второго порядка функции z = cos(2x − 3y) равна …
+: z = 6cos(2x − 3y) -: z = −9cos(2x − 3y) -: z = −4cos(2x − 3y) -: z = − cos(2x − 3y)
I:
S: Частная производная второго порядка по переменной y функции z = cos(2x − 3y) равна …
-: z = 6cos(2x − 3y) +: z = −9cos(2x − 3y) -: z = −4cos(2x − 3y) -: z = − cos(2x − 3y)
I:
S: Частная производная второго порядка по переменной x функции z = cos(2x − 3y) равна …
-: z = 6cos(2x − 3y) -: z = −9cos(2x − 3y) +: z = −4cos(2x − 3y) -: z = − cos(2x − 3y) I:
56
S: Смешанная производная второго порядка функции z = sin(2x − 3y) равна …
+: z = 6sin(2x − 3y) -: z = −9sin(2x − 3y) -: z = −4sin(2x − 3y) -: z = −sin(2x − 3y)
I:
S: Частная производная второго порядка по переменной y функции z = sin(2x − 3y) равна …
-: z = 6sin(2x − 3y) +: z = −9sin(2x − 3y) -: z = −4sin(2x − 3y) -: z = −sin(2x − 3y)
I:
S: Частная производная второго порядка по переменной x функции z = sin(2x − 3y) равна …
-: z = 6sin(2x − 3y) -: z = −9sin(2x − 3y) +: z = −4sin(2x − 3y) -: z = −sin(2x − 3y)
V2: Полный дифференциал, производная по направлению, градиент.
I:
S: Выражение (3x2 + 2)dx + (2 y + 2)dy является полным дифференциалом функции …
-: z = x3 + y2 + 2 -: z = 3x2 + 2 y + 4
-: z = x3 + 2xy + y2 −1
+: z = x3 + 2x + y2 + 2 y − 3 I:
S: Выражение (3x2 + 2 y) cos(x3 + 2xy)dx + 2 yx cos(x3 + 2xy)dy является полным дифференциалом функции …
-: z = cos(x3 + 2xy) -: z = − sin(x3 + 2xy) -: z = − cos(x3 + 2xy) +: z = sin(x3 + 2xy) I:
57
S: Полный дифференциал функции z = ln(x2 − xy − y2 ) равен …
+: dz = |
2x − y |
|
dx − |
x + 2 y |
|
dy |
||||||
x2 − xy − y2 |
|
x2 − xy − y2 |
|
|||||||||
1 |
|
1 |
|
|
|
|
||||||
-: dz = |
|
|
dx + |
|
|
|
dy |
|||||
x2 − xy − y2 |
x2 − xy − y2 |
|||||||||||
-: dz = |
|
2x −1 |
dx − |
|
|
2 y + 1 |
dy |
|||||
|
|
|
|
|||||||||
x2 − xy − y2 |
x2 − xy − y2 |
|||||||||||
-: dz = |
|
x + 2 y |
dx + |
|
2x − y |
dy |
||||||
|
|
|
|
|||||||||
x2 − xy − y2 |
x2 − xy − y2 |
|||||||||||
I: |
|
|
|
|
|
|
|
|
|
|||
S: Полный дифференциал функции z = x2 + 5xy + 3y2 равен … |
||||||||||||
-: dz = (2x + 5)dx + (5 + 6 y)dy |
|
|
||||||||||
-: dz = (x2 + 5xy + 3y2 )dxdy
+: dz = (2x + 5 y)dx + (5x + 6 y)dy -: dz = (5x + 6 y)dx + (2x + 5 y)dy I:
S: Полный дифференциал функции z = x2 − 10xy + 2 y2 равен …
-: dz = (2x − 10)dx + (−10 + 2 y)dy
-: dz = (x2 − 10xy + 2 y2 )dxdy
+: dz = (2x − 10 y)dx + (−10x + 4 y)dy -: dz = (5x + 6 y)dx + (2x + 5 y)dy
I:
S: Полный дифференциал функции z = 2x2 − 3xy + y3 в точке
M 0 (2;1) равен … +: 5dx − 3dy
-: 5dx
-: −3dx + 5dy -: −2dx + 9dy I:
S: Полный дифференциал функции z = 4x2 + 3xy + y3 в точке
M 0 (2;1) равен … +: 19dx + 9dy
-: 28dx
-: 9dx + 19dy -: −2dx + 9dy I:
58
S: Полный дифференциал функции z = 4x2 − 3x2 y + y3 в точке
+: 4dx − 9dy |
|
|
|
|
|
-: −5dx |
|
|
|
|
|
-: −9dx + 4dy |
|
|
|
|
|
-: −2dx + 9dy |
|
|
|
|
|
I: |
|
|
|
|
|
S: Градиент функции z = 2x2 − 3xy + y3 |
в точке M |
0 |
(2;1) равен … |
||
|
− 3 j |
|
|
|
|
+: 5i |
|
|
|
|
|
-: 5i |
|
|
|
|
|
-: −3i |
+ 5 j |
|
|
|
|
-: −2i |
+ 9 j |
|
|
|
|
I: |
|
|
|
|
|
S: Градиент функции z = 4x2 + 3xy + y3 |
в точке M |
0 |
(2;1) равен … |
||
+: 19i + 9 j |
|
|
|
||
|
|
|
|
||
-: 28i |
|
|
|
|
|
-: 9i + 19 j |
|
|
|
|
|
-: −2i |
+ 9 j |
|
|
|
|
I: |
|
|
|
|
|
S: Градиент функции z = 4x2 − 3x2 y + y3 в точке M |
0 |
(2;1) равен … |
|||
|
− 9 j |
|
|
|
|
+: 4i |
|
|
|
|
|
-: −5i |
|
|
|
|
|
-: −9i |
+ 4 j |
|
|
|
|
-: −2i |
+ 9 j |
|
|
|
|
I: |
|
|
|
|
|
S: Градиент функции z = 4x3 − 3x2 y + y3 в точке M |
0 |
(1;1) равен … |
|||
-: 6i − 3 j |
|
|
|
||
|
|
|
|
||
+: 6i |
|
|
|
|
|
-: −6i |
− 5 j |
|
|
|
|
-: −4i |
|
|
|
|
|
I: |
|
|
|
|
(1;1) равен … |
S: Градиент функции z = 4x3 − 3x2 y + y2 в точке M |
|
||||
M 0 (2;1) равен … |
|
|
|
|
|
0
+: 6i − j
-: 6i
-: −6i − j
-: 6i + j I:
59
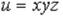
S: Производная функции z = 2x2 − 3xy + y3 |
по направлению вектора |
|
|
|
|
|
|
ℓ0 (cos α;cosβ) в точке M 0 (2;1) |
имеет вид … |
|
|
+: 5cos α − 3cosβ |
|
|
|
-: 5cos α + 4cosβ |
|
|
|
-: −3cos α + 5cosβ |
|
|
|
-: −2cos α + 9cosβ |
|
|
|
I: |
|
|
|
S: Производная функции z = 4x2 + 3xy + y3 |
по направлению вектора |
|
|
|
|
|
|
ℓ0 (cos α;cosβ) в точке M 0 (2;1) |
имеет вид … |
|
|
+: 19cos α + 9cosβ |
|
|
|
-: 28cos α |
|
|
|
-: 9cos α + 19cosβ |
|
|
|
-: −2cos α + 9cosβ |
|
|
|
I: |
|
|
|
S: Производная функции z = 4x2 − 3x2 y + y3 по направлению вектора |
|
||
|
|
|
|
ℓ0 (cos α;cosβ) в точке M 0 (2;1) |
имеет вид … |
|
|
+: 4cos α − 9cosβ |
|
|
|
-: −5cos α |
|
|
|
-: −9cos α + 4cosβ |
|
|
|
-: −2cos α + 9cosβ |
|
|
|
I: |
|
|
|
S: Производная функции z = 4x3 − 3x2 y + y3 по направлению вектора |
|
||
|
|
|
|
ℓ0 (cos α;cosβ) в точке M 0 (1;1) |
имеет вид … |
|
|
-: 6cos α − 3cosβ |
|
|
|
+: 6cos α |
|
|
|
-: −6cos α − 5cosβ |
|
|
|
-: −4 cos α |
|
|
|
I: |
|
|
|
S: Производная функции z = 4x3 − 3x2 y + y2 по направлению вектора |
|
||
|
|
|
|
ℓ0 (cos α;cosβ) в точке M 0 (1;1) |
имеет вид … |
|
|
+: 6cos α − cosβ |
|
|
|
-: 6cos α |
|
|
|
-: −6cosα − cosβ |
|
|
|
-: −6cos α + cosβ |
|
|
|
I: |
|
|
|
S: Направление наискорейшего возрастания скалярного поля |
в точке |
||
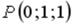совпадает с направлением вектора …
-: 
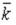
60