
- •Информатика Учебное пособие
- •Содержание
- •Предисловие
- •Тема 1. Введение
- •1.1. Цель и задачи курса «Информатика»
- •1.2. Объекты и составные части информатики
- •1.3. Информатика как единство науки и технологии
- •Контрольные вопросы
- •Тема 2. Основные понятия информатики
- •2.1. Место информатики в системе наук
- •2.2. Основные понятия курса «Информатика»
- •Предмет информатики составляют следующие понятия:
- •Информация классифицируется по видам. (рис. 2.4.)
- •Тема 3. Основы дискретной математики.
- •3.2. Основы логики
- •Элементарные булевые функции
- •Из них выделим функцию "отрицание X" (обозначается -X). Эта функция представлена в таблице
- •3.3. Графы и деревья
- •А) граф g; б) остов графа g; в) другой остов графа g
- •Тема 4. Основные понятия архитектуры эвм
- •Для представления числовых данных в эвм используются естественная и нормальная формы записи чисел.
- •4.2. Системы счисления. Правила перевода чисел из одной системы счисления в другую
- •3. Арифметические операции
- •4.3. Логические элементы компьютера
- •В качестве важных последовательностных схем, выполняемых на одной ис, можно отметить счетчики, сдвиговые регистры, элементы памяти и др.
- •Структурная схема базовой модели мп фирмы Intel представлена на рисунке 4.15.
- •4.5. Организация памяти компьютера
- •Используется два основных типа оперативной памяти:
- •Контрольные вопросы
- •Тема 5. Алгоритмическое решение задач, анализ алгоритмической сложности.
- •5.1. Стратегия решения задач.
- •5.2. Алгоритмы (свойства, реализация алгоритмов)
- •5.3. Структуры данных
- •5.4. Основные вычислительные алгоритмы.
- •5.5. Анализ алгоритмов
- •1. Сравнительные оценки алгоритмов
- •2. Система обозначений в анализе алгоритмов
- •3. Классификация алгоритмов по виду функции трудоёмкости
- •4. Асимптотический анализ алгоритмов
- •Контрольные вопросы
- •Тема 6. Знакомство с языками программирования.
- •6.1. Обзор языков программирования
- •6.2. Основные конструкции программирования
- •Внутри программы значение свойств можно изменять как угодно часто.
- •Константы.
- •На практике наибольшее распространение получили язык функционального программирования lisp и два его диалекта: язык Common lisp и язык Scheme.
- •Наиболее распространенным языком логического программирования является язык Prolog (Пролог).
- •Контрольные вопросы
- •Тема 7. Основы операционных систем
- •7.1. Основные концепции операционных систем
- •7.4. Файловые системы
- •7.6. Обзор современного прикладного программного обеспечения
- •Контрольные вопросы
- •Тема 8. Сети и телекоммуникации
- •Компоненты сети
- •По программной совместимости эвм: однородные (гомогенные) и неоднородные (гетерогенные);
- •8.3. Системы телекоммуникаций
- •Типы телекоммуникационных систем
- •Системы телевещания
- •Системы подвижной связи
- •Сети сотовой подвижной связи
- •Сети транкинговой связи
- •Сети персонального радиовызова
- •Сети мобильной спутниковой связи
- •Волоконно-оптические сети
- •Контрольные вопросы:
- •Тема 9. Сеть Internet
- •9.1. Теоретические основы Internet
- •9.2. Основные понятия (сайт, сокет, сервер, клиент). Web как пример архитектуры «клиент-сервер»
- •9.3. Службы Internet
- •Контрольные вопросы:
- •Тема 10. Графическое программное обеспечение
- •10.1. Иерархия графического программного обеспечения. Графические коммуникации. Графические системы.
- •10.2. Системы растровой и векторной графики
- •Описание объекта является простым и занимает мало памяти;
- •10.3. Графические редакторы
- •Контрольные вопросы
- •Тема 11. Основы защиты информации
- •11.1. Информационная безопасность и ее составляющие
- •11.2. Угрозы безопасности информации и их классификация
- •11.3. Сетевая безопасность
- •11.4. Антивирусные программы
- •Контрольные вопросы
4. Асимптотический анализ алгоритмов
Одним из упрощенных видов анализа, используемых на практике, является асимптотический анализ алгоритмов. Целью асимптотического анализа является сравнение затрат времени и других ресурсов различными алгоритмами, предназначенными для решения одной и той же задачи, при больших объемах входных данных.
При анализе поведения функции трудоемкости алгоритма часто используют принятые в математике асимптотические обозначения, позволяющие показать скорость роста функции, маскируя при этом конкретные коэффициенты.
Такая оценка функции трудоемкости алгоритма называется сложностью алгоритма и позволяет определить предпочтения в использовании того или иного алгоритма для больших значений размерности исходных данных.
В асимптотическом анализе приняты следующие обозначения:
1.Оценка Θ(тетта)
Пусть f(n) и g(n) — положительные функции положительного аргумента, n >= 1 (количество объектов на входе и количество операций -положительные числа), тогда:
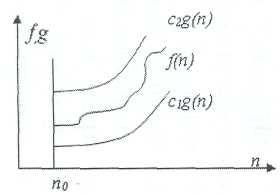
f(n) =Θ(g(n)), если существуют положительные c1, с2, n0, такие, что: cl ·g(n) =< f(n) =< c2 * g(n), при n > n0
Обычно говорят, что при этом функция g(n) является асимптотически точной оценкой функции f(n), т.к. по определению функция f(n) не отличается от функции g(n) с точностью до постоянного множителя.
Отметим, что из f(n) = Θ(g(n)) следует, что g(n) = Θ(f(n)). Примеры:
1) f(n)=4n2+nlnN+174 - f(n)= Θ(n2);
2) f(n)=Θ(l) - запись означает, что f(n) или равна константе, не равной нулю, или f(n) ограничена константой на : f(n) = 7+1/n = Θ(1).
2. Оценка О (О большое)
В отличие от оценки Θ, оценка О требует только, что бы функция f(n) не превышала g(n) начиная с n > n0, с точностью до постоянного множителя:

Вообще, запись O(g(n)) обозначает класс функций, таких, что все они растут не быстрее, чем функция g(n) с точностью до постоянного множителя, поэтому иногда говорят, что g(n) мажорирует функцию f(n).
Например, для всех функций:
f(n)=l/n, f(n)= 12, f(n)=3·n+17, f(n)=n·Ln(n), f(n)=6·n2+24·п+77 будет справедлива оценка О(n2)
Указывая оценку О, есть смысл указывать наиболее «близкую» мажорирующую функцию, поскольку например для f(n)= n2 справедлива оценка О(n2), однако она не имеет практического смысла.
3. Оценка Ω (Омега)
В отличие от оценки О, оценка Ω является оценкой снизу, т.е. определяет класс функций, которые растут не медленнее, чем g(n) с точностью до постоянного множителя:
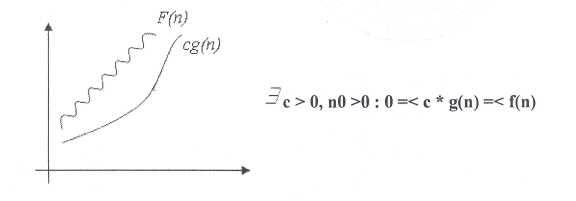
Например, запись Ω (n·Ln(n)) обозначает класс функций, которые растут не медленнее, чем g(n) = n·Ln(n), в этот класс попадают все полиномы со степенью большей единицы, равно как и все степенные функции с основанием большим единицы.
Асимптотическое обозначение О восходит к учебнику Бахмана по теории простых чисел (Bachman, 1892), обозначения Θ,Ω введены Д. Кнутом (Donald Knuth).
Отметим, что не всегда для пары функций справедливо одно из асимптотических соотношений, например для f(n)=n1+sin(n) и g(n)=n не выполняется ни одно из асимптотических соотношений.
В асимптотическом анализе алгоритмов разработаны специальные методы получения асимптотических оценок, особенно для класса рекурсивных алгоритмов. Очевидно, что Θ оценка является более предпочтительной, чем оценка О. Знание асимптотики поведения функции трудоемкости алгоритма - его сложности, дает возможность делать прогнозы по выбору более рационального с точки зрения трудоемкости алгоритма для больших размерностей исходных данных.
В частности, проблема останова также является частично разрешимой проблемой, а проблемы эквивалентности и тотальности не являются таковыми.
