
- •Информатика Учебное пособие
- •Содержание
- •Предисловие
- •Тема 1. Введение
- •1.1. Цель и задачи курса «Информатика»
- •1.2. Объекты и составные части информатики
- •1.3. Информатика как единство науки и технологии
- •Контрольные вопросы
- •Тема 2. Основные понятия информатики
- •2.1. Место информатики в системе наук
- •2.2. Основные понятия курса «Информатика»
- •Предмет информатики составляют следующие понятия:
- •Информация классифицируется по видам. (рис. 2.4.)
- •Тема 3. Основы дискретной математики.
- •3.2. Основы логики
- •Элементарные булевые функции
- •Из них выделим функцию "отрицание X" (обозначается -X). Эта функция представлена в таблице
- •3.3. Графы и деревья
- •А) граф g; б) остов графа g; в) другой остов графа g
- •Тема 4. Основные понятия архитектуры эвм
- •Для представления числовых данных в эвм используются естественная и нормальная формы записи чисел.
- •4.2. Системы счисления. Правила перевода чисел из одной системы счисления в другую
- •3. Арифметические операции
- •4.3. Логические элементы компьютера
- •В качестве важных последовательностных схем, выполняемых на одной ис, можно отметить счетчики, сдвиговые регистры, элементы памяти и др.
- •Структурная схема базовой модели мп фирмы Intel представлена на рисунке 4.15.
- •4.5. Организация памяти компьютера
- •Используется два основных типа оперативной памяти:
- •Контрольные вопросы
- •Тема 5. Алгоритмическое решение задач, анализ алгоритмической сложности.
- •5.1. Стратегия решения задач.
- •5.2. Алгоритмы (свойства, реализация алгоритмов)
- •5.3. Структуры данных
- •5.4. Основные вычислительные алгоритмы.
- •5.5. Анализ алгоритмов
- •1. Сравнительные оценки алгоритмов
- •2. Система обозначений в анализе алгоритмов
- •3. Классификация алгоритмов по виду функции трудоёмкости
- •4. Асимптотический анализ алгоритмов
- •Контрольные вопросы
- •Тема 6. Знакомство с языками программирования.
- •6.1. Обзор языков программирования
- •6.2. Основные конструкции программирования
- •Внутри программы значение свойств можно изменять как угодно часто.
- •Константы.
- •На практике наибольшее распространение получили язык функционального программирования lisp и два его диалекта: язык Common lisp и язык Scheme.
- •Наиболее распространенным языком логического программирования является язык Prolog (Пролог).
- •Контрольные вопросы
- •Тема 7. Основы операционных систем
- •7.1. Основные концепции операционных систем
- •7.4. Файловые системы
- •7.6. Обзор современного прикладного программного обеспечения
- •Контрольные вопросы
- •Тема 8. Сети и телекоммуникации
- •Компоненты сети
- •По программной совместимости эвм: однородные (гомогенные) и неоднородные (гетерогенные);
- •8.3. Системы телекоммуникаций
- •Типы телекоммуникационных систем
- •Системы телевещания
- •Системы подвижной связи
- •Сети сотовой подвижной связи
- •Сети транкинговой связи
- •Сети персонального радиовызова
- •Сети мобильной спутниковой связи
- •Волоконно-оптические сети
- •Контрольные вопросы:
- •Тема 9. Сеть Internet
- •9.1. Теоретические основы Internet
- •9.2. Основные понятия (сайт, сокет, сервер, клиент). Web как пример архитектуры «клиент-сервер»
- •9.3. Службы Internet
- •Контрольные вопросы:
- •Тема 10. Графическое программное обеспечение
- •10.1. Иерархия графического программного обеспечения. Графические коммуникации. Графические системы.
- •10.2. Системы растровой и векторной графики
- •Описание объекта является простым и занимает мало памяти;
- •10.3. Графические редакторы
- •Контрольные вопросы
- •Тема 11. Основы защиты информации
- •11.1. Информационная безопасность и ее составляющие
- •11.2. Угрозы безопасности информации и их классификация
- •11.3. Сетевая безопасность
- •11.4. Антивирусные программы
- •Контрольные вопросы
3. Арифметические операции
Двоичные таблицы сложения вычитания, умножения и деления;
|
0+0=0 |
0-0=0 |
0·0=0 |
1/1=1 |
|
0+1=1 |
1-0=1 |
1·0=0 |
0/1=0 |
|
1+0=1 |
1-1=0 |
0·1=0 |
1 / 0 — нельзя |
|
1+1=10 |
10-1=1 |
1·1=1 |
|
Восьмеричная система счисления
Таблица умножения
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
2 |
4 |
6 |
10 |
12 |
14 |
16 |
|
3 |
3 |
6 |
11 |
14 |
17 |
22 |
25 |
|
4 |
4 |
10 |
14 |
20 |
24 |
30 |
34 |
|
5 |
5 |
12 |
17 |
24 |
31 |
36 |
43 |
|
6 |
6 |
14 |
22 |
30 |
36 |
44 |
52 |
|
7 |
7 |
16 |
25 |
34 |
43 |
52 |
61 |
Таблица сложения
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
|
2 |
|
4 |
5 |
6 |
7 |
10 |
11 |
|
3 |
|
|
6 |
7 |
10 |
11 |
12 |
|
4 |
|
|
|
10 |
11 |
12 |
13 |
|
5 |
|
|
|
|
12 |
13 |
14 |
|
6 |
|
|
|
|
|
14 |
15 |
|
7 |
|
|
|
|
|
|
16 |
Примеры арифметических операций в двойной и восьмеричной системах счисления.
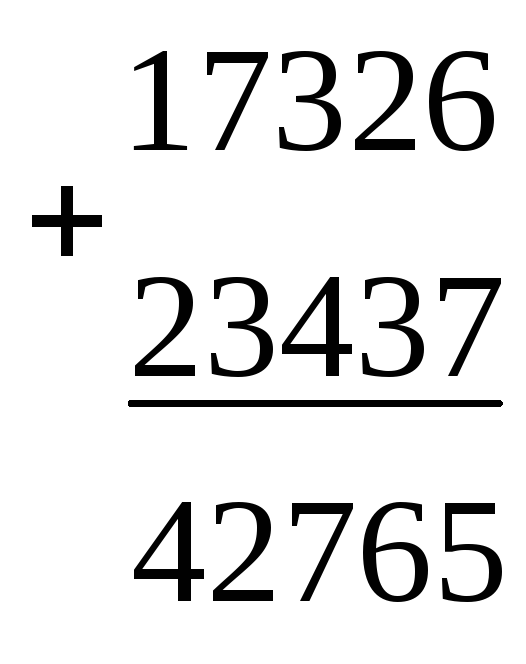

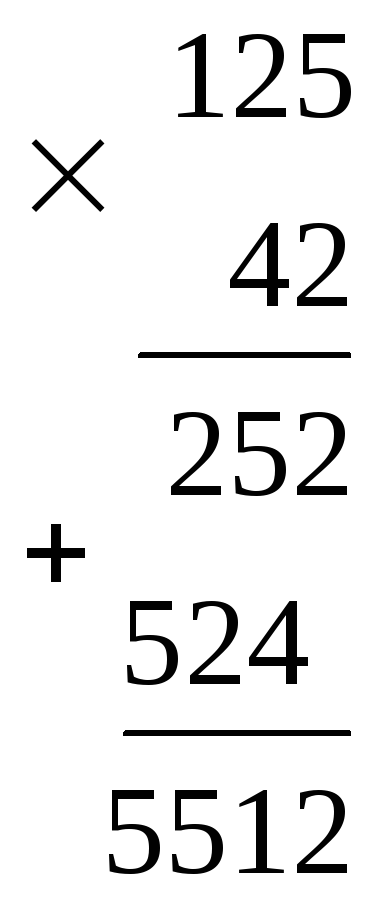
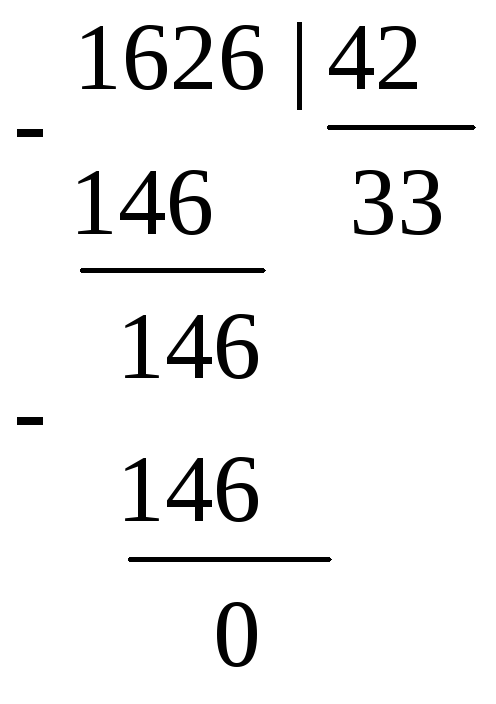


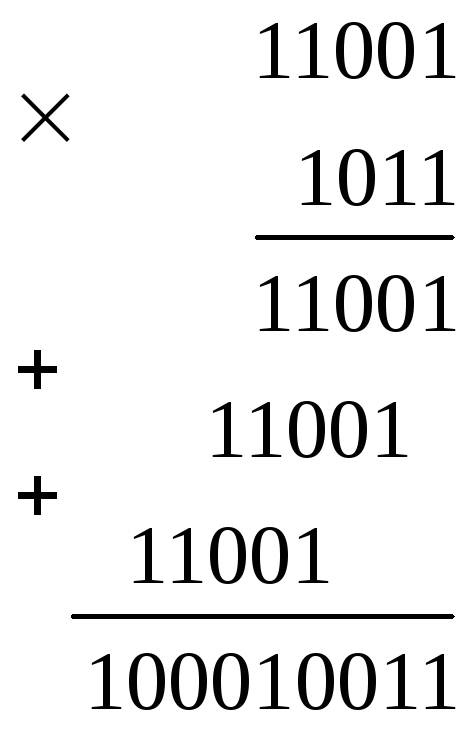

4.3. Логические элементы компьютера
Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и другие (называемые также вентилями), а также триггер. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера.
Для структурно-функционального описания логических схем (ЛС), составляющих основу любого дискретного вычислительного устройства, ЭВМ или ВС в целом, используется аппарат булевой алгебры, созданной в 1854 г. Дж. Булем как попытка изучения логики мышления математическими методами.
Представив ЛС в виде некоторого черного ящика (рис. 4.3.), имеющего п входов и один выход, его поведение можно определять некоторой логической F(x1, x2, ..., хп)-функцией от п логических переменных.
Логическая F-функция может быть задана таблицей истинности (табл. 4.2) или посредством 6улевых выражений; ЛС, представимые одним из этих способов, называются комбинационными.
|
х1 |
|
Логическая схема (ЛС)
|
F(х1, х2 ,…, хn)=YB={0,1} |
|
х2 |
| ||
|
… |
.... | ||
|
… |
.... | ||
|
хn |
|
Рис. 4.3. Формальное представление произвольной логической схемы
Таблица 4.2 Таблица истинности F-функции
|
х1 |
х2 |
.... |
хn-1 |
хn |
F(х1, х2 ,…, хn) |
|
0 |
0 |
.... |
0 |
0 |
F(0,0,…,0,0) |
|
0 |
0 |
.... |
0 |
1 |
F(0,0,...,0,1) |
|
0 |
0 |
.... |
1 |
0 |
F(0,0, ....,1,0) |
|
.... |
.... |
.... |
.... |
.... |
.... |
|
1 |
1 |
1 |
1 |
1 |
F(1,1, …,1,1) |
Другой класс составляют ЛС с внутренней памятью, называемые последовательными; для них значения выходных логических переменных определяются не только текущими значениями входных переменных, но также их значениями в предыдущие моменты времени. Мы ограничимся рассмотрением только комбинационных ЛС, что вполне достаточно для иллюстрации рассматриваемой проблематики.
Логические переменные, объединенные знаками логических операций, составляют логические выражения. При вычислении значения логического выражения, как было отмечено ранее, определено следующее старшинство выполнения логических операций: сначала выполняется инверсия, затем конъюнкция и в последнюю очередь— дизъюнкция.
Для изменения указанного порядка используются скобки.
Например, значение логической функции трех переменных
f (x1, x2, x3) = (x1· x2 \/ х2 х3) x1 \/ x3
при наборе переменных (0, 1, 1) будет ложь, а при наборе (1, 0, 1) — истина.
Булевая алгебра позволяет не только проводить анализ ЛС, описываемых логическими выражениями или таблицами истинности, но и синтез их из более простых, т.е. решать в комплексе структурно-аналитические вопросы ЛС. Анализ ЛС состоит в установлении ее выходных значений по значениям логических входов, тогда как, соединяя известные ЛС в новую схему на основе описывающего ее логического выражения, производим синтез новых ЛС на основе уже имеющихся.
Элементарные ЛС, используемые при создании средств ЦВТ, называются вентилями (gates). В настоящее время существует целый ряд базовых вентилей, на основе которых строится современная ВТ; некоторые из них рассматриваются ниже. Так как набор {И, .ИЛИ, НЕ} логических операций является универсальным. (функционально полным), т.е. на его основе можно представлять любую логическую функцию, то соответствующий ему набор вентилей также будет универсальным:
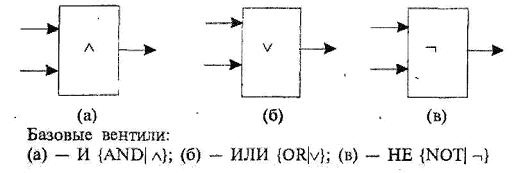
На основе базовых вентилей может быть построена любая ЛС; при этом вентили (а, б) могут иметь любое число входов, определяемое количеством переменных логического выражения, описывающего ЛС. Из математической логики известно, что наряду с (И, ИЛИ, НЕ) функционально полными являются и другие простые наборы базовых операций: (И, НЕ), {ИЛИ, НЕ} и другие.
С помощью логических схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у них бывают от двух до восьми входов и один или два выхода. Входные и выходные сигналы, соответствующие двум логическим состояниям в логических элементах — 1 и 0, имеют один из двух установленных уровней напряжения. Например, +5 Вольт и 0 Вольт. Высокий уровень обычно соответствует значению «истина» («1»), а низкий — значению «ложь» («О»).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию. Работу логических элементов описывают с помощью таблиц истинности.
Схема И. Эта схема реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах и таблица истинности схемы И с двумя входами представлены на рис. 4.4.
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль. Связь между выходом у этой схемы и входами х1 и х2 описывается соотношением: у = x1 x2 (читается как x1 и х2). Операция конъюнкции на структурных схемах обозначается знаком & (читается как «амперсэнд»), являющимся сокращенной записью английского слова «and».
Схема ИЛИ. Эта схема реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.
Условное обозначение на структурных схемах и таблица истинности схемы ИЛИ с двумя входами представлены на рис. 4.5. Знак 1 на схеме соответствует обозначению, т. е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1. Связь между выходом у этой схемы и входами x1 и х2 описывается соотношением: у = x1 х2 (читается как х1 или х2).
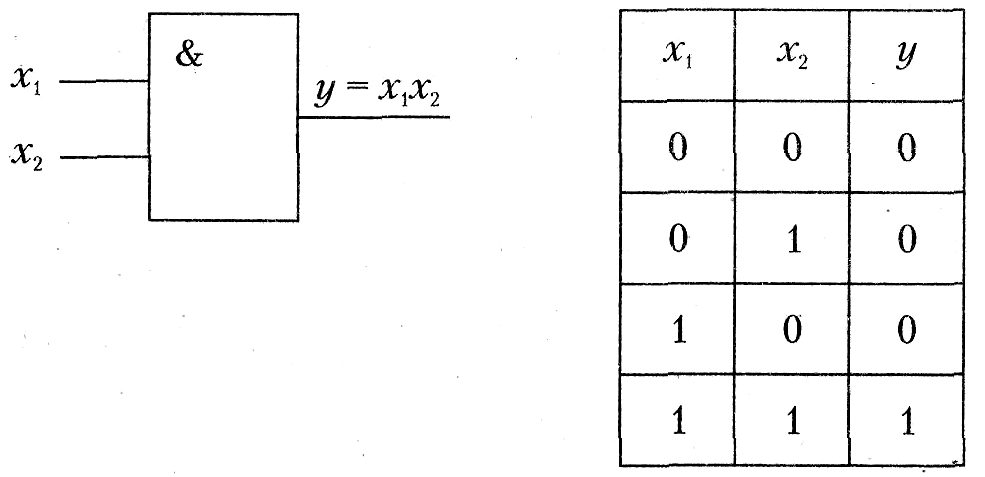
Рис. 4.4. Условное обозначение и таблица истинности схемы И
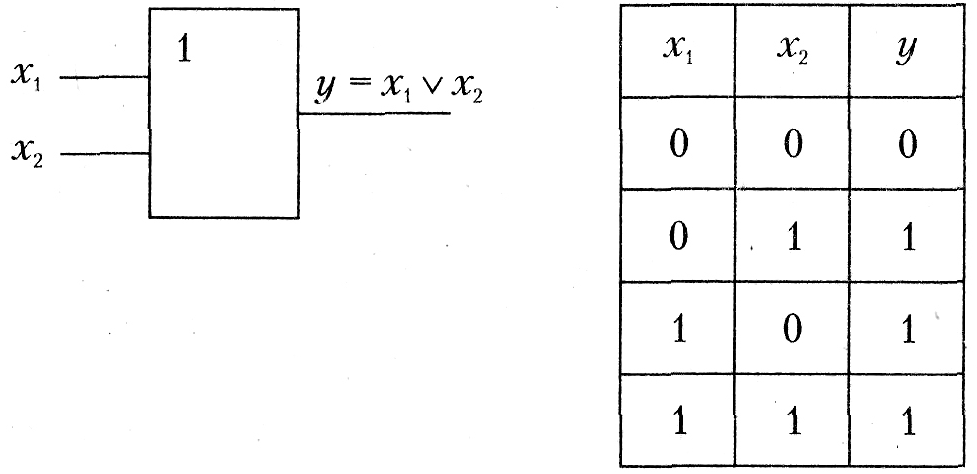
Рис. 4.5. Условное обозначение и таблица истинности схемы ИЛИ
Схема НЕ. Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом х этой схемы и выходом у можно записать соотношением у = ¯х , где ¯х читается как «не x» или «инверсия x».
Если на входе схемы 0, то на выходе 1. Когда на входе 1, то на выходе 0. Условное обозначение и таблица истинности инвертора представлены на рис. 4.6.
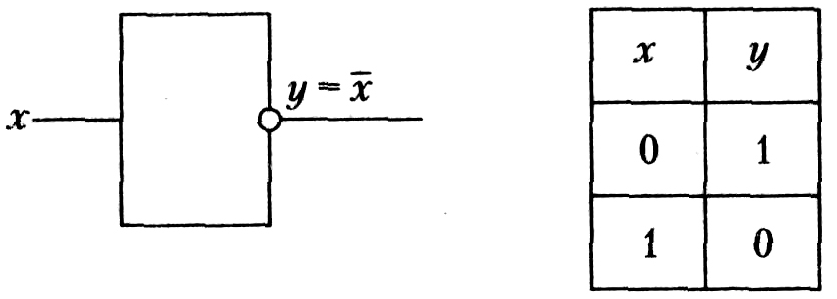
Рис. 4.6. Условное обозначение и таблица истинности схемы НЕ
Схема
И—НЕ.
Схема
состоит из элемента И и инвертора и
осуществляет отрицание результата
схемы И. Связь между выходом у
и
входами x1
и
х2
схемы
записывают следующим образом: у
=
![]() 1
1![]() 2,
где
2,
где
![]() 1
1![]() 2
читается
как «инверсия
x1
и
х2».
Условное
обозначение на структурных схемах и
таблица истинности схемы И—НЕ с двумя
входами представлены на рис. 4.7.
2
читается
как «инверсия
x1
и
х2».
Условное
обозначение на структурных схемах и
таблица истинности схемы И—НЕ с двумя
входами представлены на рис. 4.7.
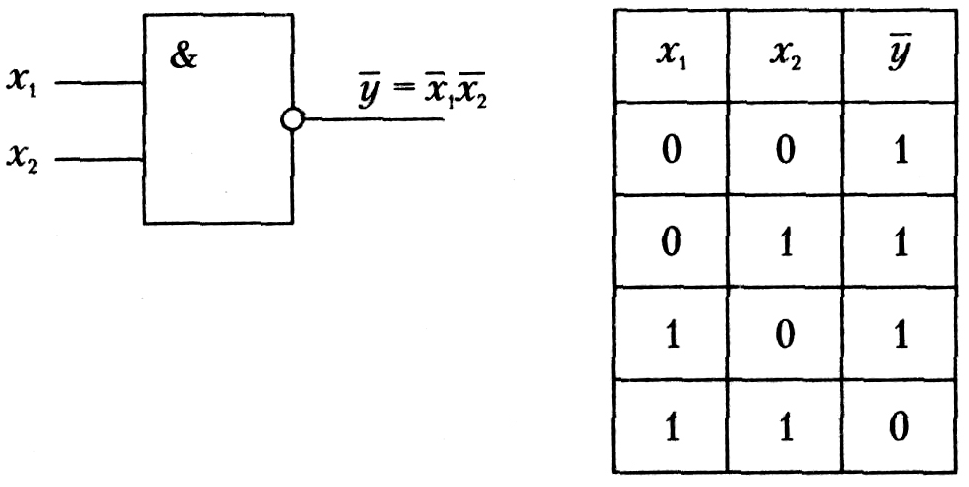
Рис. 4.7. Условное обозначение и таблица истинности схемы И—НЕ
Схема
ИЛИ—НЕ. Схема
состоит из элемента ИЛИ и инвертора и
осуществляет отрицание результата
схемы ИЛИ. Связь между выходом у
и
входами x1
и
х2
схемы
записывают следующим образом: у=![]() 1
1
![]() 2,
где
2,
где
![]() 1
1
![]() 2,
читается
как "инверсия
x1
или
х2".
Условное
обозначение на структурных схемах и
таблица истинности схемы ИЛИ—НЕ с
двумя входами представлены на рис. 4.8.
2,
читается
как "инверсия
x1
или
х2".
Условное
обозначение на структурных схемах и
таблица истинности схемы ИЛИ—НЕ с
двумя входами представлены на рис. 4.8.
Триггер (от англ. trigger—защелка, спусковой крючок) — электронное устройство с двумя устойчивыми состояниями равновесия, чередующимися под воздействием внешних сигналов, предназначенных для записи и хранения 1 бита данных.
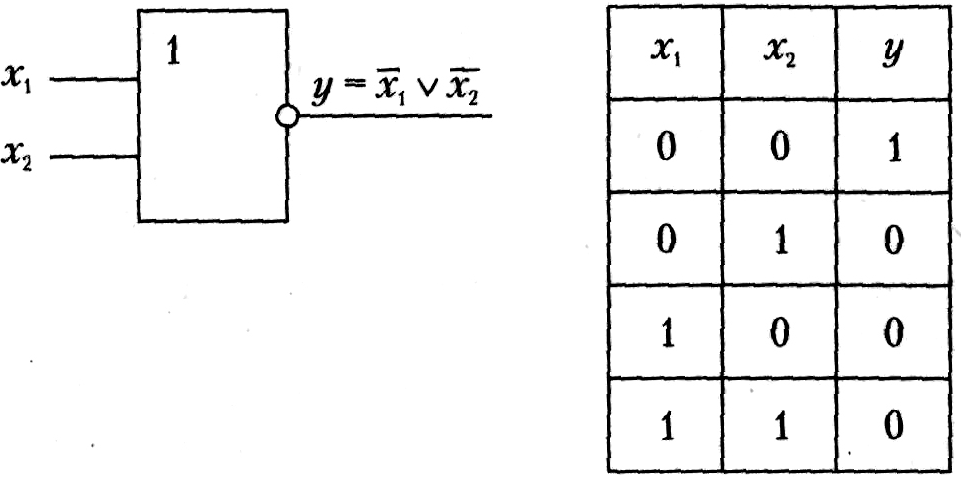
Рис. 4.8. Условное обозначение и таблица истинности схемы ИЛИ—НЕ
Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает «хлопанье».
В отличие от рассмотренных выше логических схем, триггеры — это логические устройства с памятью. Выходные сигналы триггеров в общем случае зависят не только от их входных сигналов, действующих в настоящий момент, но и от сигналов, действовавших на входы до этого (рис. 4.9).
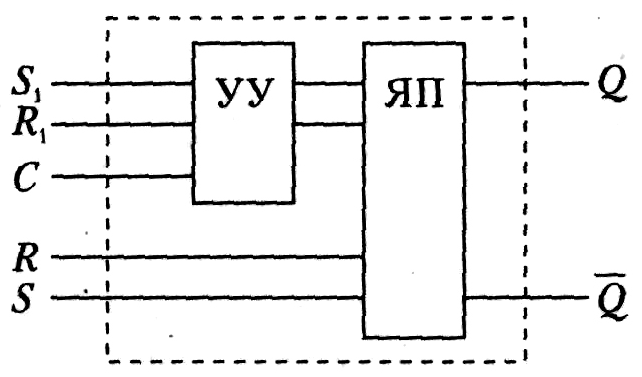
Рис. 4.9. Функциональная схема триггера
Триггер функционирует следующим образом. Устройство управления (УУ) преобразует входные сигналы так, что ячейка памяти (ЯП) принимает одно из двух устойчивых состояний в зависимости от входных сигналов. Входные сигналы поступают на входы S1 и R1 преобразуются устройством управления (УУ) и поступают на внутренние входы ячейки памяти (ЯП). В общем случае устройство управления может отсутствовать. Тогда сигналы подаются непосредственно на входы R и S ячейки памяти.
В триггерах также может осуществляться синхронизация приема информации с помощью входа С. При наличии входа С триггер называют синхронным, в противном случае — асинхронным.
В асинхронных триггерах информация может записываться непрерывно. В этом случае она определяется информационными сигналами, действующими на входах в данный момент времени, т. е. изменение состояния ячейки памяти происходит мгновенно после изменения состояния информационных входов.
В синхронном (или тактируемом) триггере информация заносится только в момент действия так называемого синхронизирующего сигнала. Синхронизация триггера может осуществляться как импульсом (потенциалом), так и фронтом (перепадом потенциала). В схемотехнике приняты следующие обозначения входов триггеров:
![]() — прямой
выход триггера;
— прямой
выход триггера;
![]() —инверсный выход
триггера;
—инверсный выход
триггера;
S — раздельный вход установки в единичное состояние (напряжение высокого уровня на прямом выходе Q);
R — раздельный вход установки в нулевое состояние (напряжение низкого уровня на прямом выходе Q);
D — информационный вход (на него подается информация, предназначенная для занесения в триггер);
С — вход синхронизации;
Т — счетный вход.
В основе любого триггера находится кольцо из двух инверторов (рис. 4.10). Это кольцо принято изображать в виде так называемой защелки (рис. 4.11).
Однозначную запись 1 бита информации в защелку можно осуществить, если снабдить ее цепями управления и запуска.
Схемы триггеров делятся на несколько типов: RS-, Т-, D-, JK-триггер и др. Состояние триггера определяется выходным Q(Q)'-сигналом, а правила его функционирования задаются таблицами переходов. Схема RS-триггера составляет основу для построения других типов триггеров.
Самый распространенный тип триггера — RS-триггер. Принципиальная схема RS-триггера (рис. 4.12) содержит защелку (два элемента И—НЕ или ИЛИ—НЕ), а также два раздельных статических входа управления. В зависимости от используемых элементов можно получить триггеры с прямыми входами (за активный логический уровень принимают уровень логической единицы) — элемент ИЛИ—НЕ — или с инверсными входами (за активный уровень принимается уровень логического ноля). Эти входы управления называют R (reset — сброс) и S (set — установка).
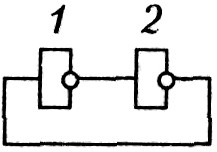
Рис. 4.10. Кольцо инверторов
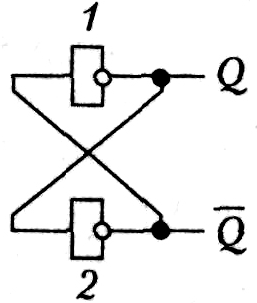
Рис. 4.11. Элемент-защелка
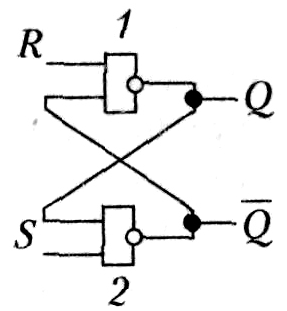
Рис. 4.12. Принципиальная схема RS-триггера
По сути дела, RS-триггер, изображенный на рис. 4.12, это триггер без устройства управления. Для триггера с прямыми входами подача на вход S-триггера логической единицы, а на вход R — логического ноля приведет к тому, что на выходе триггера Q установится сигнал единицы, и наоборот - при подаче на R единицы, а на S — ноля на выходе Q установится сигнал ноля. Таким образом, таблица истинности для данного триггера будет иметь вид, показанный в табл. 4.3.
Таблица 4.3

Как видно из табл. 4.3, комбинация R = 1 и S = 1 является запрещенной. После нее состояние выходов триггера становится неопределенным. На выходе Q может установиться как состояние логического ноля, так и состояние логической единицы.
Иногда режим работы триггера, при котором R = 1, a S = 0, называют режимом очистки, при R =0, S = 1 — режимом записи, а при R = 0, S = 0 — режимом хранения, так как информация на выходе триггера в этом случае не изменяется. Для триггера с инверсными входами таблица истинности имеет вид, представленный в табл. 4.4.
Таблица 4.4

Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно восемь триггеров, для запоминания килобайта соответственно 8 210 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
