
- •Информатика Учебное пособие
- •Содержание
- •Предисловие
- •Тема 1. Введение
- •1.1. Цель и задачи курса «Информатика»
- •1.2. Объекты и составные части информатики
- •1.3. Информатика как единство науки и технологии
- •Контрольные вопросы
- •Тема 2. Основные понятия информатики
- •2.1. Место информатики в системе наук
- •2.2. Основные понятия курса «Информатика»
- •Предмет информатики составляют следующие понятия:
- •Информация классифицируется по видам. (рис. 2.4.)
- •Тема 3. Основы дискретной математики.
- •3.2. Основы логики
- •Элементарные булевые функции
- •Из них выделим функцию "отрицание X" (обозначается -X). Эта функция представлена в таблице
- •3.3. Графы и деревья
- •А) граф g; б) остов графа g; в) другой остов графа g
- •Тема 4. Основные понятия архитектуры эвм
- •Для представления числовых данных в эвм используются естественная и нормальная формы записи чисел.
- •4.2. Системы счисления. Правила перевода чисел из одной системы счисления в другую
- •3. Арифметические операции
- •4.3. Логические элементы компьютера
- •В качестве важных последовательностных схем, выполняемых на одной ис, можно отметить счетчики, сдвиговые регистры, элементы памяти и др.
- •Структурная схема базовой модели мп фирмы Intel представлена на рисунке 4.15.
- •4.5. Организация памяти компьютера
- •Используется два основных типа оперативной памяти:
- •Контрольные вопросы
- •Тема 5. Алгоритмическое решение задач, анализ алгоритмической сложности.
- •5.1. Стратегия решения задач.
- •5.2. Алгоритмы (свойства, реализация алгоритмов)
- •5.3. Структуры данных
- •5.4. Основные вычислительные алгоритмы.
- •5.5. Анализ алгоритмов
- •1. Сравнительные оценки алгоритмов
- •2. Система обозначений в анализе алгоритмов
- •3. Классификация алгоритмов по виду функции трудоёмкости
- •4. Асимптотический анализ алгоритмов
- •Контрольные вопросы
- •Тема 6. Знакомство с языками программирования.
- •6.1. Обзор языков программирования
- •6.2. Основные конструкции программирования
- •Внутри программы значение свойств можно изменять как угодно часто.
- •Константы.
- •На практике наибольшее распространение получили язык функционального программирования lisp и два его диалекта: язык Common lisp и язык Scheme.
- •Наиболее распространенным языком логического программирования является язык Prolog (Пролог).
- •Контрольные вопросы
- •Тема 7. Основы операционных систем
- •7.1. Основные концепции операционных систем
- •7.4. Файловые системы
- •7.6. Обзор современного прикладного программного обеспечения
- •Контрольные вопросы
- •Тема 8. Сети и телекоммуникации
- •Компоненты сети
- •По программной совместимости эвм: однородные (гомогенные) и неоднородные (гетерогенные);
- •8.3. Системы телекоммуникаций
- •Типы телекоммуникационных систем
- •Системы телевещания
- •Системы подвижной связи
- •Сети сотовой подвижной связи
- •Сети транкинговой связи
- •Сети персонального радиовызова
- •Сети мобильной спутниковой связи
- •Волоконно-оптические сети
- •Контрольные вопросы:
- •Тема 9. Сеть Internet
- •9.1. Теоретические основы Internet
- •9.2. Основные понятия (сайт, сокет, сервер, клиент). Web как пример архитектуры «клиент-сервер»
- •9.3. Службы Internet
- •Контрольные вопросы:
- •Тема 10. Графическое программное обеспечение
- •10.1. Иерархия графического программного обеспечения. Графические коммуникации. Графические системы.
- •10.2. Системы растровой и векторной графики
- •Описание объекта является простым и занимает мало памяти;
- •10.3. Графические редакторы
- •Контрольные вопросы
- •Тема 11. Основы защиты информации
- •11.1. Информационная безопасность и ее составляющие
- •11.2. Угрозы безопасности информации и их классификация
- •11.3. Сетевая безопасность
- •11.4. Антивирусные программы
- •Контрольные вопросы
5.4. Основные вычислительные алгоритмы.
Алгоритмические (или вычислительные) процессы обработки данных делятся на виды:
- линейные,
- ветвящиеся,
- циклические.
Линейным называется такой вычислительный процесс, в котором самостоятельные этапы вычислений выполняются в последовательности их записи, т.е. в естественном порядке.
Каждая операция является самостоятельной, независимой от каких-либо условий.
Линейные вычислительные процессы имеют место при вычислении арифметических выражений.
Пример 1:
![]()
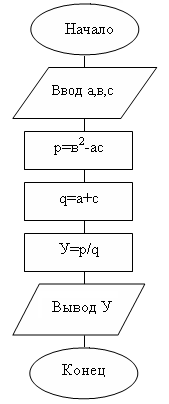
Ветвящимся называется такой процесс, в котором его реализация происходит по одному из нескольких заранее предусмотренных (возможных) направлений в зависимости от исходных условий или промежуточных результатов. Каждое отдельное направление вычислений в таком процессе называется ветвью вычисления. Выбор осуществляется проверкой выполнения логического условия.
В каждом конкретном случае обработки данных вычислительный процесс выполняется лишь по одной ветви, а выполнение остальных – исключается.
Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей- сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.
Направления ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» - условие выполнено, «нет» -условие не выполнено.
Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса.
Пример 2:
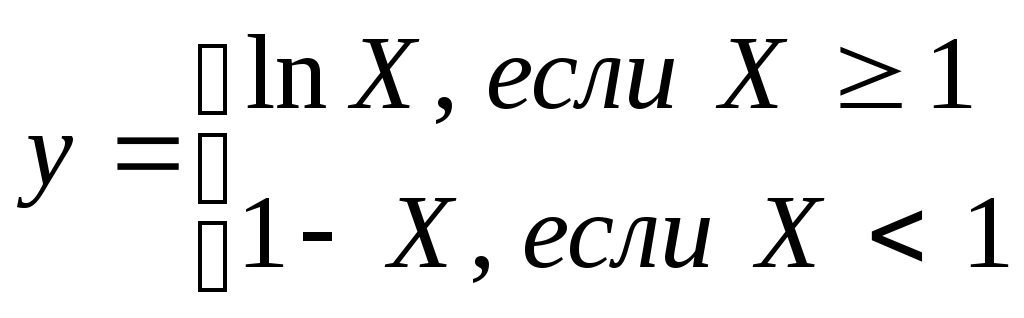

При реализации алгоритмов многих задач наблюдается многократное повторение отдельных этапов их вычислительного процесса. Такие многократно повторяемые этапы вычислений называются циклами, а вычислительные процессы, содержащие многократно повторяемые этапы называются циклическими.
Пример 3:
У=X20

5.5. Анализ алгоритмов
Целью анализа трудоемкости алгоритмов является нахождение оптимального алгоритма для решения данной задачи. В качестве критерия оптимальности алгоритма выбирается трудоемкость алгоритма, понимаемая как количество элементарных операций, которые необходимо выполнить для решения задачи с помощью данного алгоритма. Функцией трудоемкости называется отношение, связывающие входные данные алгоритма с количеством элементарных операций.
Трудоёмкость алгоритмов по-разному зависит от входных данных. Для некоторых алгоритмов трудоемкость зависит только от объема данных, для других алгоритмов — от значений данных, в некоторых случаях порядок поступления данных может влиять на трудоемкость. Трудоёмкость многих алгоритмов может в той или иной мере зависеть от всех перечисленных выше факторов.
1. Сравнительные оценки алгоритмов
При использовании алгоритмов для решения практических задач мы сталкиваемся с проблемой рационального выбора алгоритма решения задачи. Решение проблемы выбора связано с построением системы сравнительных оценок, которая в свою очередь существенно опирается на формальную модель алгоритма.
Будем рассматривать в дальнейшем, придерживаясь определений Поста, применимые к общей проблеме, правильные и финитные алгоритмы, т.е. алгоритмы, дающие j-решение общей проблемы. В качестве формальной системы будем рассматривать абстрактную машину, включающую процессор с фонНеймановской архитектурой, поддерживающий адресную память и набор «элементарных» операций соотнесенных с языком высокого уровня.
В целях дальнейшего анализа примем следующие допущения:
- каждая команда выполняется не более чем за фиксированное время;
- исходные данные алгоритма представляются машинными словами по β битов каждое.
Конкретная проблема задается N словами памяти, таким образом, на входе алгоритма - Nβ=N•β бит информации. Отметим, что в ряде случаев, особенно при рассмотрении матричных задач N является мерой длины входа алгоритма, отражающей линейную размерность.
Программа, реализующая алгоритм для решения общей проблемы состоит из М машинных инструкций по βм битов - Мβ=М•βм бит информации.
Кроме того, алгоритм может требовать следующих дополнительных ресурсов абстрактной машины:
- Sα— память для хранения промежуточных результатов;
- Sγ— память для организации вычислительного процесса (память, необходимая для реализации рекурсивных вызовов и возвратов).
При решении конкретной проблемы, заданной N словами памяти алгоритм выполняет не более, чем конечное количество «элементарных» операций абстрактной машины в силу условия рассмотрения только финитных алгоритмов. В связи с этим введем следующее определение:
Под трудоёмкостью алгоритма для данного конкретного входа - Fα(N), будем понимать количество «элементарных» операций, совершаемых алгоритмом для решения конкретной проблемы в данной формальной системе.
Комплексный анализ алгоритма может быть выполнен на основе комплексной оценки ресурсов формальной системы, требуемых алгоритмом для решения конкретных проблем. Очевидно, что для различных областей применения веса ресурсов будут различны, что приводит к следующей комплексной оценке алгоритма:
ΨA=С1 • Fα(N)+ С2 •М+ С3 •Sα+ С4 • Sγ, где Сi - веса ресурсов.
