Пример 12.
Найти собственные числа и собственные векторы оператора:
Решение.
Составим и решим характеристическое уравнение:
(2-
)(-3-
)(-2-
)
+ 3 + 0 – 2 (-3-
)(-1)
– 0 – 5(-1)(-2-
)
= 0.
(4-
2)
(3+
)
+ 3 – 6 – 2
- 10 - 5
= 0.
-
3
- 3
2+ 4
+ 12 - 7
- 13 = 0.
3
+ 3
2+ 3
+ 1 = 0.
(
+1)3
= 0.
= -1, следовательно,
собственное число
имеет кратность 3.
Решим систему уравнений (*).
,
,
– любое действительное число, не равное
нулю.
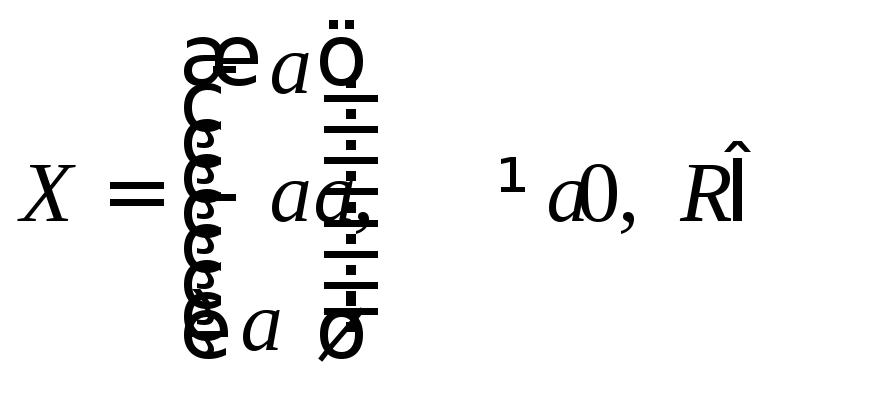–собственные
векторы, соответствующие собственному
числу
.
Пример 13.
Найти собственные числа и собственные векторы оператора
Решение.
Составим и решим характеристическое уравнение
,
разложив определитель по третьему
столбцу.
(3-
)((2-
)2-1)
= 0
(3-
)(
2-
4
+3) = 0
(3-
)(3-
)(1-
)
= 0
= 3,
= 1,
= 3 – собственные числа.
Решим систему
уравнений (*)для
.
=>
–любые действительные
числа.
Обозначим
,
тогда собственным числам
соответствуют собственные векторы
.
Условие
означает, что
.
Найдем собственные
векторы для
.
Решим систему уравнений (*).
=>
=>
=>
=>
Пусть
,
тогда
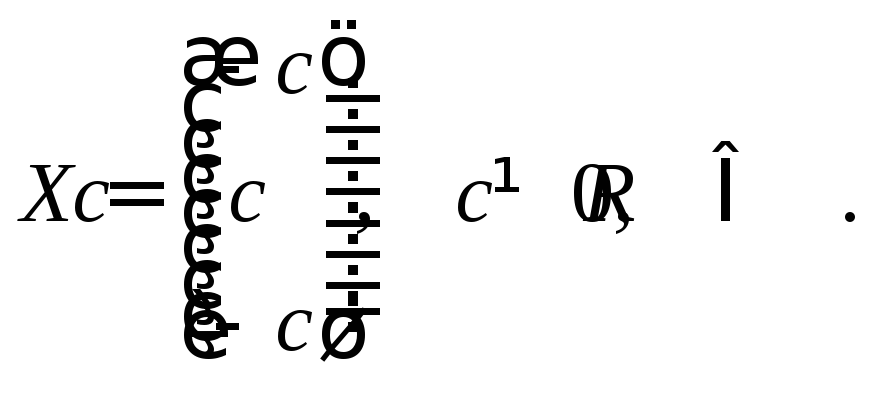
Ответ:собственному числу
соответствуют собственные векторы
,
собственным
числам
соответствуют собственные векторы
.
7. Операции над векторами
При сложении двух векторов их соответствующие координаты складываются. При умножении вектора на число все его координаты умножаются на это число. Например, если:
Скалярное произведение двух векторов равно сумме произведений одноименных координат. Т.е., если
Например, если
то
.
Пример 14.
Вычислить
если
Решение.
8. Разложение вектора по базису
Пример 15.
Даны векторы x1, x2, x3 и y. Требуется:
а) показать, что векторы x1, x2, x3 образуют базис трехмерного пространства;
б) найти координаты вектора y в этом базисе.
Систему линейных уравнений решить методом Крамера.
Решение.
Для того чтобы показать, что векторы x1, x2, x3 образуют базис трехмерного пространства, нужно показать их линейную независимость, то есть показать, что определитель, составленный из координат векторовx1, x2, x3, не равен нулю.
векторы x1, x2, x3 линейно независимы, то есть образуют базис трехмерного пространства.
Пусть вектор yимеет координаты (y1,y2,y3)в базисеx1, x2, x3. Это означает, чтоy=y1x1 +y2 x2 +y3 x3. В координатной форме это имеет вид:
(3,0,-1) = y1(3,1,4) +y2(2,-1,-2) +y3(1,0,1).
При умножении вектора на число все его координаты умножаются на это число; при сложении векторов складываются их соответствующие координаты. Таким образом,
(3,0,-1) = (3y1,y1,4y1) + (2y2,-y2,-2y2) + (y3,0,y3) =
=( 3y1+2y2+y3,y1-y2+0, 4y1-2y2+y3).
Два вектора равны, если равны их соответствующие координаты. Приравнивая координаты, получим систему уравнений.
Решим систему методом Крамера:
Здесь
-определитель, составленный из
коэффициентов при неизвестных.
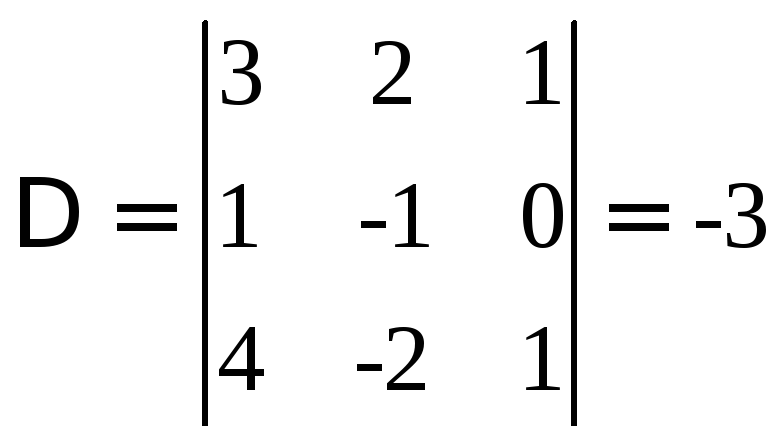
Чтобы получить
определители
нужно в определителе
заменитьi-ый столбец
на столбец свободных членов.
y1 =(- 4)/(-3) = 4/3.
y2 = (-4)/(-3) = 4/3,
y3 = 11/(-3) = -11/3, то естьy = (4/3, 4/3, -11/3).
Содержание
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ 3
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ 4
ЗАДАНИЕ 1: Вычислить произведение матриц. 4
ЗАДАНИЕ 2: Решить систему линейных алгебраических уравнений методом Гаусса. 6
ЗАДАНИЕ 3: Вычислить определитель двумя способами: 9
ЗАДАНИЕ 4: Решить матричное уравнение. 11
ЗАДАНИЕ 5: Найти ранг системы векторов. 13
ЗАДАНИЕ 6. Найти собственные значения и собственные векторы оператора, заданного матрицей. 15
x2= (1; 2; 3) x2= (2; -3; 0) x2= (1; 2; 4) 18
x3= (2; 0; -1) x3= (1; 0; -1) x3= (2; 1; 1) 18
x3= (2; 1; 1) x3= (3; 2; 1) x3= (1; 2; -3) 18
x3= (2; 0; 2) x3= (2; 1; 1) x3= (2; 0; 3) 18
x3= (3; 2; -2) x3= (2; 2; 1) x3= (1; 1; -1) 19
y = (4; -1; 2) y = (2; 3; -2) y = (1; 0; 3) 19
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ 20
1. ОПЕРАЦИИ НАД МАТРИЦАМИ 20
2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ГАУССА 22
3. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ 30
4. РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ 36
5. ВЫЧИСЛЕНИЕ РАНГА СИСТЕМЫ ВЕКТОРОВ 39
6. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ ЛИНЕЙНОГО ОПЕРАТОРА 44
7. ОПЕРАЦИИ НАД ВЕКТОРАМИ 48
8. РАЗЛОЖЕНИЕ ВЕКТОРА ПО БАЗИСУ 49