Методические указания к решению задач

1. Операции над матрицами

Матрицейназывается прямоугольная таблица чисел.

Две матрицы называются равными, если они имеют одинаковое количество строк и столбцов, и на соответствующих местах у них находятся равные элементы.Сложениеопределяется только для матриц имеющих одинаковое число строк и одинаковое число столбцов, при этом складываются их соответствующие элементы. Например:

Чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на это число. Например:

называется транспонированной матрицейдля матрицыА. При транспонировании матрицы, строки и столбцы меняются местами. Например:

.

Чтобы умножить матрицу А на матрицу В необходимо, чтобы число столбцов матрицы А равнялось числу строк матрицы В. При этом элемент матрицы произведения, стоящий на пересечении к-ой строки и n-го столбца, равен сумме парных произведений элементов к-ой строки матрицы А на соответствующие элементы n-го столбца матрицы В. Например,

Заметим, что, вообще говоря, AB BA.

В матрице ABстолько же строк, сколько их в матрицеA,и столько же столбцов, сколько их в матрицеB.

Пример 1

Найти матрицу , если

3 5 -6 9 0 3

А= 2 7 0 , В= -2 4 1 .

-1 1 4 5 7 8

Найдём матрицу , для этого поменяем местами строки и столбцы матрицы А.

3 2 -1

= 5 7 1 .

-6 0 4

Теперь найдём произведение :

3 2 -1 9 0 3

= 5 7 1 -2 4 1 =

-6 0 4 5 7 8

3·9 +2·(-2)+(-1)·5 3·0+2·4+(-1)·7 3·3+2·1+(-1)·8

= 5·9 +7·(-2)+ 1·5 5·0+7·4+1·7 5·3+7·1+1·8 =

-6·9 +0·(-2)+ 4·5 -6·0+0·4+4·7 -6·3+0·1+4·8

18 1 3

= 36 35 30 .

-34 28 14

Прибавим к полученной матрице матрицу А.

18 1 3 3 5 -6 18+3 1+5 3-6

= 36 35 30 + 2 7 0 = 36+2 35+7 30+0 =

-34 28 14 -1 1 4 -34-1 28+1 14+4

21 6 -3

= 38 42 30

-35 29 18

2. Решение систем линейных алгебраических уравнений методом гаусса

При решении системы линейных алгебраических уравнений методом Гаусса составляют расширенную матрицу этой системы и приводят её к ступенчатому виду. Для этого можно менять местами строки матрицы, умножать все элементы строки на одно число, прибавлять к строке другую строку, умноженную на некоторое число.

Пример 2

Решить систему линейных алгебраических уравнений методом Гаусса

2x + у + 3z = 0

x – 2y – 2z = 1

3x + 3y – z = 7

Расширенная матрица системы будет иметь вид:

Поменяем местами первую и вторую строки. Получим эквивалентную матрицу.

Здесь мы умножили первую строку на (-2) и прибавили ко второй. Затем умножили первую строку на (-3) и прибавили к третьей. В результате матрица приняла вид:

Теперь нужно получить нуль на месте цифры девять. Чтобы не иметь дела с дробями, умножим вторую строку на два, а затем вычтем из неё третью строку. После этого умножим вторую строку на (-9) и прибавим к третьей.

~ ,

Итак, матрица приведена к ступенчатому виду. Запишем уравнение, соответствующее последней строке полученной матрицы,

-76 z = 76. Тогда z = -1.

Запишем уравнение, соответствующее второй строке матрицы,

y + 9 z = -8.

Подставим найденное значение z = -1 и найдём у.

y – 9 = - 8, у = 1.

Подставляя у = -1 и z = -1 в первое уравнение x-2у-2z =1, найдём x.

x-2+2=1, х=1.

Т.е. x =1, у =1, z = -1 - решение системы.

Не всегда система линейных алгебраических уравнений имеет единственное решение. Рассмотрим решение системы в таких случаях.

Пример 3

Решить систему линейных алгебраических уравнений методом Гаусса

2x + 3у – z = 0

x – y + 3z = 1

4x + y + 5z = 2 .

Запишем расширенную матрицу системы и приведём её к ступенчатому виду.

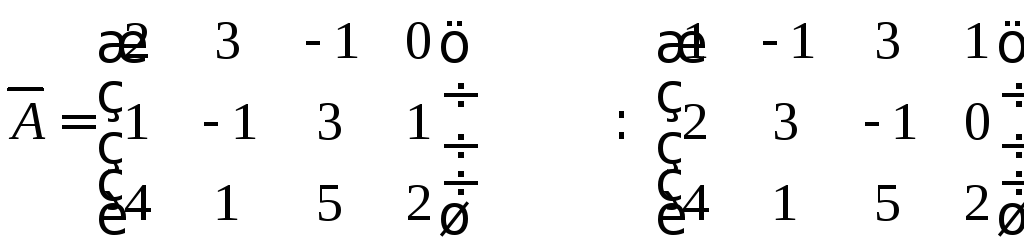
Здесь мы сначала поменяли местами первую и вторую строки, затем первую строку умножили на (-2) и прибавили ко второй строке, потом первую строку умножили на (-4) и прибавили к третьей. В результате получилась матрица с двумя равными строками. Умножили вторую строку на (-1) и прибавили к третьей. Получили матрицу с нулевой строкой.

Запишем уравнение, соответствующее второй строке матрицы, и выразим из него у через z:

5y - 7z = -2, y = (7z - 2)/5.

Первой строке матрицы соответствует уравнение x – y + 3z = 1. Подставим в уравнение у и выразим x через z. Приведем к общему знаменателю:

x = (3 – 8z)/5 .

Итак, данная система имеет бесконечное множество решений. Все они могут быть записаны в виде общего решения:

x = (3 – 8z)/5

y = (7z – 2)/5

z - любое действительное число.

Придавая z конкретные значения, можно получить частные решение этой системы. Например, если z = 1, то x = -1, у = 1.

Замечание: Из уравнения 5y – 7z = -2 мы выразили y через z, тем самым, положив z свободной переменной (т.е. z может принимать любые действительные значения), а у – базисной. Можно было z выразить через y. В этом случае y являлась бы свободной переменной, а z – базисной. В этом случае z = (5y + 2)/7. Подставим z в первое уравнение

x– y + 3 z = 1.

.

Приведем к общему знаменателю:

Так как переменная y объявлена свободной, то выражаем x через y:

7x = 1– 8y, x = (1 – 8y)/7.

В этом случае общее решение будет иметь вид:

x = (1 – 8 y )/7

y – любое действительное число

z = (5y +2)/7.

Пример 4

Решить систему линейных алгебраических уравнений методом Гаусса

2x + 3y – 2z = 3

x – 2y + 3z = 0

3x + y + z = 5.

Приведём расширенную матрицу системы к ступенчатому виду.

2 3 -2 3 1 -2 3 0

~ 1 -2 3 0  2 3 -2 3 

3 1 1 5 3 1 1 5

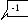1 -2 3 0 1 -2 3 0

~ 0 7 -8 3 ~ 0 7 -8 3

0 7 -8 5 0 0 0 -2 .

Уравнение, соответствующее последней строке матрицы, имеет вид: 0 = -2, что невозможно ни при каких значениях х, у, z. Т.е., система решений не имеет.

Пример 5

Решить систему линейных алгебраических уравнений методом Гаусса

x₁ + x₂ – x₃ – 2x₄ = 1

2x₁ + 3x₂ – 2x₃ – 4x₄ = 3

x₁ + 2x₂ – x₃ – 2x₄ = 2

3x₁ + 5x₂ – 3x₃ – 6x₄ = 5 .

Проведем расширенную матрицу системы к ступенчатому виду

~

~~

~ .

Из уравнения, соответствующего второй строке , находим. Запишем уравнение, соответствующее первой строке, и подставим в него:

Так как ни одну из переменных не объявляли свободной или базисной, то выразим, например,черези:.

Теперь и – свободные переменные, – базисная.

Общее решение будет иметь вид:

Замечание: Если при выборе свободных и базисных переменных возникают затруднения, то в преобразованной матрице А отбрасывают все нулевые строки и столбец свободных членов. В оставшейся матрице рассматривают определители максимального размера. Если определитель не равен нулю, то переменные, соответствующие его столбцам, можно взять в качестве базисных.

В предыдущем примере

.

Отбросим нулевые строки и столбец свободных членов (последний). Получили матрицу .

Рассмотрим все возможные определители второго порядка. (Индексы указывают переменные, соответствующие столбцам определителей).

, ,,

, ,.

Так как после преобразований осталось два уравнения с четырьмя переменными, то две переменные будут базисными, а две – свободными.

Поскольку пары(х₁, х₃), (х₁, х₄)_, (х₃, х₄) брать в качестве базисных нельзя. А пары (х₁, х₂), (х₂, х₃)_, (х₂, х₄) можно.

Это соответствует тому, что – базисная переменная, а в первом уравнении после подстановки любую переменную можно взять в качестве базисной, то есть выразить через две другие. Общее решение в каждом случае будет свое.