Математическая статистика:

Тема : Вариационные ряды и их характеристики.

Задача 1. Для заданной выборки:

1. построить дискретный ряд распределения, составить таблицу частот;

2. построить полигон частот, кумуляту;

3. вычислить среднее значение 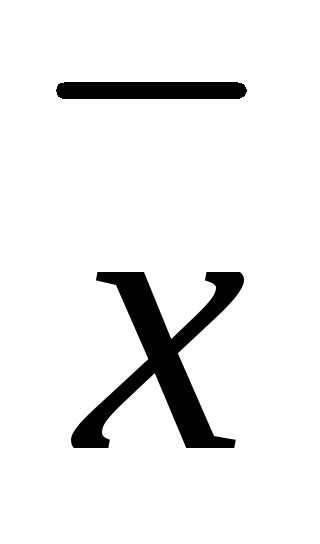, дисперсию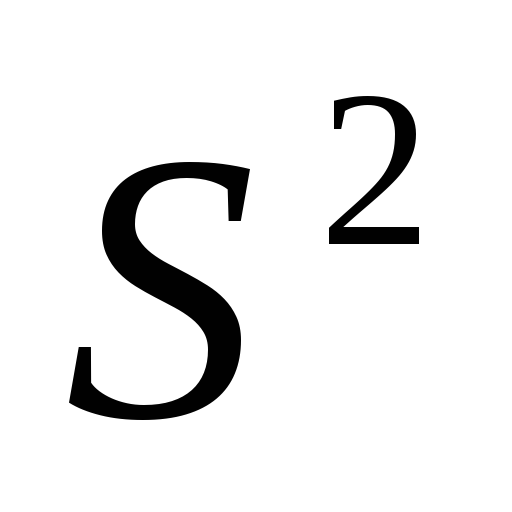и среднеквадратическое отклонение.

Элементы выборки:

2	4	4	1	5	1	8	1	3	9	4	2	1	7
7	3	7	8	7	3	2	3	5	3	8	2	6	6
3	5	2	8	3	7	9	5	8	8	1	5	1

Решение.

1). Для построения дискретного ряда распределения располагаем различные значения признака Х в порядке их возрастания и для каждого из этих значений определяем его частоту, а также относительную частоту (частость ). Результаты группировки сводим в таблицу. Кроме перечисленных характеристик вычисляем накопленные частоты:

№ п/п	Варианта	Частота	Частость	Накоплен ная частота	Накоплен ная частость
1	1	6	0,146	6	0,146
2	2	5	0,122	11	0,268
3	3	7	0,171	18	0,439
4	4	3	0,073	21	0,512
5	5	5	0,122	26	0,634
6	6	2	0,049	28	0,683
7	7	5	0,122	33	0,805
8	8	6	0,146	39	0,951
9	9	2	0,049	41	1
Итого		41	1

2). Построим полигон частот. Для этого по оси абсцисс откладываем варианты (), а по оси ординат – соответствующие им частоты (). Полученные на пересечении абсцисс и ординат точки соединяем прямыми линиями, в результате получаем ломаную линию, которая называетсяполигоном частот:

Если по оси ординат отложить относительные частоты, то получим полигон относительных частот.

33

28

26

3). Определим статистические показатели ряда распределения.

Среднее арифметическое признака определяется по формуле:

, где - объем вариационного ряда.

Выборочная дисперсия:

Среднеквадратическое отклонение:

.

Тема : Проверка статистических гипотез.

Задача 2. По заданной выборке проверить гипотезу о нормальном распределении случайной величины по критерию согласия Пирсона. Произвести интервальную оценку выборочного среднего значения с доверительной вероятностью 0,98. Выборка: =182

58	60	63	64	65	67	68	69	70	70	72	73	73	74
79	8	82	82	83	84	85	85	86	88	89	90	93	95
68	68	70	70	72	72	73	73	74	74	75	77	77	78
84	85	86	86	88	90	91	94	95	57	58	60	64	64
73	73	74	75	75	77	77	78	78	79	80	80	82	82
93	94	96	57	62	65	65	68	69	70	72	73	74	75
85	85	88	88	90	98	103	55	59	62	62	63	64	65
72	72	73	73	74	74	75	75	77	77	78	78	78	79
84	84	85	86	86	88	89	90	90	91	94	99	101	75
62	63	65	80	82	82	69	70	72	86	88	77	78	75
69	70	72	67	69	80	84	75	83	74	89	83	79	65
82	59	85	80	70	83	77	57	77	100	83	82	80	68
80	68	89	83	82	78	67	79	67	79	79	79	78	69

Решение. Для построения интервального ряда распределения определим число групп в ряду распределения по формуле Г.А. Стерджесса:

.

Принимаем число интервалов .

Максимальное значение ряда 103, минимальное значение ряда 55.

Длина интервала: .

Центр распределения: .

Поскольку число интервалов нечетное, центр распределения находится в центре среднего интервала.

Полученный ряд распределения: (52-58); (58-64); (64-70); (70-76); (76-82); (82-88); (88-94); (94-100); (100-106).

Принимаем гипотезу , утверждающую, что случайная величинаимеет нормальный закон распределения. В качестве критерия для проверки этой гипотезы используем случайную величину– критерий согласия Пирсона, который имеет приближенное распределение с числом степеней свободы. Здесь– число интервалов, на которые разделена область изменения; – количество неизвестных параметров теоретического распределения, оценки которых вычисляются по выборке; – объем выборки; - эмпирические частоты;- теоретические частоты, где- вероятность попадания значения признакав-й интервал. Чтобы утверждение о распределении случайной величины по законубыло достаточно точным, требуется выполнение условия. В случае невыполнения условия для некоторых интервалов, их объединяют с соседними интервалами.

Теоретические частоты вычислим по формулам: , где,- значения функции Лапласа (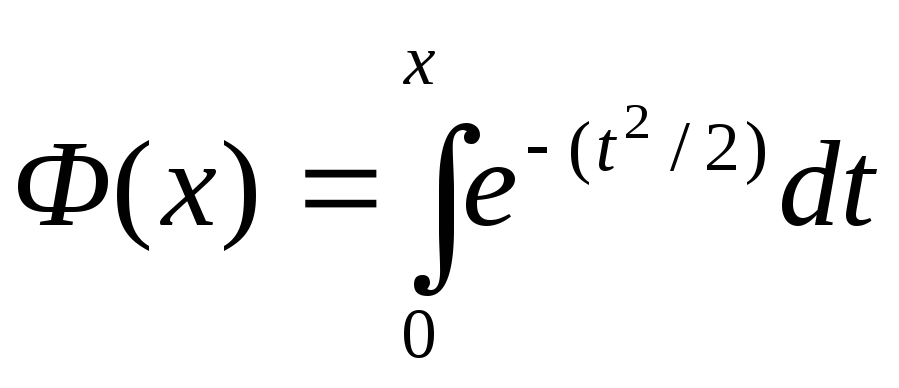– находится по таблице).

Левый конец первого интервала принимаем равным – , а правый конец последнего интервала + .

Определим эмпирические частоты и характеристики выборки:

№ n/n	Интервалы	Частоты	Середины интервалов
1	52-58	4	55	-21,53	2045,82
2	58-64	13	61	-15,53	3588,92
3	64-70	26	67	-9,53	2929,85
4	70-76	42	73	-3,53	894,67
5	76-82	34	79	2,47	65,18
6	82-88	33	85	8,47	1799,57
7	88-94	19	91	14,47	3403,81
8	94-100	8	97	20,47	3006,11
9	100-106	3	103	26,47	1933,14
		182			19667,08

Характеристики выборки рассчитываются по следующим формулам:

Выборочное среднее

Выборочная дисперсия

.

Среднеквадратическое отклонение:

.

Определим доверительный интервал для . Интервальной оценкой (с надежностью) математического ожиданиянормально распределенного количественного признакапо выборочной среднейпри неизвестном среднем квадратическом отклонениигенеральной совокупности служит доверительный интервал:

< a <, гдеS – «исправленное» выборочное среднее квадратическое отклонение

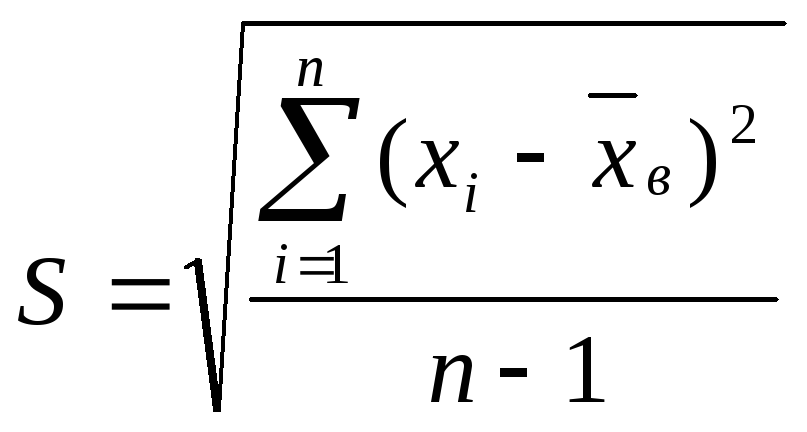, находят по таблице критических точек распределения Стьюдента по заданному числу степеней свободыи уровню значимости. Для= 0,98 (и=182:.

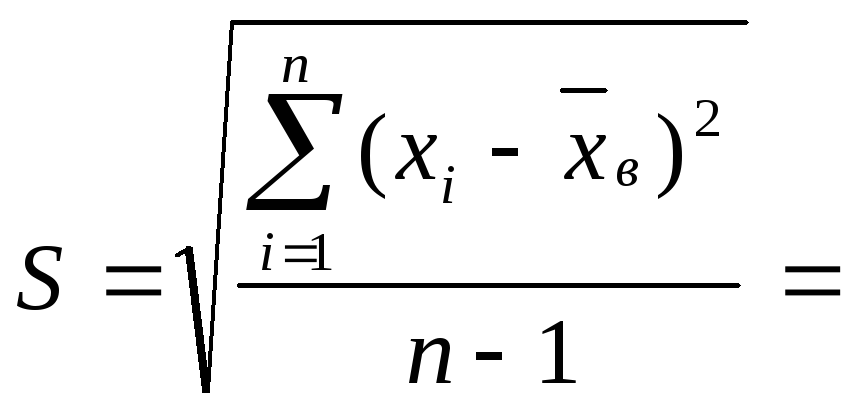
< <, отсюда

75,82 < < 79,42.

Таким образом, интервалом, покрывающим с вероятностью 0,98, служит интервал (75,82; 79,42).

Для вычисления теоретических характеристик учитывая, что ,,, составим расчетную таблицу:

	Границы интервала
1		58		-1,887	-0,5	-0,4706	5,3508	4
2	58	64	-1,887	-1,310	-0,4706	-0,4049	11,957	13
3	64	70	-1,310	-0,733	-0,4049	-0,2673	25,043	26
4	70	76	-0,733	0,155	-0,2673	-0,0636	37,073	42
5	76	82	0,155	0,422	-0,0636	0,1628	41,205	34
6	82	88	0,422	0,999	0,1628	0,3413	32,487	33
7	88	94	0,999	1,576	0,3413	0,4429	18,491	19
8	94	100	1,576	2,153	0,4429	0,4846	7,5894	8
9	100		2,153		0,4846	0,5	2,8028	3
∑							182,00	182

Поскольку для последнего интервала теоретическая частота меньше 5, объединим два последних интервала в один и на основании полученных величин найдем расчетное значение критерия Пирсона.

	Границы интервала
1		58	5,3508	4	0,341007
2	58	64	11,9574	13	0,090907
3	64	70	25,0432	26	0,036555
4	70	76	37,0734	42	0,654685
5	76	82	41,2048	34	1,259784
6	82	88	32,487	33	0,008101
7	88	94	18,4912	19	0,014000
8	94		10,3922	11	0,035548
∑			182,00	182	2,440587

=2,44.

Для определения критического значения критерия Пирсона найдем число степеней свободы:

.

Здесь – число групп ряда распределения в последней таблице;– число параметров нормального закона распределения, оценки которых вычислялись по выборке.

По таблице критических точек распределения для уровня значимости 0,02 и числа степеней свободы 5 находим

.

Поскольку <, то значениене принадлежит критической области и, следовательно, гипотеза о нормальном распределении генеральной совокупностипринимается.