Перпендикуляр и наклонная

Теорема. Если из одной точки вне плоскости проведены перпендикуляр и наклонные, то:

1) наклонные, имеющие равные проекции, равны;

2) из двух наклонных больше та, проекция которой больше;

3) равные наклонные имеют равные проекции;

4) из двух проекций больше та, которая соответствует большей наклонной.

Теорема о трех перпендикулярах. Для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна проекции наклонной (рис. 12.3).

Теорема о площади ортогональной проекции многоугольника на плоскость. Площадь ортогональной проекции многоугольника на плоскость равна произведению площади многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.

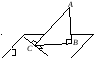
Рис. 12.3

Пример 1. Через данную точку провести прямую, параллельную данной плоскости.

Р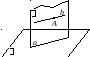ешение. Анализ. Предположим, что прямая построена (рис. 12.4). Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в плоскости (по признаку параллельности прямой и плоскости). Две параллельные прямые лежат в одной плоскости. Значит, построив плоскость, проходящую через данную точку и произвольную прямую в данной плоскости, можно будет построить параллельную прямую.

Рис. 12.4

Построение.

1. На плоскости  проводим прямую а.

2. Прямая а и точка А задают плоскость. Построим плоскость .

3. В плоскости  через точку А проведем прямую b, параллельную прямой а.

4. Построена прямая b, параллельная плоскости .

Доказательство. По признаку параллельности прямой и плоскости прямая b параллельна плоскости , так как она параллельна прямой а, принадлежащей плоскости .

Исследование. Задача имеет бесконечное множество решений, так как прямая а в плоскости  выбирается произвольно.

Пример 2. Определите, на каком расстоянии от плоскости находится точка А, если прямая АВ пересекает плоскость под углом 45º, расстояние от точки А до точки В, принадлежащей плоскости, равно см.

Решение.Сделаем рисунок (рис. 12.5):

Рис. 12.5

АС – перпендикуляр к плоскости , АВ – наклонная, угол АВС – угол между прямой АВ и плоскостью . Треугольник АВС – прямоугольный, так какАС – перпендикуляр. Искомое расстояние от точки А до плоскости – это катет АС прямоугольного треугольника. Зная угол и гипотенузу найдем катетАС:

В ответе получаем: АС = 3 см.

Пример 3. Определите, на каком расстоянии от плоскости равнобедренного треугольника находится точка, удаленная от каждой из вершин треугольника на 13 см, если основание и высота треугольника равны по 8 см.

Решение. Сделаем рисунок (рис. 12.6). Точка S удалена от точек А, В и С на одинаковое расстояние. Значит, наклонные SA, SB и SC равные, SO – общий перпендикуляр этих наклонных. По теореме о наклонных и проекциях АО = ВО = СО.

Точка О – центр окружности, описанной около треугольника АВС. Найдем ее радиус:

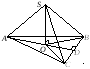
Рис. 12.6

где ВС – основание; AD – высота данного равнобедренного треугольника.

Находим стороны треугольника АВС из прямоугольного треугольника ABD по теореме Пифагора:

Теперь находим ОВ:

Рассмотрим треугольник SOB: SB = 13 см, ОВ = 5 см. Находим длину перпендикуляра SO по теореме Пифагора:

В ответе получаем: SO = 12 см.

Пример 4. Даны параллельные плоскости  и . Через точку М, не принадлежащую ни одной из них, проведены прямые а и b, которые пересекают плоскость  в точках А₁ и В₁, а плоскость  – в точках А₂ и В₂. Найти А₁В₁, если известно, что МА₁ = 8 см, А₁А₂ = 12 см, А₂В₂ = 25 см.

Решение. Так как в условии не сказано, как расположена относительно обеих плоскостей точка М, то возможны два варианта: (рис. 12.7, а, б). Рассмотрим каждый из них. Две пересекающиеся прямые а и b задают плоскость. Эта плоскость пересекает две параллельные плоскости  и  по параллельным прямым А₁В₁ и А₂В₂ согласно теореме 5 о параллельных прямых и параллельных плоскостях.

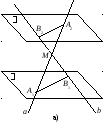
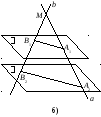
Рис. 12.7

Треугольники МА₁В₁ и МА₂В₂ подобны (углы А₂МВ₂ и А₁МВ₁ – вертикальные, углы МА₁В₁ и МА₂В₂ – внутренние накрест лежащие при параллельных прямых А₁В₁ и А₂В₂ и секущей А₁А₂). Из подобия треугольников следует пропорциональность сторон:

Отсюда

Вариант а):

Вариант б):

Получаем ответ: 10 см и 50 см.

Пример 5. Через точку А плоскости  проведена прямая АВ, образующая с плоскостью угол . Через прямую АВ проведена плоскость , образующая с плоскостью  угол . Найти угол между проекцией прямой АВ на плоскость  и плоскостью .

Решение. Сделаем рисунок (рис. 12.8). Из точки В опустим перпендикуляр на плоскость . Линейный угол двугранного угла между плоскостями и  – это угол ПрямаяAD перпендикулярна плоскости треугольника DBC, по признаку перпендикулярности прямой и плоскости, так как иПо признаку перпендикулярности плоскостей плоскость перпендикулярна плоскости треугольника DBC, так как она проходит через прямую AD. Искомый угол построим, опустив перпендикуляр из точки С на плоскость , обозначим его Найдем синус этого угла прямоугольного треугольникаСАМ. Введем вспомогательный отрезок ВС = а. Из треугольника АВС: Из треугольникаВМС ( ) найдем:

Тогда искомый угол

Рис. 12.8

Получаем ответ:

Задания