I уровень
1.1.Решите уравнение:
1)
2)
3)
4)
1.2.Решите задачу Коши:
1)
2)
3)
4)
II уровень
2.1.Решите уравнение:
1)
2)
3)
4)
2.2.Решите задачу Коши:
1)
2)
3)
III уровень
3.1.Составьте линейное дифференциальное уравнение по его фундаментальной системе решений:
1)
2)
3)
4)
3.2.Докажите,
что функции
образуют фундаментальную систему
решений уравнения
Проверьте:
1) являются ли
решениями данного уравнения функции
2) имеет ли данное уравнение действительные решения.
22.7. Линейные неоднородные дифференциальные
уравнения
Линейным неоднородным дифференциальным уравнением n-го порядка называется уравнение вида
(22.58)
где
– непрерывные функции на некотором
промежутке (a, b).
Если
в уравнении (22.58), то получаемсоответствующее
однородное дифференциальное уравнение
(22.59)
Общее решение уравнения (22.58) определяется формулой
(22.60)
где 
– общее
решение соответствующего однородного
уравнения,
– частное решение неоднородного
уравнения.
Для решения дифференциального уравнения (22.58) используют метод Лагранжа(метод вариации произвольных постоянных). Для его реализации необходимо сделать следующее:
1. Записать соответствующее однородное дифференциальное уравнение.
2. Найти фундаментальную систему частных решений
соответствующего однородного дифференциального уравнения.
3. Найти общее решение однородного уравнения в виде
(22.61)
где
– константы.
4. Решение заданного
неоднородного дифференциального
уравнения искать в виде (22.61), но считать,
что
– функциональные коэффициенты, которые
надо найти.
5. Для нахождения
коэффициентов
решения уравнения (22.61) необходимо
записать систему уравнений
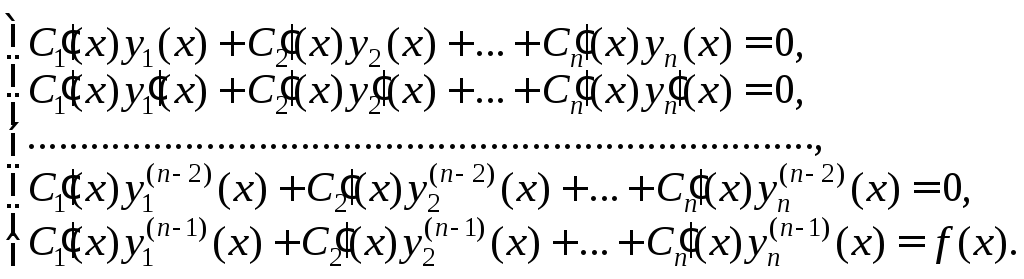(22.62)
6. Решить систему
(22.62) относительно
и получить
7. Проинтегрировать
полученные равенства для
и найти
где
– произвольные постоянные.
8. Подставить
полученные выражения вместо
в записанное решение (22.61). Это и есть
общее решение заданного дифференциального
уравнения (22.58).
Согласно методу
Лагранжа, сразу находим общее решение
(22.60) заданного дифференциального
уравнения (22.58) (без нахождения отдельно
его частного решения
).
Для решения линейных неоднородных дифференциальных уравнений (22.58) с постоянными коэффициентами и правой частью f(x) специального вида используютметод Эйлера(метод неопределенных коэффициентов). Этот метод применим, если функцияf(x) имеет вид:
(22.63)
где
– многочлены степениnиmсоответственно.
Для реализации метода необходимо сделать следующее:
1. Решить соответствующее однородное дифференциальное уравнение (22.59), используя характеристическое уравнение:
(22.64)
Общее решение дифференциального уравнения (22.59) записать в виде
(22.65)
где
– частные решения уравнения (22.59),
полученные в соответствии с типом корней
характеристического уравнения (22.64).
2. Записать
контрольное число
где
– числа, которые заданы в (22.63). Определить,
имеется ли число
среди корней уравнения (22.64). Если имеется,
то какова кратностьkэтого корня.
3. Если
не содержится среди корней характеристического
уравнения (22.64), то записать искомое
частное решение
дифференциального уравнения (22.58) в виде
(22.66)
Если среди корней
характеристического уравнения (22.64)
имеется корень
кратность которогоk,
то искомое частное решение
дифференциального уравнения (22.58)
записать в виде
(22.67)
где в равенствах
(22.66) и (22.67)
– многочлены степениr,
– бóльшая степень заданных многочленов
в (22.63). Многочлены
и
необходимо записать в стандартном виде
с буквенными коэффициентами.
4. Коэффициенты
многочленов
найти методом неопределенных коэффициентов.
Для этого необходимо вычислить производные
функции (22.66) или (22.67) и подставить в
левую часть уравнения (22.58). Далее надо
привести подобные относительно
и
а затем приравнять многочлены при
одноименных тригонометрических функциях.
Используя равенство многочленов,
записывают систему уравнений относительно
искомых числовых коэффициентов.
5. Найденные значения
числовых коэффициентов необходимо
подставить в многочлены
и
частного решения
,
записанного в виде функции (22.66) или
(22.67).
6.
Записать общее решение заданного
дифференциального уравнения (22.58) в виде
(22.60), где решение
имеет вид (22.65),а
– решение вида, записанного в предыдущем
5-м «шаге».
З
а м е ч а н и е 1. Форма записи (22.66) или
(22.67) сохраняется и в случаях, когда в
исходном уравнении (22.58)
или
гдеa, b
– числа. Тогда
гдеA, B
– числа, которые надо найти.
З а м е ч а н и е 2. Если правая часть уравнения (22.58) есть сумма различных функций специального вида, то для нахождения yч используют теорему о наложении решений: если в уравнении (22.58) правая часть имеет вид:
где
а
– частные решения уравнений
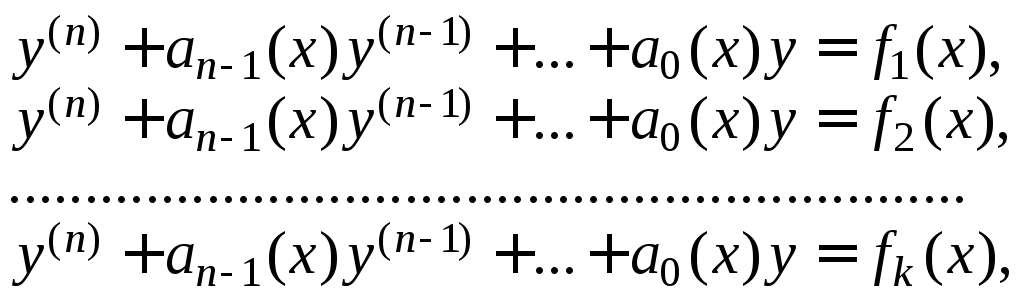
соответственно, то функция
является решением заданного уравнения.
3. Если
в правой части f(x)
уравнения (22.58) присутствует только одно
слагаемое с тригонометрической функцией
(т. е.
или
),
то общее решение и в этом случае записывают
в виде (22.66) или (22.67), т. е.
с двумя тригонометрическими функциями.
Пример 1. Решить уравнение методом Лагранжа:
1)
2)
3)
Решение.
1) Это неоднородное линейное дифференциальное
уравнение 2-го порядка. Найдем решение
соответствующего однородного уравнения
Его
характеристическое уравнение
корни которого
– комплексно-сопряженные, простые.
Тогда общее решение
соответствующего однородного уравнения
где C1, C2
– произвольные постоянные.
Общее решение заданного дифференциального уравнения ищем в виде
(22.68)
где
– функции, которые надо найти.
Для нахождения C1(x), C2(x) решим систему уравнений
Используем, например, метод Крамера:
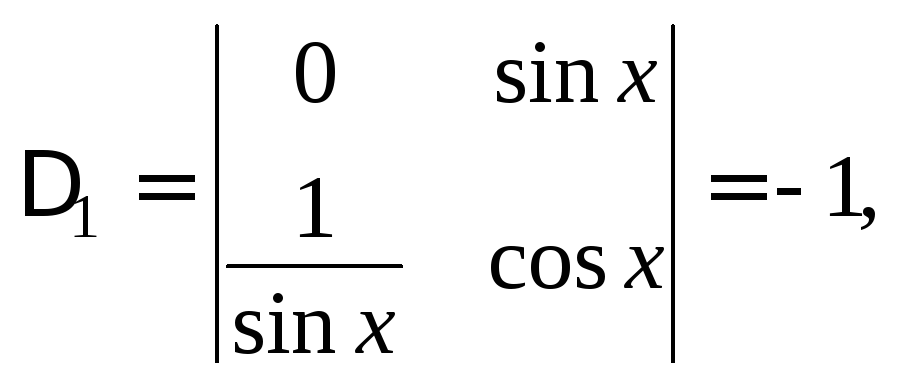
Тогда решениями системы будут:
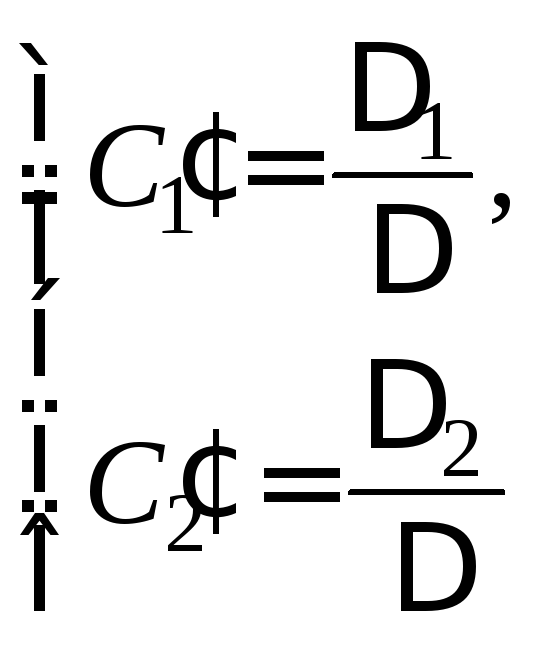или
Интегрируя полученные равенства, получаем:
где
– произвольные постоянные.
Подставляем найденные значения функций в (22.68) и получаем общее решение заданного дифференциального уравнения:
2)
Это неоднородное линейное дифференциальное
уравнение 2-го порядка. Найдем решение
соответствующего однородного уравнения:
Его характеристическое уравнение
корни которого
– простые, действительные. Тогда общее
решение соответствующего однородного
уравнения
где
– произвольные постоянные.
Общее решение заданного дифференциального уравнения ищем в виде
(22.69)
где
– функции, которые надо найти.
Для
нахождения
решим систему уравнений
Используем метод Крамера:
Тогда решение системы:
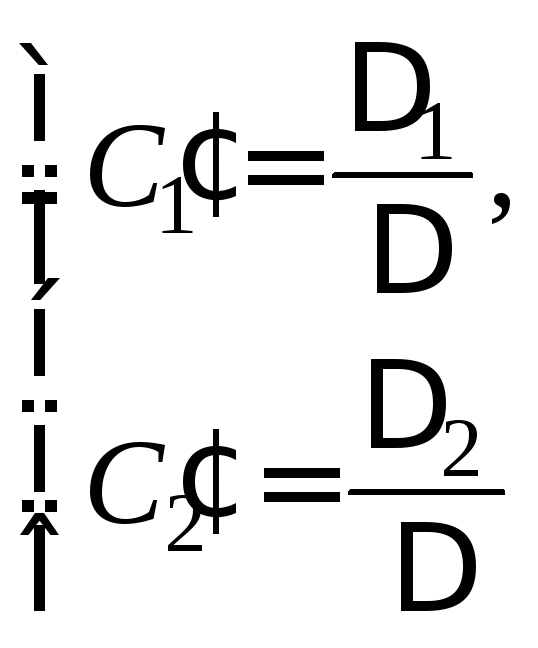или
Интегрируем полученные равенства:
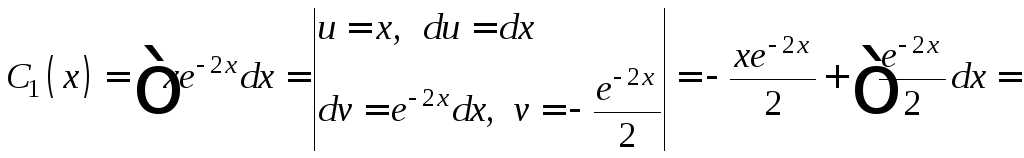
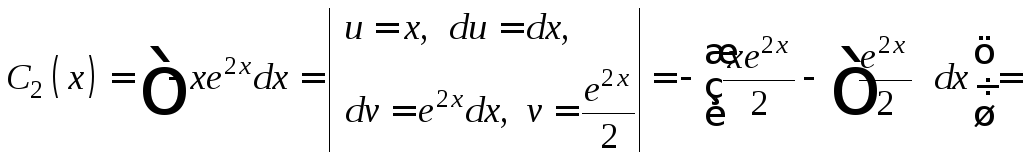
Таким образом,
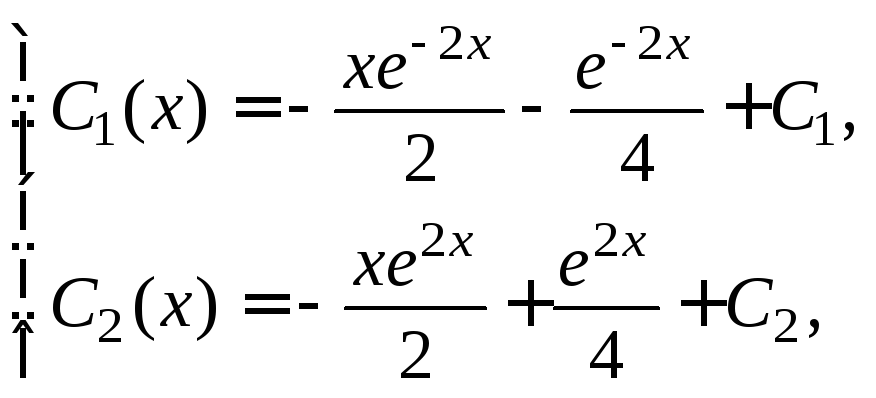
где
– произвольные постоянные. Подставляем
найденные значения функций в (22.69) и
получаем общее решение заданного
дифференциального уравнения:
После упрощения приходим к ответу:
3) Это неоднородное линейное дифференциальное уравнение 3-го порядка. Найдем решение соответствующего однородного уравнения
Его
характеристическое уравнение
корни которого
– действительные, простые. Тогда общее
решение соответствующего однородного
уравнения
где
– произвольные постоянные. Общее решение
заданного дифференциального уравнения
ищем в виде
(22.70)
где
– функции, которые надо найти. Для
нахождения
решаем систему уравнений
По методу Крамера:
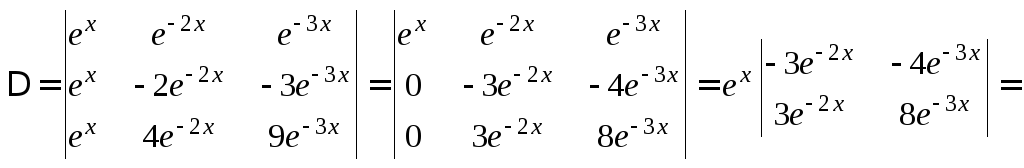
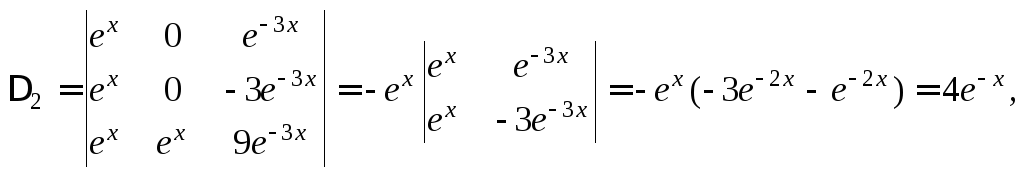
Тогда решение системы:
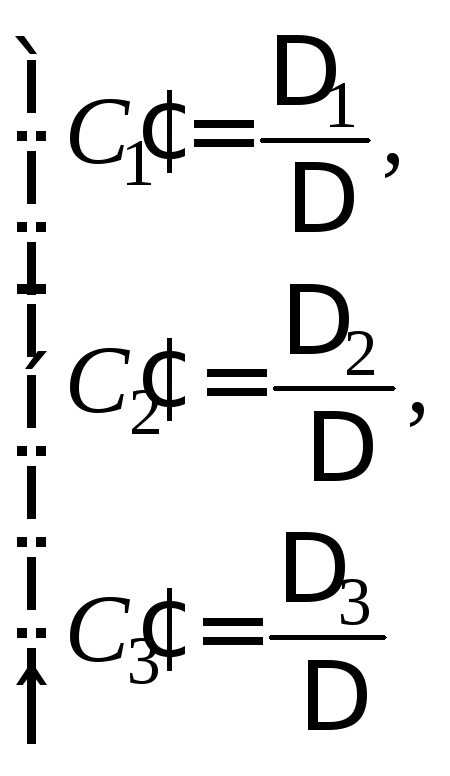или
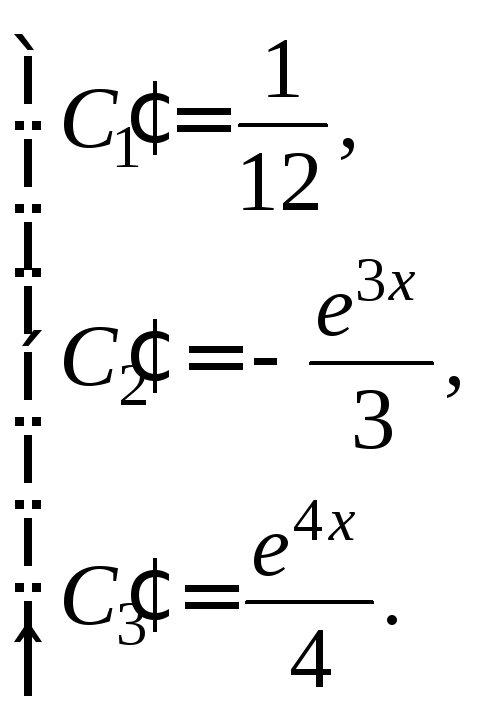
Интегрируя полученные равенства, получаем:
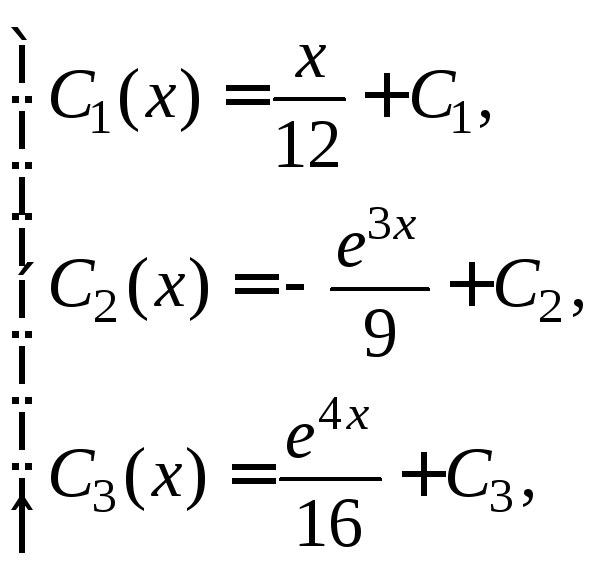
где
– произвольные постоянные.
Подставляем найденные значения функций в (22.70) и получаем общее решение заданного дифференциального уравнения:
После упрощения приходим к ответу:
Пример 2. Решить задачу Коши:
1)
2)
Решение.
1) Это линейное неоднородное дифференциальное
уравнение 2-го порядка. Найдем общее
решение соответствующего однородного
уравнения
Его характеристическое уравнение
корни которого
– комплексно-сопряженные, простые.
Тогда общее решение соответствующего
однородного уравнения
Общее решение заданного дифференциального
уравнения ищем в виде
где
– функции, для нахождения которых
составляем систему
Решаем ее методом Крамера:
Получаем решение системы:
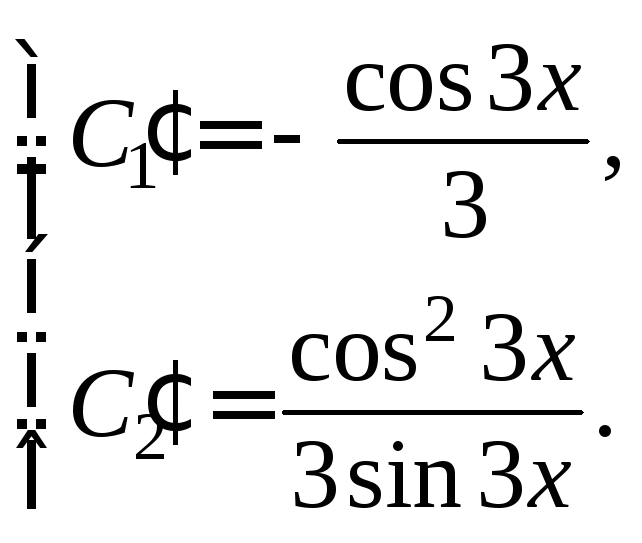
Интегрируем полученные равенства:
где
– произвольные постоянные.
Тогда общее решение заданного дифференциального уравнения:
После упрощения получаем:
Далее решаем задачу Коши. Дифференцируем полученное общее решение:
Подставляем
начальные условия
в выражения дляy
и
и определяем константы
и
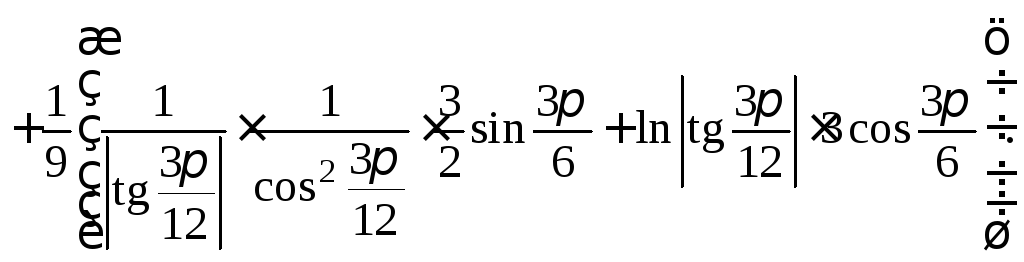
Отсюда имеем:
Получаем решение задачи Коши:
2)
Это линейное неоднородное дифференциальное
уравнение 3-го порядка. Найдем его общее
решение методом Лагранжа. Соответствующее
однородное уравнение имеет вид:
Его характеристическое уравнение
где
– корни. Тогда общее решение однородного
дифференциального уравнения:
Общее решение заданного дифференциального уравнения ищем в виде
где
– искомые функциональные коэффициенты.
Составляем систему
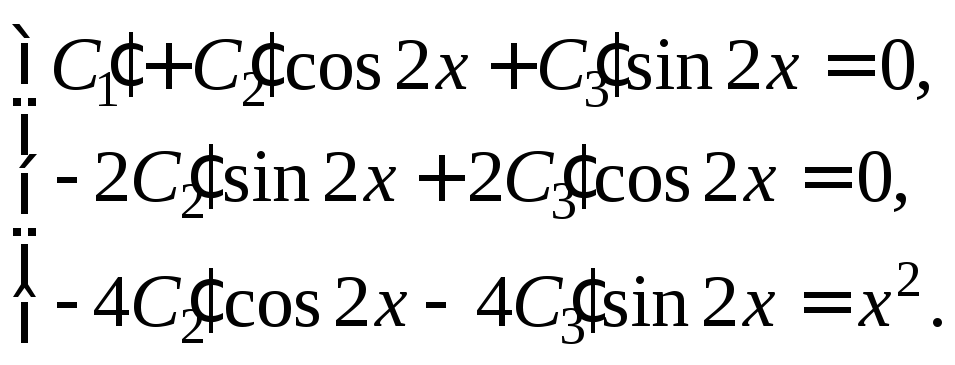
Решаем ее методом Крамера:
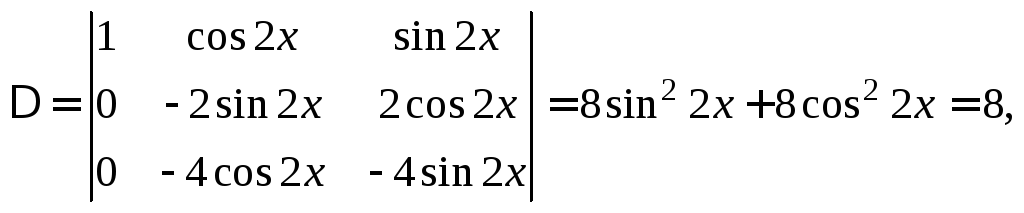
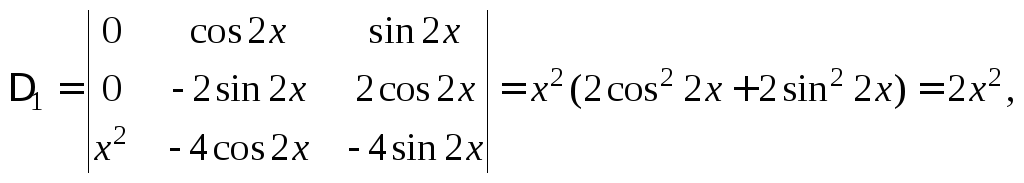
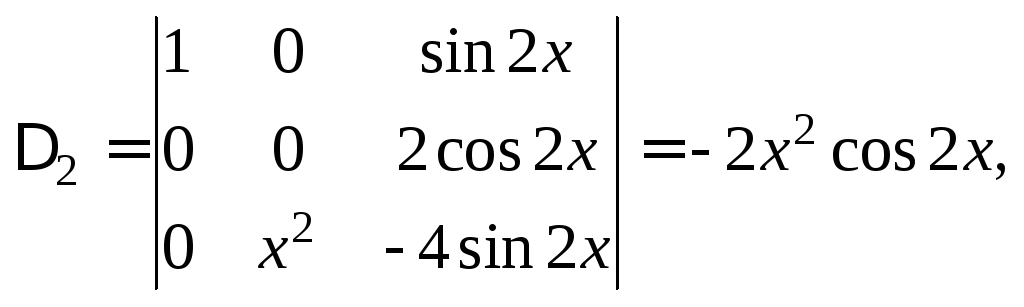
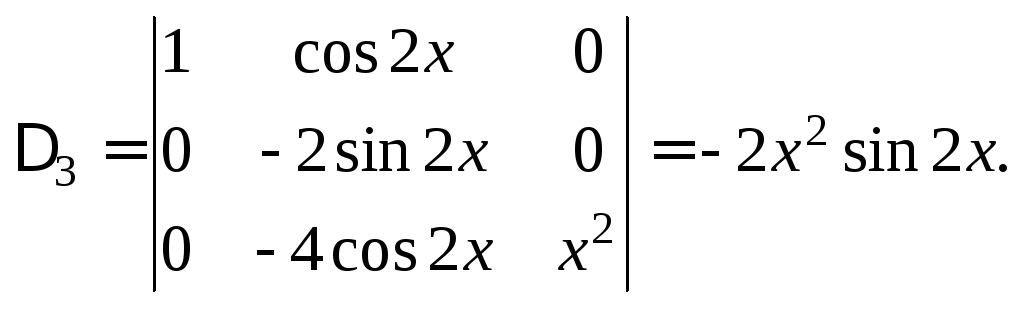
Тогда решение системы:
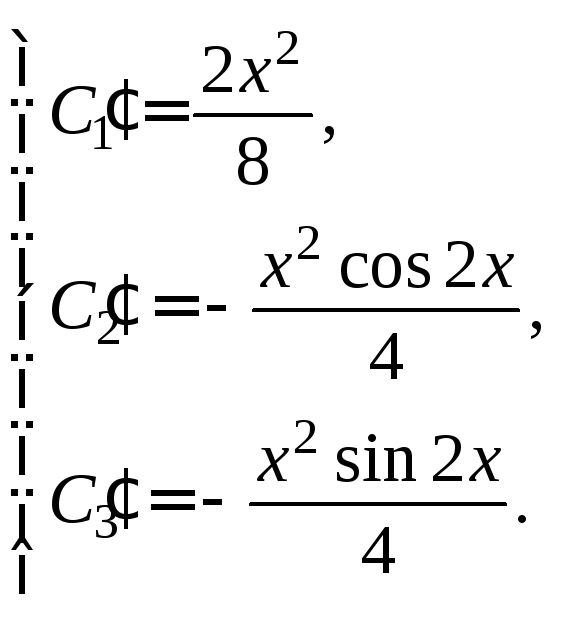
Интегрируем эти равенства:
где
– произвольные постоянные (при
интегрировании
и
применялся метод интегрирования по
частям).
Подставляя
выражения для
в общее решение, получаем:
или после упрощения:
Дифференцируем полученное общее решение дважды:
Подставляем
в выражения для
заданные начальные условия и находим
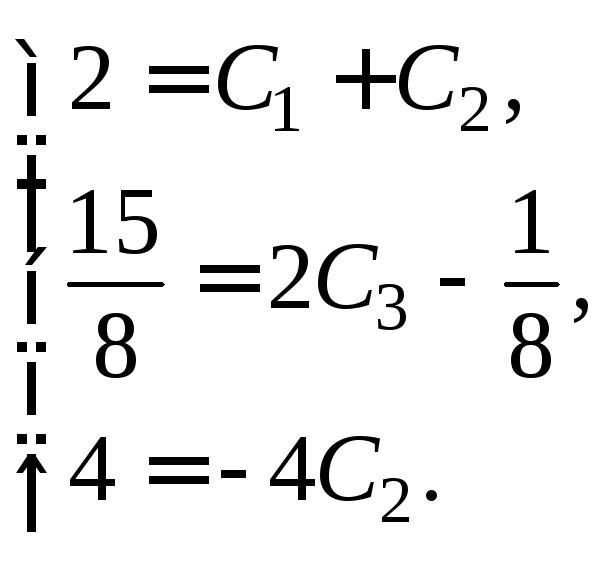
Отсюда
Получили решение задачи Коши:
Пример 3. Решить уравнение:
1)
2)
3)
Решение. 1) Это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами и правой частью специального вида. Для его решения используем метод Эйлера.
Рассмотрим
соответствующее однородное уравнение
Его характеристическое уравнение
корни которого
– действительные, простые.
Тогда общее решение соответствующего однородного уравнения:
где
– произвольные постоянные. Запишем
контрольное число
(так как
).
Контрольное число не содержится среди
корней характеристического уравнения.
Тогда искомое частное решение заданного
дифференциального уравнения имеет вид:
где A, B, C – неопределенные коэффициенты, которые надо найти.
Вычислим
производные
Подставляем
полученные выражения
и
в заданное дифференциальное уравнение:
Сокращаем
на
и группируем относительно степенейx:
Приравниваем коэффициенты при одинаковых степенях x:
Решаем полученную систему уравнений и находим A, B, C:
Подставляем найденные коэффициенты в частное решение:
или
Тогда общее решение заданного дифференциального уравнения имеет вид:
2)
Это линейное неоднородное дифференциальное
уравнение 4-го порядка с постоянными
коэффициентами и правой частью
специального вида. Используем метод
Эйлера для нахождения его общего решения.
Соответствующее однородное уравнение
–
Его характеристическое уравнение
или
корни
которого
кратности 2 (комплексно-сопряженные).
Тогда общее решение соответствующего однородного уравнения:
где
– произвольные постоянные.
Запишем
контрольное число
так как
Контрольное число
содержится среди корней характеристического
уравнения кратности 2. Поэтому искомое
частное решение заданного дифференциального
уравнения ищем в виде
где A, B – коэффициенты, которые надо найти.
Дифференцируем
дважды:
Упростим
Далее получим:
Упростим это выражение:
Дифференцируем еще раз:
Упрощаем это выражение:
Подставляем
выражения для
и
в заданное дифференциальное уравнение:
Группируем
относительно
и
После преобразований в скобках получим:
Приравниваем коэффициенты при одноименных тригонометрических функциях и получаем систему
решение
которой:
Подставляем
найденные коэффициенты в частное решение
Тогда общее решение заданного дифференциального уравнения:
или
3)
Это линейное неоднородное дифференциальное
уравнение 3-го порядка с постоянными
коэффициентами и специальной правой
частью. Соответствующее однородное
уравнение –
Его характеристическое уравнение
или
Получаем
корни характеристического уравнения
Общее решение соответствующего однородного уравнения имеет вид:
где
– произвольные постоянные.
Запишем
контрольное число
так как
Контрольное число не содержится среди
корней характеристического уравнения.
Тогда искомое частное решение заданного
дифференциального уравнения ищем в
виде
где
A, B, C, D
– коэффициенты, которые надо найти.
Дифференцируем трижды
Упростим это выражение:
Далее дифференцируем:
Упростим это выражение:
Упростим это выражение:
Подставляя
выражения для
в заданное дифференциальное уравнение,
группируем и, приравнивая коэффициенты
при одноименных тригонометрических
функциях, имеем:
Упрощая выражения, получаем систему уравнений
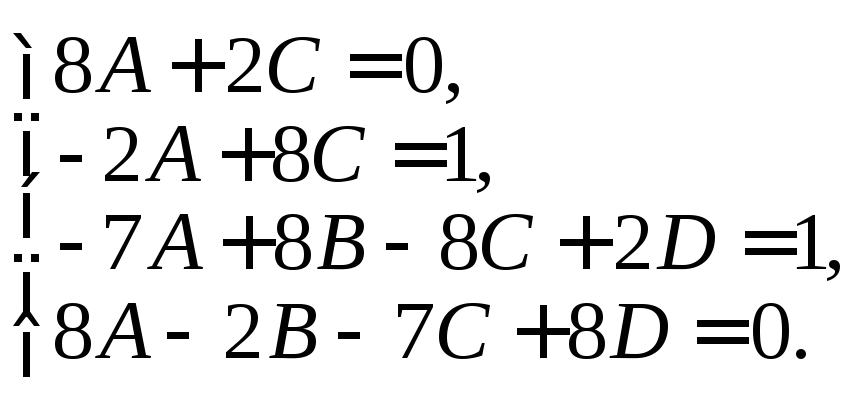
Решаем ее и находим:
Подставляем
найденные коэффициенты в
Тогда общее решение заданного дифференциального уравнения:
Пример 4. Решить уравнения:
1)
2)
3)
Решение. 1) Это линейное неоднородное уравнение 2-го порядка с постоянными коэффициентами и специальной правой частью вида
где
b
– число,
Соответствующее однородное уравнение:
Его
характеристическое уравнение
корни которого
– действительные, простые.
Тогда общее решение соответствующего однородного дифференциального уравнения:
Запишем
контрольное число
Оно не является корнем характеристического
уравнения.
Тогда частное решение заданного дифференциального уравнения ищем в виде
где A – коэффициент, который надо найти.
Дифференцируем
дважды:
Подставляем
в заданное дифференциальное уравнение:
получаем
Затем
подставляем этот коэффициент в выражение
для
Общее решение заданного дифференциального уравнения запишем в виде
2) Это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами и специальной правой частью вида
где
Соответствующее однородное уравнение имеет вид:
Его
характеристическое уравнение
корни которого
– простые комплексно-сопряженные.
Тогда общее решение однородного уравнения:
Контрольное
число
совпадает с одним из корней
характеристического уравнения, кратности
1. Поэтому частное решение заданного
дифференциального уравнения ищем в
виде
где A, B – коэффициенты, которые надо найти.
Дифференцируем
дважды:
Упрощаем
Подставляем
в заданное дифференциальное уравнение:
Группируя
относительно
а также
и приравнивая коэффициенты при одноименных
тригонометрических функциях, получим
систему
из
которой находим
Тогда частное решение:
а общее решение заданного дифференциального уравнения:
или
3)
Это линейное неоднородное дифференциальное
уравнение с постоянными коэффициентами
и специальной правой частью вида
Для нахождения его общего решения
воспользуемся методом Эйлера и теоремой
о наложении решений.
Соответствующее
однородное уравнение для заданного
дифференциального уравнения
Его характеристическое уравнение
корни которого
– простые действительные.
Общее решение однородного уравнения:
Частное решение заданного дифференциального уравнения будем искать в виде
где
– частное решение дифференциального
уравнения:
(22.71)
–частное
решение дифференциального уравнения:
(22.72)
Контрольные
числа этих дифференциальных уравнений
и
соответственно. Заметим, что
не является корнем характеристического
уравнения, значит, частное решение
ищем в виде
где A, B – коэффициенты, которые надо найти.
Дифференцируем
Подставляя
в дифференциальное уравнение (22.71)
и
получим:
откуда
находим
Тогда
Аналогично,
так как
– простой корень характеристического
уравнения, то частное решение (22.72) ищем
в виде
где С – коэффициент, который надо найти.
Дифференцируем
Подставляем
и
в (22.72):
или
Отсюда
получаем, что
Тогда
Записываем
частное решение заданного дифференциального
уравнения:
Тогда общее решение заданного
дифференциального уравнения имеет вид:
Пример 5. Решить задачу Коши:
Решение. Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами и специальной правой частью вида
где
Соответствующее
однородное дифференциальное уравнение
Его характеристическое уравнение:
корни которого
– действительные, простые. Тогда общее
решение однородного уравнения:
Контрольное
число
не является корнем характеристического
уравнения. Поэтому частное решение
заданного дифференциального уравнения
ищем в виде
где A, B – неизвестные коэффициенты.
Дифференцируем
трижды:
Подставляем
и
в заданное дифференциальное уравнение:
Приравниваем коэффициенты при одноименных тригонометрических функциях, получаем систему
из
которой находим
Тогда получаем:
Общее решение заданного дифференциального уравнения:
Дифференцируем общее решение:
Подставляем заданные начальные условия:
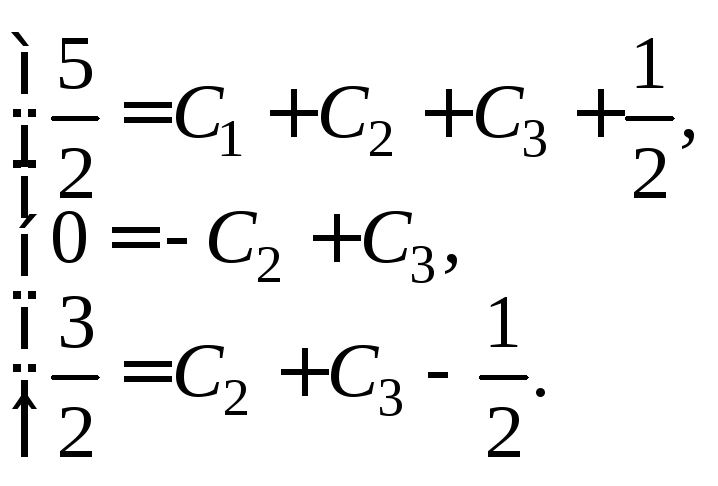
Из
полученной системы находим
Решением
задачи Коши является
Задания