20. Определенный интеграл

20.1. Понятие определенного интеграла и его свойства

Пусть на отрезке [a;b], (всюду) определена непрерывная ограниченная функцияf (x). Произвольным образом разобьем отрезок [a;b] наnотрезков точкамиПолученные отрезки…будем называть частичными. Длинуk-го частичного отрезкаобозначимНа каждом частичном отрезке выберем произвольную точку(рис. 20.1) и вычислим значение функции в этой точке, т. е.

Рис. 20.1

Для каждого k,найдем произведениеи составим сумму:

(20.1)

Сумма (20.1) называется интегральной суммойфункцииf (x) на отрезке [a;b].

Обозначим через длину наибольшего частичного отрезка.

Будем рассматривать всевозможные разбиения отрезка [a;b] при условии, чтои

Определение.Если существует предел интегральной суммы (20.1) прикоторый не зависит ни от способа разбиения отрезкана частичные отрезки, ни от выбора точекна каждом частичном отрезке, то этот предел называетсяопределенным интеграломфункцииf (x) на отрезке [a;b] и обозначается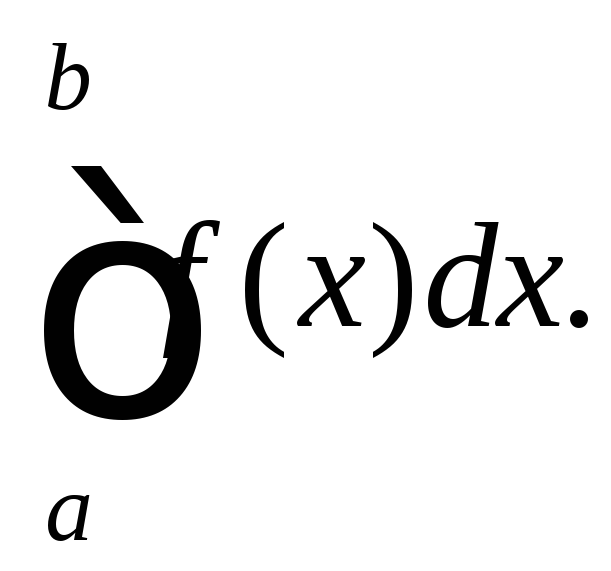

Таким образом,

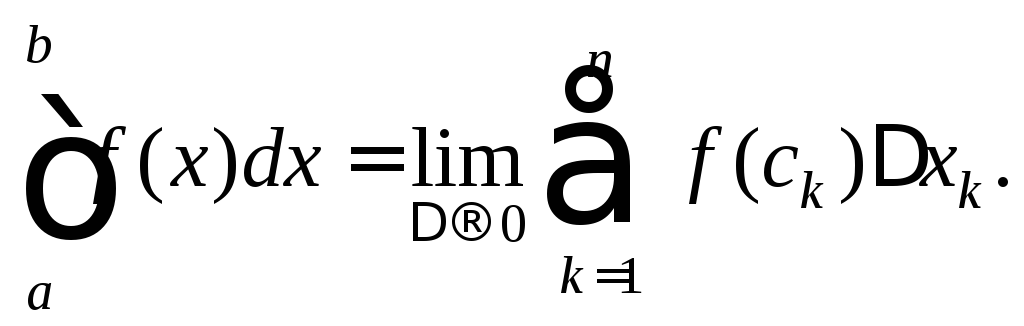(20.2)

Числа aиbв формуле (20.2) называются соответственнонижним иверхним пределами интегрирования. Функцияf (x) называетсяподынтегральной функцией,f (x)dx–подынтегральным выражением,x–переменной интегрирования, отрезок [a;b] –отрезком интегрирования.

Функция f (x), для которой существует интеграл (20.2), называетсяинтегрируемой на отрезке.

Классы интегрируемых функций:

1) непрерывная на отрезке [a;b] функция интегрируема;

2) ограниченная на отрезке [a;b] функция, имеющая лишь конечное число точек разрыва, интегрируема;

3) монотонная ограниченная функция интегрируема.

Если то фигура, ограниченная графиком функцииосьюOx, прямымииназываетсякриволинейной трапецией (рис. 20.1).

Геометрический смысл определенного интеграла: определенный интеграл (20.2) от неотрицательной функции численно равен площади криволинейной трапеции.

Физический смысл определенного интеграла: пусть материальная точкаMдвижется вдоль числовой оси со скоростьюV(t),Тогда путь, пройденный точкой за промежуток времени отдоравен определенному интегралу от скорости:

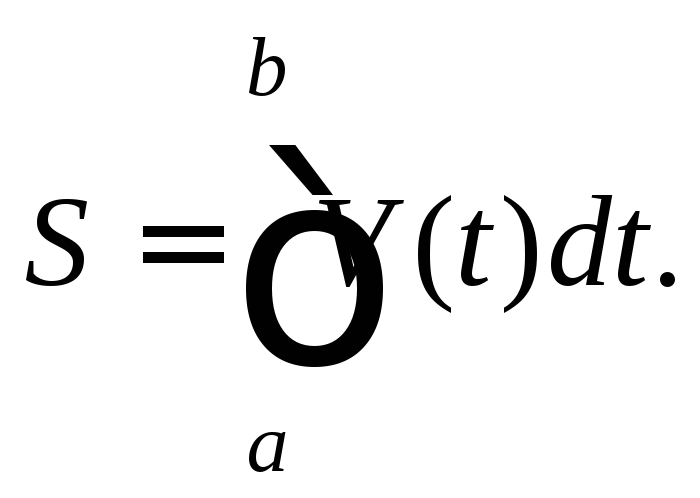
Свойства определенного интеграла

1)

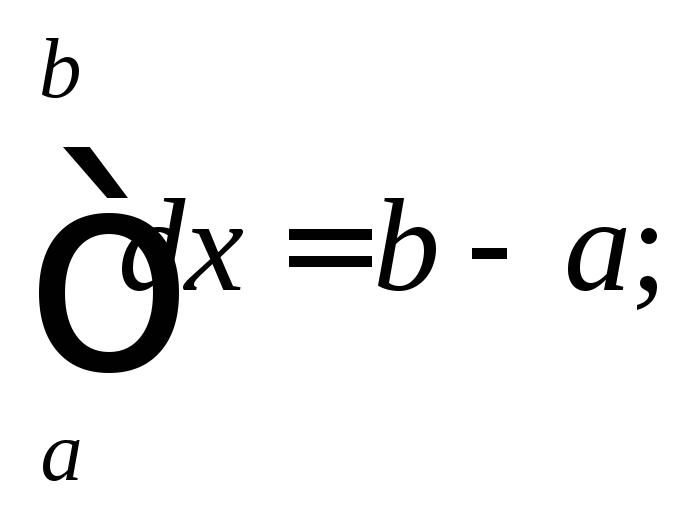
2)

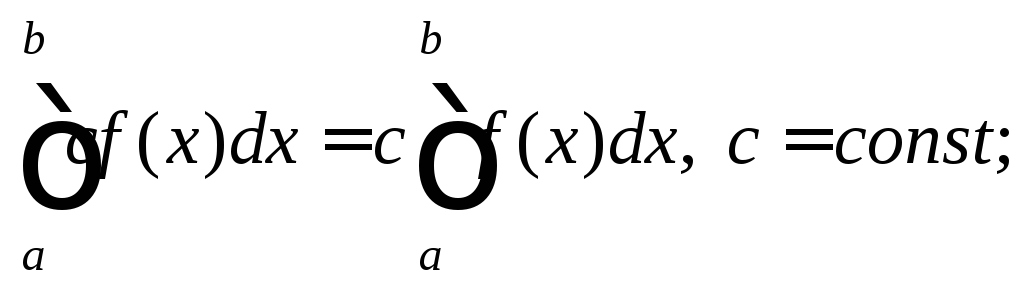
3)

равенства 2 и 3 в совокупности называются свойством линейности;

4)

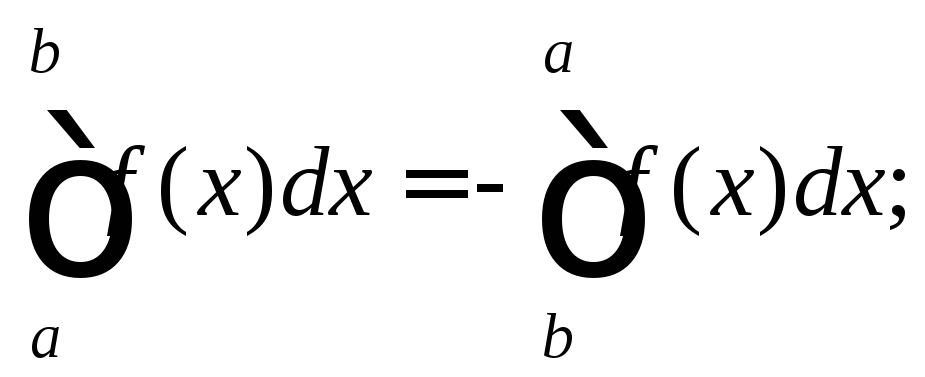
5)

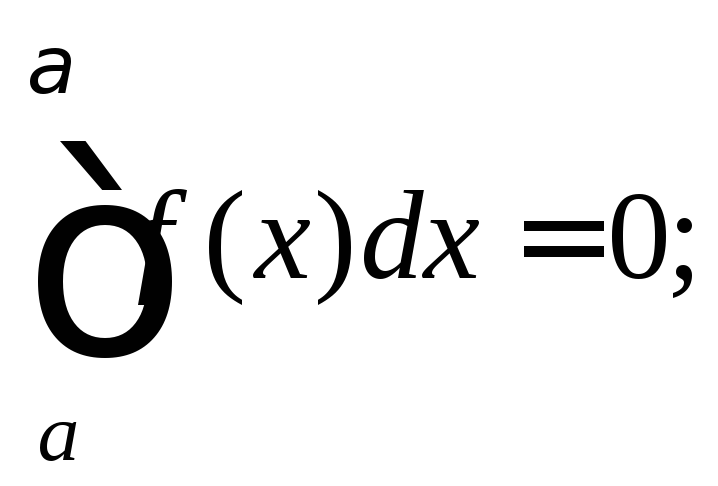
6) значение интеграла не зависит от обозначения переменной интегрирования:

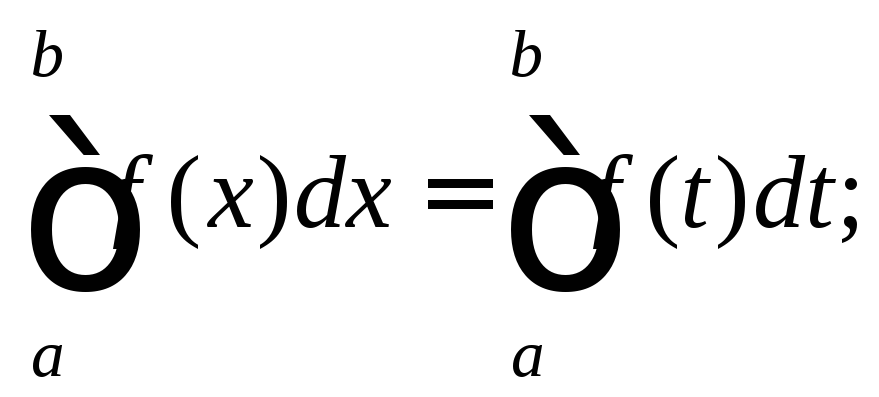
7) свойство аддитивности: при любом взаимном расположении чиселa,b,cимеет место формула:

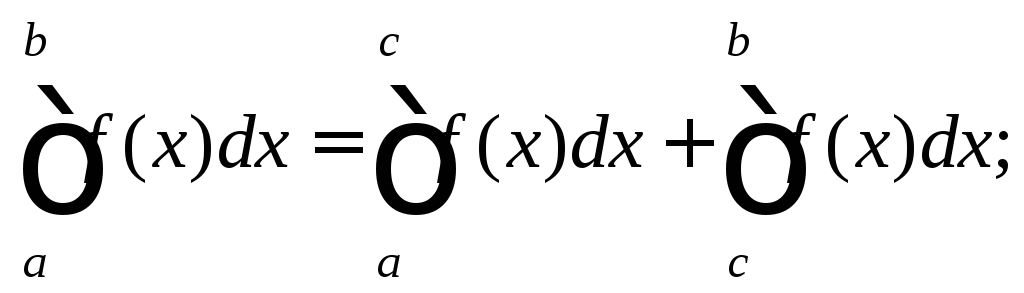
8) если прито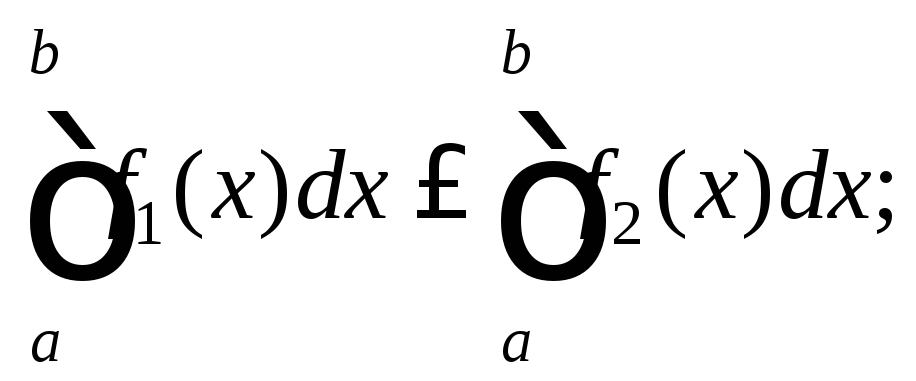

9) если mиM– соответственно наименьшее и наибольшее значения функциина отрезке [a;b], то верна оценка

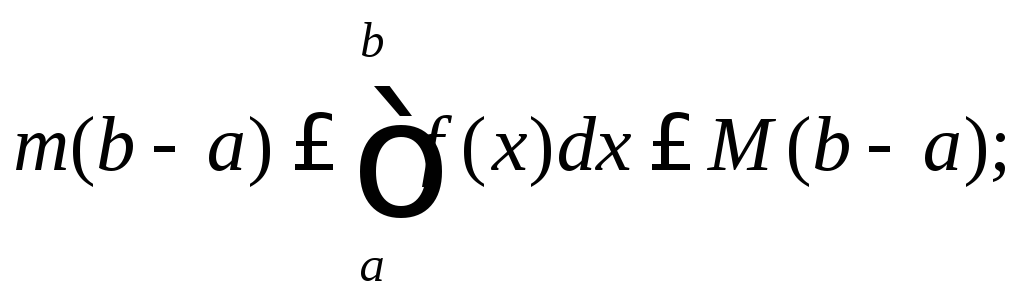
10)

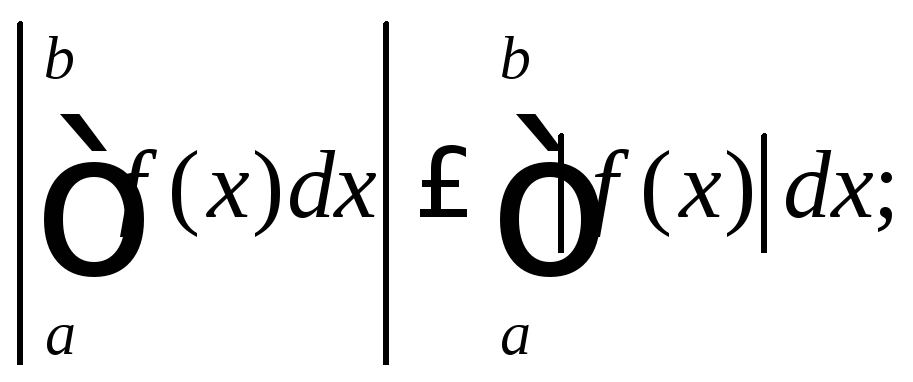
11) если функция f (x) непрерывна на отрезке [a;b], то существует точкатакая, что

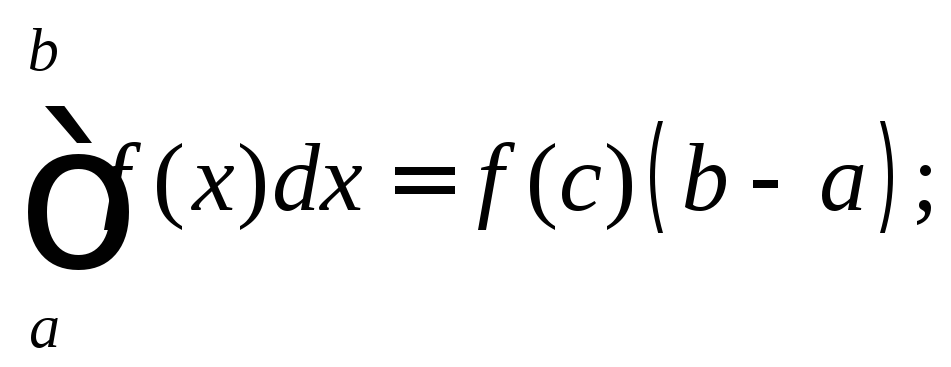
12) если f (x) – нечетная функция, то

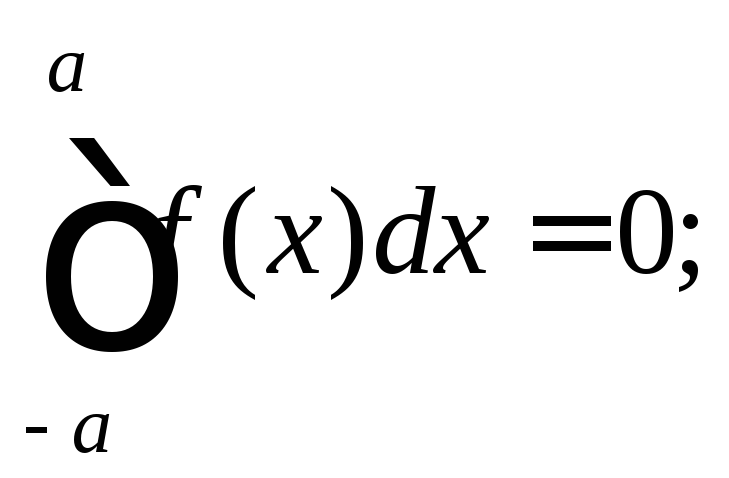
13) если f (x) – четная функция, то

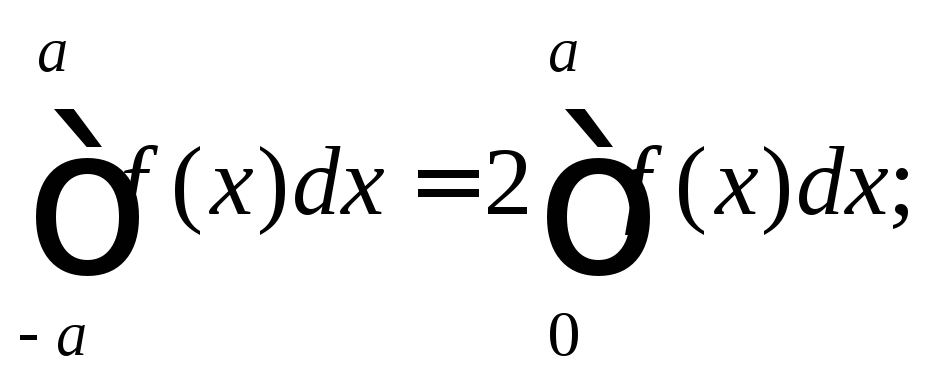
14) если f (x) – периодическая функция периодаT, то при любомверно равенство

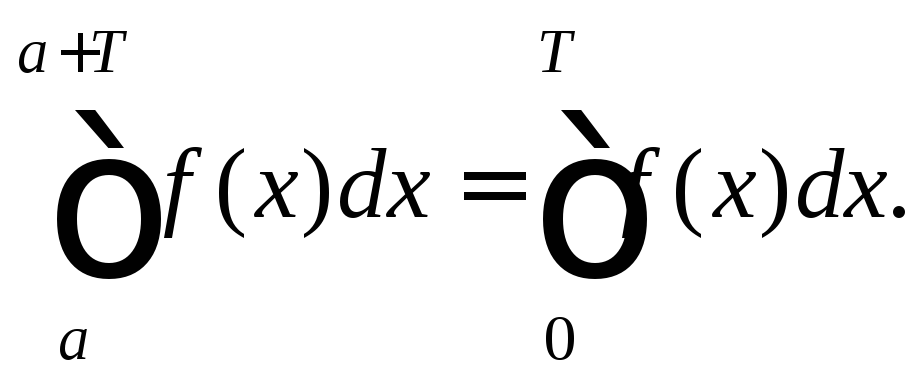
Предполагается, что все интегралы, приведенные в свойствах 1–14, существуют.

Пример 1. Вычислить по определению интеграл

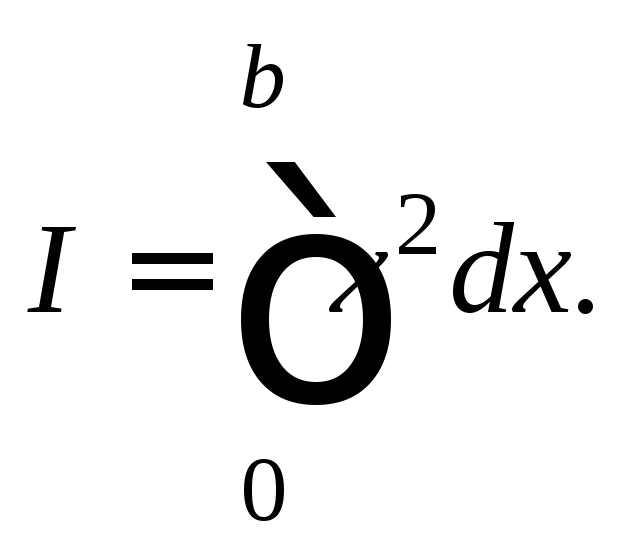
Решение. Функция интегрируема на отрезке [0;b], поскольку она непрерывна. Разобьем отрезок [0;b] на n частей точками где

В качестве точек возьмем крайние правые точки каждого частичного отрезкат. е.

Вычислим значения функции

Составим интегральную сумму

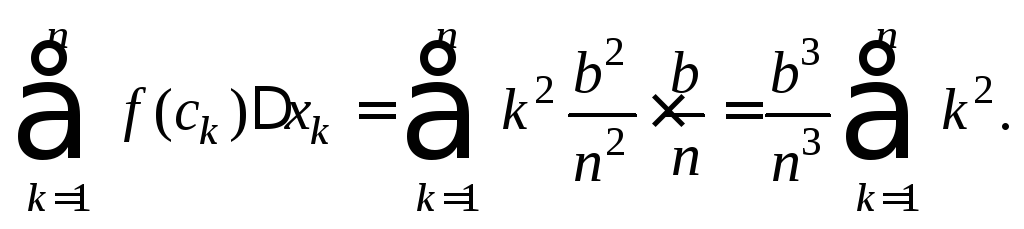
Методом математической индукции можно доказать, что

Тогда получаем:

Имеем:

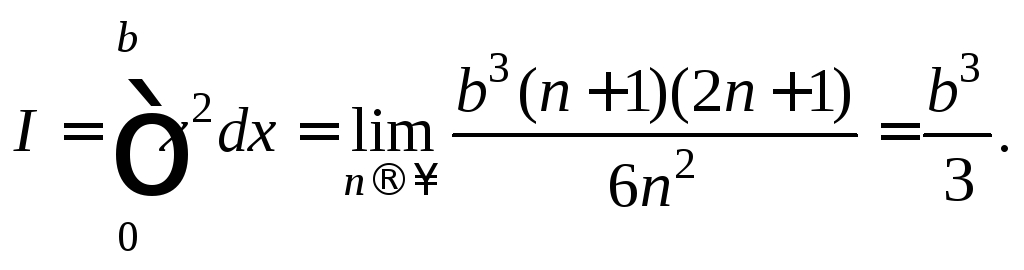
Пример 2. Доказать, что функция Дирихле

не интегрируема на отрезке [0; 1].

Решение. Разобьем отрезок [0; 1] произвольным образом на n частичных отрезков. При составлении интегральной суммы выберем в качестве точек рациональные числа. Тогда

Получаем:

Затем составим интегральную сумму, выбрав в качестве точек иррациональны числа. ТогдаПолучаем:

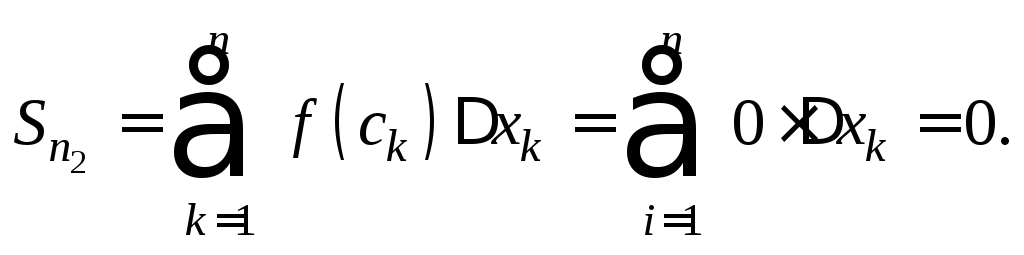
Таким образом, интегральные суммы могут принимать как значение, равное 1, так и значение, равное 0. Следовательно, предел интегральных сумм не существует, т. е. функция Дирихле не интегрируема на отрезке [0; 1], хотя и ограничена на всей числовой прямой.

Пример 3. Сравнить интегралы и

Решение. Так как при(рис. 20.2), то по свойству сравнения определенных интегралов (см. 8-е свойство) имеем:

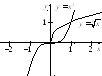
Рис. 20.2

Пример 4. Доказать неравенство

Решение. Так как прито по 9-му свойству определенных интегралов имеем:

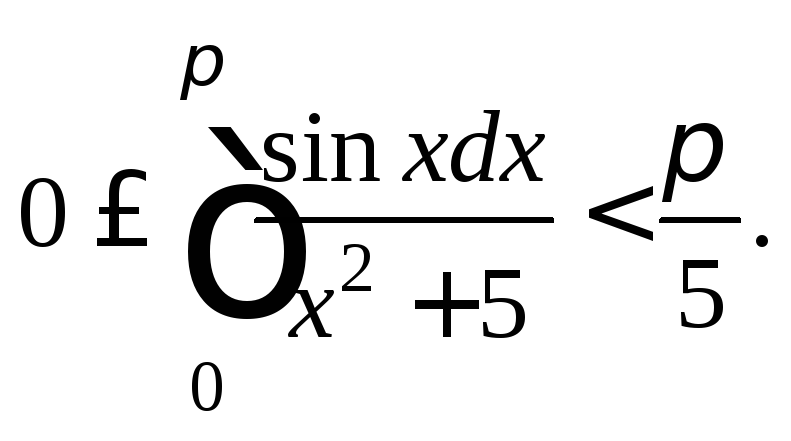
Пример 5. Оценить интеграл

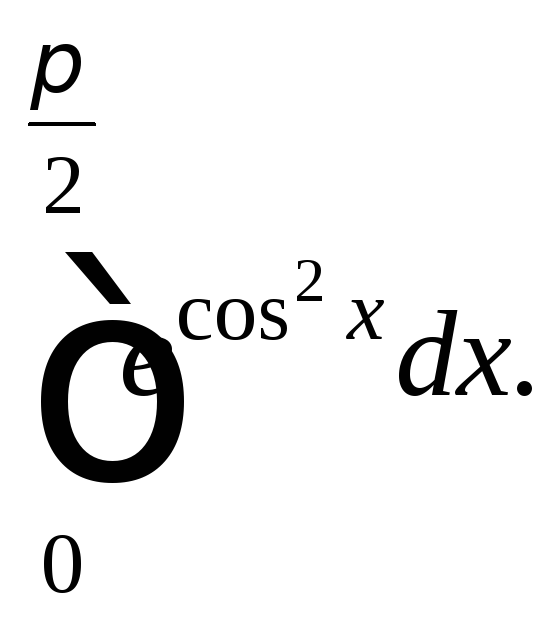
Решение. Так как притоТогда по 8-му свойству определенных интегралов получаем:

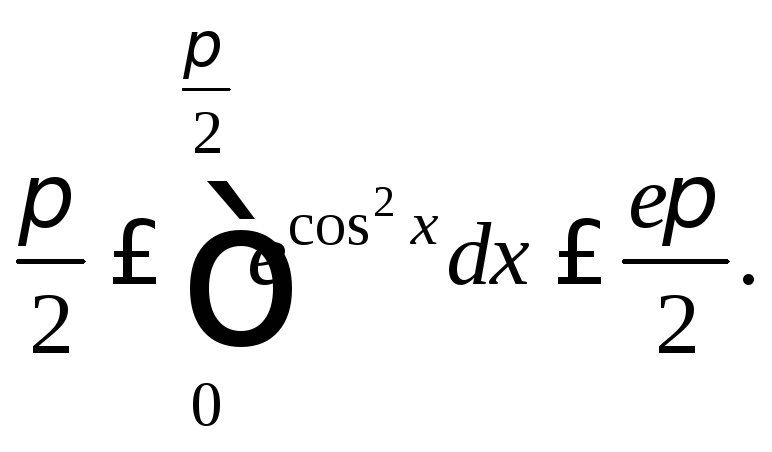
Пример 6. Вычислить определенный интеграл:

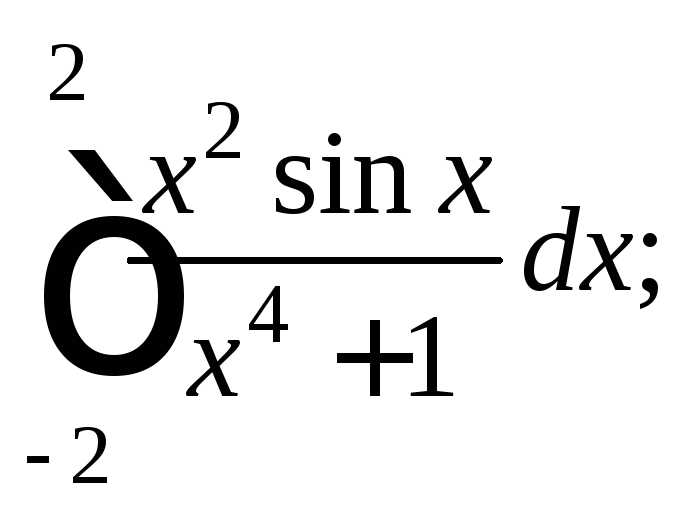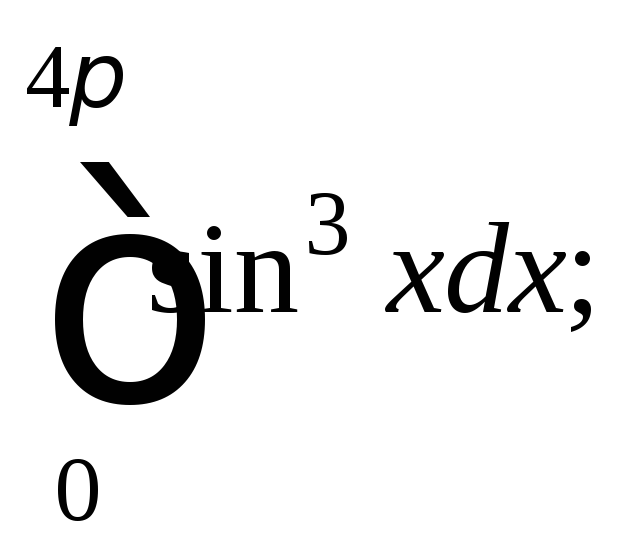1) 2)3)

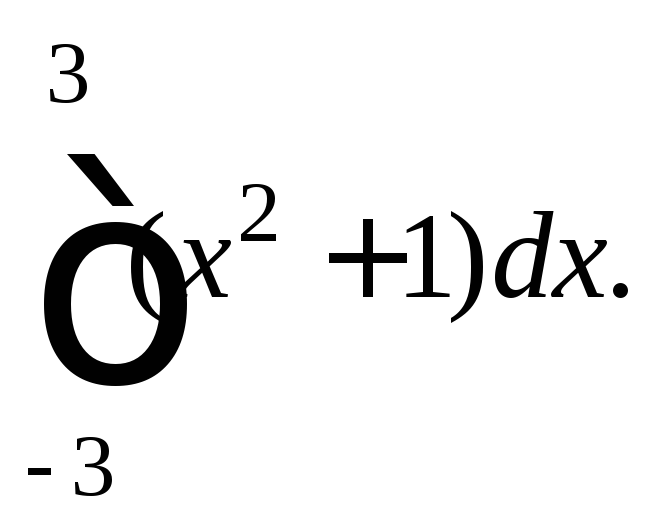
Решение. 1) Так как подынтегральная функция является нечетной, а отрезок интегрирования симметричен относительно начала координат, то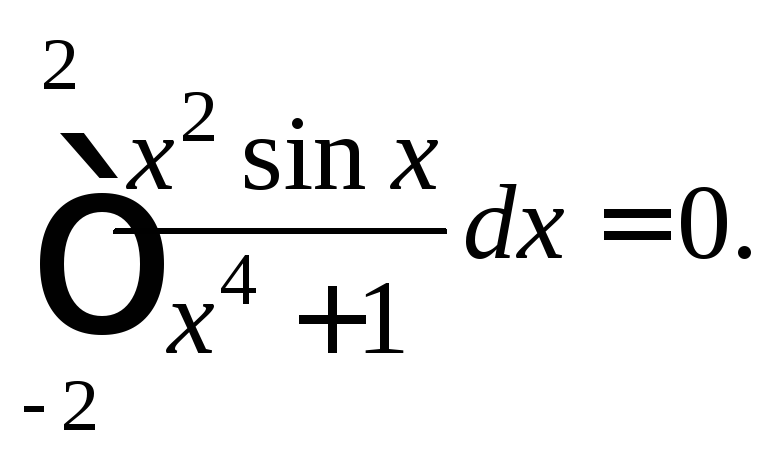

2) Функция является периодической с периодомИспользуем 7-е и 14-е свойства интеграла:

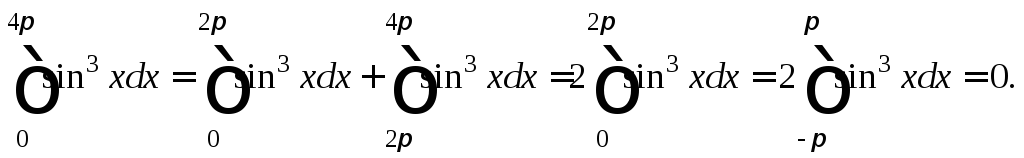
Последний интеграл равен нулю в силу нечетности функции

3) Функция является четной, а отрезок интегрирования симметричен относительно начала координат, поэтому

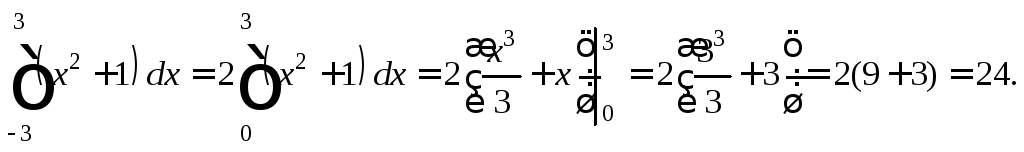
Задания